Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T20:56:13.287Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall-bounded thermal turbulent convection driven by heat-releasing point particles

Published online by Cambridge University Press:  15 December 2022

Yuhang Du  and
Yantao Yang Open the ORCID record for Yantao Yang [Opens in a new window]
Yuhang Du
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, and Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China Joint Laboratory of Marine Hydrodynamics and Ocean Engineering, Pilot National Laboratory for Marine Science and Technology (Qingdao), Shandong 266299, PR China
Yantao Yang*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, and Department of Mechanics and Engineering Science, College of Engineering, Peking University, Beijing 100871, PR China Joint Laboratory of Marine Hydrodynamics and Ocean Engineering, Pilot National Laboratory for Marine Science and Technology (Qingdao), Shandong 266299, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

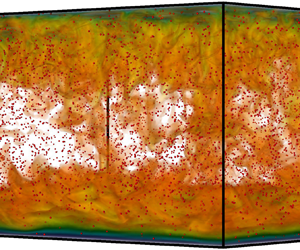
In this work we investigate the thermal convection driven by heat-releasing point particles. Three-dimensional direct numerical simulations are conducted for $1\times 10^7\le {\textit {Ra}} \le 1\times 10^{10}$ and $0.01\le {\textit {St}} \le 10$, where the Rayleigh number ${\textit {Ra}}$ and Stokes number ${\textit {St}}$ measure the strengths of the heat releasing rate and the Stokes drag, respectively. A regime at intermediate Stokes numbers is identified with most particles accumulating into the top boundary layer region, while for other cases particles are constantly advected over the entire domain. For the latter state, the flow motions are stronger at the upper part of the domain. The thicknesses of both momentum and thermal boundary layers at the top plate follow the same scaling law with ${\textit {Ra}}$ and show minor dependences on ${\textit {St}}$. The volume-averaged temperature and convective flux exhibit non-monotonic variations as ${\textit {St}}$ increases and reach their minimums at intermediate ${\textit {St}}$. The fraction coefficient of heat flux, i.e. the ratio between the heat flux through the bottom plate and the total flux through both plates, shares the similar dependence on ${\textit {St}}$ as the convective flux. The relation between these scaling laws can be explained by using the global balance between the dissipation and convective flux. The scaling laws for the transition between different flow regimes are also proposed and agree with the numerical results. The preferential concentration of particles is observed for all cases and is strongest at intermediate Stokes numbers, for which multiscale clustering emerges with small clusters forming larger ones.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 953 , 25 December 2022 , A41
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Balachandar, S. & Eaton, J.K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133.CrossRefGoogle Scholar
Banko, A.J., Villafañe, L., Kim, J.H. & Eaton, J.K. 2020 Temperature statistics in a radiatively heated particle-laden turbulent square duct flow. Intl J. Heat Fluid Flow 84, 108618.CrossRefGoogle Scholar
Bouillaut, V., Lepot, S., Aumaître, S. & Gallet, B. 2019 Transition to the ultimate regime in a radiatively driven convection experiment. J. Fluid Mech. 861, R5.CrossRefGoogle Scholar
Creyssels, M. 2020 Model for classical and ultimate regimes of radiatively driven turbulent convection. J. Fluid Mech. 900, A39.CrossRefGoogle Scholar
Crowe, C.T. 1982 Review – numerical models for dilute gas-particle flows. J. Fluids Engng 104 (3), 297–303.CrossRefGoogle Scholar
Cuzzi, J.N., Hogan, R.C., Paque, J.M. & Dobrovolskis, A.R. 2001 Size-selective concentration of chondrules and other small particles in protoplanetary nebula turbulence. Astrophys. J. 546 (1), 496.CrossRefGoogle Scholar
Dritselis, C.D. & Vlachos, N.S. 2011 Large eddy simulation of gas-particle turbulent channel flow with momentum exchange between the phases. Intl J. Multiphase Flow 37 (7), 706–721.CrossRefGoogle Scholar
Du, Y., Zhang, M. & Yang, Y. 2021 Two-component convection flow driven by a heat-releasing concentration field. J. Fluid Mech. 929, A35.CrossRefGoogle Scholar
Du, Y., Zhang, M. & Yang, Y. 2022 Thermal convection driven by a heat-releasing scalar component. Acta Mechanica Sin. 38 (10), 321584.CrossRefGoogle Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.CrossRefGoogle Scholar
Ferenc, J. & Néda, Z. 2007 On the size distribution of Poisson Voronoï cells. Phys. A 385 (2), 518–526.CrossRefGoogle Scholar
Frankel, A., Pouransari, H., Coletti, F. & Mani, A. 2016 Settling of heated particles in homogeneous turbulence. J. Fluid Mech. 792, 869–893.CrossRefGoogle Scholar
Goluskin, D. & van der Poel, E.P. 2016 Penetrative internally heated convection in two and three dimensions. J. Fluid Mech. 791, R6.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86 (15), 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66 (1 Pt 2), 016305.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16 (12), 4462–4472.CrossRefGoogle Scholar
Ireland, P.J., Bragg, A.D. & Collins, L.R. 2016 The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.CrossRefGoogle Scholar
Jiang, K., Du, X., Kong, Y., Xu, C. & Ju, X. 2019 A comprehensive review on solid particle receivers of concentrated solar power. Renew. Sustain. Energy Rev. 116, 109463.CrossRefGoogle Scholar
Kazemi, S., Ostilla-Mónico, R. & Goluskin, D. 2022 Transition between boundary-limited scaling and mixing-length scaling of turbulent transport in internally heated convection. Phys. Rev. Lett. 129, 024501.CrossRefGoogle ScholarPubMed
Kuerten, J.G.M., van der Geld, C.W.M. & Geurts, B.J. 2011 Turbulence modification and heat transfer enhancement by inertial particles in turbulent channel flow. Phys. Fluids 23 (12), 123301.CrossRefGoogle Scholar
Lepot, S., Aumaitre, S. & Gallet, B. 2018 Radiative heating achieves the ultimate regime of thermal convection. Proc. Natl Acad. Sci. USA 115 (36), 8937–8941.CrossRefGoogle ScholarPubMed
Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22 (10), 103304.CrossRefGoogle Scholar
Oresta, P. & Prosperetti, A. 2013 Effects of particle settling on Rayleigh–Bénard convection. Phys. Rev. E 87 (6), 063014.CrossRefGoogle ScholarPubMed
Ostilla-Monico, R., Yang, Y., van der Poel, E.P., Lohse, D. & Verzicco, R. 2015 A multiple-resolution strategy for direct numerical simulation of scalar turbulence. J. Comput. Phys. 301, 308–321.CrossRefGoogle Scholar
Pan, M., Dong, Y., Zhou, Q. & Shen, L. 2022 Flow modulation and heat transport of radiatively heated particles settling in Rayleigh–Bénard convection. Comput. Fluids 241, 105454.CrossRefGoogle Scholar
Park, H.J., O'Keefe, K. & Richter, D.H. 2018 Rayleigh–Bénard turbulence modified by two-way coupled inertial, nonisothermal particles. Phys. Rev. Fluids 3 (3), 034307.CrossRefGoogle Scholar
Pouransari, H. & Mani, A. 2017 Effects of preferential concentration on heat transfer in particle-based solar receivers. J. Sol. Energy Engng 139 (2), 021008.CrossRefGoogle Scholar
Roberts, P.H. 1967 Convection in horizontal layers with internal heat generation. Theory. J. Fluid Mech. 30 (1), 33–49.CrossRefGoogle Scholar
Sardina, G., Schlatter, P., Brandt, L., Picano, F. & Casciola, C.M. 2012 Wall accumulation and spatial localization in particle-laden wall flows. J. Fluid Mech. 699, 50–78.CrossRefGoogle Scholar
Shaw, R.A. 2003 Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35 (1), 183–227.CrossRefGoogle Scholar
Shotorban, B., Mashayek, F. & Pandya, R.V.R. 2003 Temperature statistics in particle-laden turbulent homogeneous shear flow. Intl J. Multiphase Flow 29 (8), 1333–1353.CrossRefGoogle Scholar
Shraiman, B.I. & Siggia, E.D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
Sun, C., Cheung, Y.H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Van Heerden, C., Nobel, A.P.P. & Van Krevelen, D.W. 1953 Mechanism of heat transfer in fluidized beds. Ind. Engng Chem. 45 (6), 1237–1242.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flows in cylindrical coordinates. J. Comput. Phys. 123 (2), 402–414.CrossRefGoogle Scholar
Wang, Q., Lohse, D. & Shishkina, O. 2020 Scaling in internally heated convection: a unifying theory. Geophys. Res. Lett. 48, e2020GL091198.Google Scholar
Yang, W., Zhang, Y.-Z., Wang, B.-F., Dong, Y. & Zhou, Q. 2021 Dynamic coupling between carrier and dispersed phases in Rayleigh–Bénard convection laden with inertial isothermal particles. J. Fluid Mech. 930, A24.CrossRefGoogle Scholar
Zamansky, R., Coletti, F., Massot, M. & Mani, A. 2014 Radiation induces turbulence in particle-laden fluids. Phys. Fluids 26 (7), 071701.CrossRefGoogle Scholar
Zamansky, R., Coletti, F., Massot, M. & Mani, A. 2016 Turbulent thermal convection driven by heated inertial particles. J. Fluid Mech. 809, 390–437.CrossRefGoogle Scholar