Article contents
Wall-attached structures of velocity fluctuations in a turbulent boundary layer
Published online by Cambridge University Press: 12 October 2018
Abstract
Wall turbulence is a ubiquitous phenomenon in nature and engineering applications, yet predicting such turbulence is difficult due to its complexity. High-Reynolds-number turbulence arises in most practical flows, and is particularly complicated because of its wide range of scales. Although the attached-eddy hypothesis postulated by Townsend can be used to predict turbulence intensities and serves as a unified theory for the asymptotic behaviours of turbulence, the presence of coherent structures that contribute to the logarithmic behaviours has not been observed in instantaneous flow fields. Here, we demonstrate the logarithmic region of the turbulence intensity by identifying wall-attached structures of the velocity fluctuations (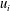 $u_{i}$) through the direct numerical simulation of a moderate-Reynolds-number boundary layer (
$u_{i}$) through the direct numerical simulation of a moderate-Reynolds-number boundary layer (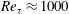 $Re_{\unicode[STIX]{x1D70F}}\approx 1000$). The wall-attached structures are self-similar with respect to their heights (
$Re_{\unicode[STIX]{x1D70F}}\approx 1000$). The wall-attached structures are self-similar with respect to their heights (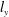 $l_{y}$), and in particular the population density of the streamwise component (
$l_{y}$), and in particular the population density of the streamwise component ( $u$) scales inversely with
$u$) scales inversely with 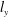 $l_{y}$, reminiscent of the hierarchy of attached eddies. The turbulence intensities contained within the wall-parallel components (
$l_{y}$, reminiscent of the hierarchy of attached eddies. The turbulence intensities contained within the wall-parallel components ( $u$ and
$u$ and 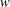 $w$) exhibit the logarithmic behaviour. The tall attached structures (
$w$) exhibit the logarithmic behaviour. The tall attached structures (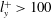 $l_{y}^{+}>100$) of
$l_{y}^{+}>100$) of  $u$ are composed of multiple uniform momentum zones (UMZs) with long streamwise extents, whereas those of the cross-stream components (
$u$ are composed of multiple uniform momentum zones (UMZs) with long streamwise extents, whereas those of the cross-stream components ( $v$ and
$v$ and 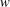 $w$) are relatively short with a comparable width, suggesting the presence of tall vortical structures associated with multiple UMZs. The magnitude of the near-wall peak observed in the streamwise turbulent intensity increases with increasing
$w$) are relatively short with a comparable width, suggesting the presence of tall vortical structures associated with multiple UMZs. The magnitude of the near-wall peak observed in the streamwise turbulent intensity increases with increasing 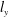 $l_{y}$, reflecting the nested hierarchies of the attached
$l_{y}$, reflecting the nested hierarchies of the attached  $u$ structures. These findings suggest that the identified structures are prime candidates for Townsend’s attached-eddy hypothesis and that they can serve as cornerstones for understanding the multiscale phenomena of high-Reynolds-number boundary layers.
$u$ structures. These findings suggest that the identified structures are prime candidates for Townsend’s attached-eddy hypothesis and that they can serve as cornerstones for understanding the multiscale phenomena of high-Reynolds-number boundary layers.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 103
- Cited by



