Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T01:59:09.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall to wall optimal transport

Published online by Cambridge University Press:  24 June 2014

Pedram Hassanzadeh ,
Gregory P. Chini  and
Charles R. Doering
Pedram Hassanzadeh
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
Gregory P. Chini
Affiliation:
Department of Mechanical Engineering, Program in Integrated Applied Mathematics and Center for Fluid Physics, University of New Hampshire, Durham, NH 03824, USA
Charles R. Doering*
Affiliation:
Department of Mathematics, Department of Physics and Center for the Study of Complex Systems, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The calculus of variations is employed to find steady divergence-free velocity fields that maximize transport of a tracer between two parallel walls held at fixed concentration for one of two constraints on flow strength: a fixed value of the kinetic energy (mean square velocity) or a fixed value of the enstrophy (mean square vorticity). The optimizing flows consist of an array of (convection) cells of a particular aspect ratio 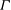$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\varGamma $. We solve the nonlinear Euler–Lagrange equations analytically for weak flows and numerically – as well as via matched asymptotic analysis in the fixed energy case – for strong flows. We report the results in terms of the Nusselt number 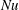${\mathit{Nu}}$, a dimensionless measure of the tracer transport, as a function of the Péclet number 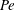${\mathit{Pe}}$, a dimensionless measure of the strength of the flow. For both constraints, the maximum transport 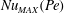${\mathit{Nu}}_{\mathit{MAX}}({\mathit{Pe}})$ is realized in cells of decreasing aspect ratio 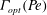$\varGamma _{\mathit{opt}}({\mathit{Pe}})$ as 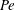${\mathit{Pe}}$ increases. For the fixed energy problem, 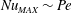${\mathit{Nu}}_{\mathit{MAX}} \sim {\mathit{Pe}}$ and 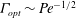$\varGamma _{\mathit{opt}} \sim {\mathit{Pe}}^{-1/2}$, while for the fixed enstrophy scenario, 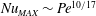${\mathit{Nu}}_{\mathit{MAX}} \sim {\mathit{Pe}}^{10/17}$ and 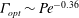$\varGamma _{\mathit{opt}} \sim {\mathit{Pe}}^{-0.36}$. We interpret our results in the context of buoyancy-driven Rayleigh–Bénard convection problems that satisfy the flow intensity constraints, enabling us to investigate how the transport scalings compare with upper bounds on 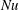${\mathit{Nu}}$ expressed as a function of the Rayleigh number 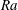${\mathit{Ra}}$. For steady convection in porous media, corresponding to the fixed energy problem, we find 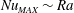${\mathit{Nu}}_{\mathit{MAX}} \sim {\mathit{Ra}}$ and 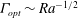$\varGamma _{\mathit{opt}} \sim {\mathit{Ra}}^{-1/2}$, while for steady convection in a pure fluid layer between stress-free isothermal walls, corresponding to fixed enstrophy transport, 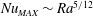${\mathit{Nu}}_{\mathit{MAX}} \sim {\mathit{Ra}}^{5/12}$ and 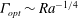$\varGamma _{\mathit{opt}} \sim {\mathit{Ra}}^{-1/4}$.

JFM classification

Convection: Convection in porous media Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 627 - 662
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Centre for the Environment and Department of Earth and Planetary Sciences, Harvard University, Cambridge, MA 02139, USA.

References

Boyd, J. P. 2001 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover.Google Scholar
Busse, F. H. 1969 On Howard’s bound for heat transport by turbulent convection. J. Fluid Mech. 37, 457–477.Google Scholar
Busse, F. H. 1970 Bounds for turbulent shear flow. J. Fluid Mech. 41, 219–240.CrossRefGoogle Scholar
Busse, F. H. & Joseph, D. D. 1972 Bounds for heat transport in a porous layer. J. Fluid Mech. 54, 521–543.Google Scholar
Caulfield, C. P. & Kerswell, R. R. 2001 Maximal mixing rate in turbulent stably stratified Couette flow. Phys. Fluids 13, 894–900.CrossRefGoogle Scholar
Cheskidov, A., Petrov, N. P. & Doering, C. R. 2007 Energy dissipation in fractal-forced flow. J. Math. Phys. 48, 065208.Google Scholar
Chini, G. P. & Cox, S. M. 2009 Large Rayleigh number thermal convection: heat flux predictions and strongly nonlinear solutions. Phys. Fluids 21 (8), 083603.CrossRefGoogle Scholar
Corson, L. T.2011 Maximizing the heat flux in steady unicellular porous media convection. Tech. Rep., Geophysical Fluid Dynamics Program. Woods Hole Oceanographic Institution.Google Scholar
Cortelezzi, L., Adrover, A. & Giona, M. 2008 Feasibility, efficiency and transportability of short horizon optimal mixing protocols. J. Fluid Mech. 597, 199–231.Google Scholar
D’Alessandro, D., Dahleh, M. & Mezic, I. 1999 Control of mixing in fluid flow: a maximum entropy approach. IEEE Trans. Autom. Control 44 (10), 1852–1863.Google Scholar
Doering, C. R. & Constantin, P. 1992 Energy dissipation in shear driven turbulence. Phys. Rev. Lett. 69, 1648–1651.Google Scholar
Doering, C. R. & Constantin, P. 1994 Variational bounds on energy dissipation in incompressible flows: shear flow. Phys. Rev. E 49, 4087–4099.Google Scholar
Doering, C. R. & Constantin, P. 1996 Variational bounds on energy dissipation in incompressible flows. III. Convection. Phys. Rev. E 53, 5957–5981.Google Scholar
Doering, C. R. & Constantin, P. 1998 Bounds for heat transport in a porous layer. J. Fluid Mech. 376, 263–296.Google Scholar
Doering, C. R., Eckhardt, B. & Schumacher, J. 2003 Energy dissipation in body-forced plane shear flow. J. Fluid Mech. 494, 275–284.Google Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.Google Scholar
Doering, C. R., Otto, F. & Reznikoff, M. G. 2006 Bounds on vertical heat transport for infinite-Prandtl-number Rayleigh–Bénard convection. J. Fluid Mech. 560, 229–241.Google Scholar
Doering, C. R., Spiegel, E. A. & Worthing, R. A. 2000 Energy dissipation in a shear layer with suction. Phys. Fluids 12, 1955–1968.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Fowler, A. C. 1997 Mathematical Models in the Applied Sciences. Cambridge University Press.Google Scholar
Gubanov, O. & Cortelezzi, L. 2010 Towards the design of an optimal mixer. J. Fluid Mech. 651, 27–53.Google Scholar
Gubanov, O. & Cortelezzi, L. 2012 On the cost efficiency of mixing optimization. J. Fluid Mech. 692, 112–136.Google Scholar
Gupta, V. P. & Joseph, D. D. 1973 Bounds for heat transport in a porous layer. J. Fluid Mech. 57, 491–514.Google Scholar
Hagstrom, G. & Doering, C. R. 2010 Bounds on heat transport in Bénard–Marangoni convection. Phys. Rev. E 81, 047301.CrossRefGoogle ScholarPubMed
Hagstrom, G. I. & Doering, C. R. 2014 Bounds on surface stress-driven shear flow. J. Nonlinear Sci. 24, 185–199.Google Scholar
Hassanzadeh, P.2012 Optimal transport from wall to wall. Master’s thesis, University of California, Berkeley.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108 (22), 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Stability of columnar convection in a porous medium. J. Fluid Mech. 737, 205–231.Google Scholar
Horne, R. N. & O’Sullivan, P. 1978 Origin of oscillatory convection in a porous medium heated from below. Phys. Fluids 21, 1260–1264.Google Scholar
Howard, L. N. 1963 Heat transport by turbulent convection. J. Fluid Mech. 17, 405–432.Google Scholar
Howard, L.1964 Convection at high Rayleigh numbers. In Proceedings of the 11th International Congress of Applied Mechanics (ed. H. Görtler) pp. 1109–1115. Springer.Google Scholar
Ierley, G. R., Kerswell, R. R. & Plasting, S. C. 2006 Infinite-Prandtl-number convection. Part 2. A singular limit of upper bound theory. J. Fluid Mech. 560, 159–228.Google Scholar
Kerswell, R. R. 1996 Upper bounds on the energy dissipation in turbulent precession. J. Fluid Mech. 321, 335–370.Google Scholar
Kerswell, R. R. 1998 Unification of variational principles for turbulent shear flows: the background method of Doering–Constantin and the mean-fluctuation formulation of Howard–Busse. Physica D 121, 175–192.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5, 1374–1389.Google Scholar
Krommes, J. A. & Smith, R. A. 1987 Rigorous upper bounds for transport due to passive advection by inhomogeneous turbulence. Ann. Phys. 177, 246–329.CrossRefGoogle Scholar
Lin, Z., Thiffeault, J.-L. & Doering, C. R. 2011 Optimal stirring strategies for passive scalar mixing. J. Fluid Mech. 675, 465–476.Google Scholar
Malkus, W. V. R. 1954 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. Ser. A 225, 196–212.Google Scholar
Mathew, G., Mezic, I., Grivopoulos, S., Vaidya, U. & Petzold, L. 2007 Optimal control of mixing in Stokes fluid flows. J. Fluid Mech. 580, 261–281.Google Scholar
Nickerson, E. C. 1969 Upper bounds on torque in cylindrical Couette flow. J. Fluid Mech. 38, 807–815.Google Scholar
Okabe, T., Eckhardt, B., Thiffeault, J.-L. & Doering, C. R. 2008 Mixing effectiveness depends on the source-sink structure: simulation results. J. Stat. Mech. Theor. Exp. 07, P07018.Google Scholar
Otero, J.2002. Bounds for the heat transport in turbulent convection. PhD thesis, University of Michigan, Ann Arbor.Google Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.Google Scholar
Petrov, N. P., Lu, L. & Doering, C. R. 2005 Variational bounds on the energy dissipation rate in body-forced shear flow. J. Turbul. 6, 17.Google Scholar
Plasting, S. C. & Kerswell, R. R. 2003 Improved upper bound on the energy dissipation rate in plane Couette flow: the full solution to Busse’s problem and the Constantin–Doering–Hopf problem with one-dimensional background field. J. Fluid Mech. 477, 363–379.Google Scholar
Plasting, S. C. & Young, W. R. 2006 A bound on scalar variance for the advection–diffusion equation. J. Fluid Mech. 552, 289–298.Google Scholar
Rayleigh, L. 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.Google Scholar
Rollin, B., Dubief, Y. & Doering, C. R. 2011 Variations on Kolmogorov flow: turbulent energy dissipation and mean flow profiles. J. Fluid Mech. 670, 204–213.Google Scholar
Shaw, T. A., Thiffeault, J.-L. & Doering, C. R. 2007 Stirring up trouble: multi-scale mixing measures for steady scalar sources. Physica D 231, 143–164.Google Scholar
Siggers, J. H., Kerswell, R. R. & Balmforth, N. J. 2004 Bounds on horizontal convection. J. Fluid Mech. 517, 55–70.Google Scholar
Spiegel, E. A. 1962 Thermal turbulence at very small Prandtl number. J. Geophys. Res. 67, 3063–3070.CrossRefGoogle Scholar
Tang, W., Caulfield, C. P. & Kerswell, R. R. 2009 A prediction for the optimal stratification for turbulent mixing. J. Fluid Mech. 634, 487–497.Google Scholar
Tang, W., Caulfield, C. P. & Young, W. R. 2004 Bounds on dissipation in stress driven flow. J. Fluid Mech. 510, 333–352.Google Scholar
Thiffeault, J.-L., Doering, C. R. & Gibbon, J. D. 2004 A bound on mixing efficiency for the advection–diffusion equation. J. Fluid Mech. 521, 105–114.Google Scholar
Trefethen, L. N. 2001 Spectral Methods in MATLAB. Society for Industrial and Applied Mathematics.Google Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377, 2931–2938.CrossRefGoogle Scholar
Wen, B., Dianati, N., Lunasin, E., Chini, G. P. & Doering, C. R. 2012 New upper bounds and reduced dynamical modelling for Rayleigh–Bénard convection in a fluid saturated porous layer. Commun. Nonlinear Sci. Numer. Simul. 17, 2191–2199.CrossRefGoogle Scholar
Whitehead, J. P. & Doering, C. R. 2011 Ultimate state of two-dimensional Rayleigh–Bénard convection between free-slip fixed-temperature boundaries. Phys. Rev. Lett. 106, 244501.Google Scholar
Whitehead, J. P. & Doering, C. R. 2012 Rigid bounds on heat transport by a fluid between slippery boundaries. J. Fluid Mech. 707, 241–259.Google Scholar