Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T20:11:29.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall temperature and bluntness effects on hypersonic laminar separation at a compression corner

Published online by Cambridge University Press:  02 July 2021

D. Exposito Open the ORCID record for D. Exposito [Opens in a new window] ,
S.L. Gai Open the ORCID record for S.L. Gai [Opens in a new window]  and
A.J. Neely Open the ORCID record for A.J. Neely [Opens in a new window]
D. Exposito*
Affiliation:
School of Engineering and Information Technology, University of New South Wales, Canberra, ACT2612, Australia
S.L. Gai
Affiliation:
School of Engineering and Information Technology, University of New South Wales, Canberra, ACT2612, Australia
A.J. Neely
Affiliation:
School of Engineering and Information Technology, University of New South Wales, Canberra, ACT2612, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

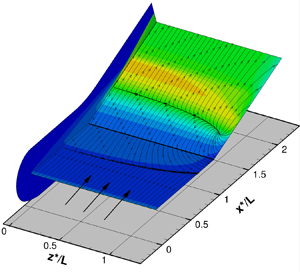
This paper describes a numerical investigation on the effects of wall temperature and leading-edge bluntness on hypersonic laminar separation induced by a finite-span compression corner. The flow conditions were: Mach number 9.66; Reynolds number $1.34 \times 10^6$ per metre; and stagnation temperature 3150 K. The wall to stagnation temperature ratio ($s_w$) varied from 0.095 to 0.333 and was thus in the subcritical range as per the classification of Brown et al. (J. Fluid Mech., vol. 220, 1990, pp. 309–337). Two leading-edge bluntnesses of $40\ \mathrm {\mu }\textrm {m}$ and $200\ \mathrm {\mu }\textrm {m}$ were used in the investigation. Numerical solutions were obtained using a compressible Navier–Stokes solver and compared with triple-deck solutions obtained using the numerical method of Cassel et al. (J. Fluid Mech., vol. 300, 1995, pp. 265–285). Separation was induced by ramp angles of $10^{\circ }$ and $20^{\circ }$, which produced near incipient and large separations. The scaled angles, which increased with wall to stagnation temperature ratio, were not sufficient to induce secondary separation in the main recirculation region. Two regimes of shock interference were identified depending on the wall temperature ratio. The corner instability in the form of a stationary wave-packet identified by Cassel et al. (J. Fluid Mech., vol. 300, 1995, pp. 265–285) for scaled angles $\alpha \geq 3.9$ was investigated but is shown to be a numerical artefact of the algorithm rather than having any physical basis. Increasing both the wall temperature ratio and blunting increased the separation length. And there is an equivalence between cooling the wall and reducing bluntness both leading to a reduced separation length.

JFM classification

Aerodynamics: High-speed flow Boundary Layers: Boundary layer separation Compressible Flows: Hypersonic Flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A1
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Babinsky, H. & Harvey, J.K. 2011 Shock wave-boundary-layer interactions, vol. 32. Cambridge University Press.CrossRefGoogle Scholar
Ball, K.O.W 1967 Wall temperature effect on incipient separation. AIAA J. 5 (12), 2283–2284.CrossRefGoogle Scholar
Bertram, M.H. 1954 Viscous and leading-edge thickness effects on the pressures on the surface of a flat plate in hypersonic flow. J. Aeronaut. Sci. 21 (6), 430–431.CrossRefGoogle Scholar
Bertram, M.H. & Henderson, A. Jr. 1958 Effects of boundary-layer displacement and leading-edge bluntness on pressure distribution, skin friction, and heat transfer of bodies at hypersonic speeds. Tech. Rep. No. NACA-N-4301. NACA.Google Scholar
Bleilebens, M. & Olivier, H. 2006 On the influence of elevated surface temperatures on hypersonic shock wave/boundary layer interaction at a heated ramp model. Shock Waves 15 (5), 301–312.CrossRefGoogle Scholar
Blottner, F.G., Johnson, M. & Ellis, M. 1971 Chemically reacting viscous flow program for multi-component gas mixtures. Tech. Rep. No. SC-RR-70-754. Sandia Labs., Albuquerque, NM.CrossRefGoogle Scholar
Borovoy, V.Y., Mosharov, V.E., Radchenko, V.N., Skuratov, A.S. & Struminskaya, I.V. 2014 Leading edge bluntness effect on the flow in a model air-inlet. Fluid Dyn. 49 (4), 454–467.CrossRefGoogle Scholar
Borovoy, V.Y., Skuratov, A.S. & Struminskaya, I.V. 2008 On the existence of a threshold value of the plate bluntness in the interference of an oblique shock with boundary and entropy layers. Fluid Dyn. 43 (3), 369–379.CrossRefGoogle Scholar
Brauckmann, G.J., Paulson, J.W. Jr. & Weilmuenster, K.J. 1995 Experimental and computational analysis of shuttle orbiter hypersonic trim anomaly. J. Spacecr. Rockets 32 (5), 758–764.CrossRefGoogle Scholar
Brown, S.N., Cheng, H.K. & Lee, C.J. 1990 Inviscid–viscous interaction on triple-deck scales in a hypersonic flow with strong wall cooling. J. Fluid Mech. 220, 309–337.CrossRefGoogle Scholar
Brown, S.N., Khorrami, A.F., Neish, A. & Smith, F.T. 1991 On hypersonic boundary-layer interactions and transition. Phil. Trans. R. Soc. Lond. A 335 (1637), 139–152.Google Scholar
Candler, G.V., Johnson, H.B., Nompelis, I., Gidzak, V.M., Subbareddy, P.K. & Barnhardt, M. 2015 Development of the US3D code for advanced compressible and reacting flow simulations. In 53rd AIAA Aerospace Sciences Meeting, p. 1893. AIAA.CrossRefGoogle Scholar
Candler, G.V., Subbareddy, P.K. & Brock, J.M. 2014 Advances in computational fluid dynamics methods for hypersonic flows. J. Spacecr. Rockets 52 (1), 17–28.CrossRefGoogle Scholar
Cassel, K.W., Ruban, A.I. & Walker, J.D.A. 1995 An instability in supersonic boundary-layer flow over a compression ramp. J. Fluid Mech. 300, 265–285.CrossRefGoogle Scholar
Cassel, K.W., Ruban, A.I. & Walker, J.D.A. 1996 The influence of wall cooling on hypersonic boundary-layer separation and stability. J. Fluid Mech. 321, 189–216.CrossRefGoogle Scholar
Chang, E.W.K., Chan, W.Y.K., McIntyre, T.J. & Veeraragavan, A. 2021 Hypersonic shock impingement on a heated flat plate at mach 7 flight enthalpy. J. Fluid Mech. 908, R1.CrossRefGoogle Scholar
Chapman, D.R., Kuehn, D.M. & Larson, H.K. 1958 Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition. NACA TN REPORT (1356). NACA.Google Scholar
Cheng, H.K. 1993 Perspectives on hypersonic viscous flow research. Annu. Rev. Fluid Mech. 25 (1), 455–484.CrossRefGoogle Scholar
Cheng, H.K., Hall, J.G., Golian, T.C. & Hertzberg, A. 1961 Boundary-layer displacement and leading-edge bluntness effects in high-temperature hypersonic flow. J. Aerosp. Sci. 28 (5), 353–381.CrossRefGoogle Scholar
Chuvakhov, P.V., Borovoy, V.Y., Egorov, I.V., Radchenko, V.N., Olivier, H. & Roghelia, A. 2017 Effect of small bluntness on formation of Görtler vortices in a supersonic compression corner flow. J. Appl. Mechan. Tech. Phys. 58 (6), 975–989.CrossRefGoogle Scholar
Delery, J.M. 1992 Physics of vortical flows. J. Aircr. 29 (5), 856–876.CrossRefGoogle Scholar
Drayna, T., Nompelis, I. & Candler, G. 2006 Numerical simulation of the AEDC waverider at mach 8. In 25th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, p. 2816. AIAA.CrossRefGoogle Scholar
Egorov, I., Neiland, V. & Shredchenko, V. 2011 Three-dimensional flow structures at supersonic flow over the compression ramp. In 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, p. 730. AIAA.CrossRefGoogle Scholar
Fletcher, A.J.P., Ruban, A.I. & Walker, J.D.A. 2004 Instabilities in supersonic compression ramp flow. J. Fluid Mech. 517, 309–330.CrossRefGoogle Scholar
Gadd, G.E. 1957 a An experimental investigation of heat transfer effects on boundary layer separation in supersonic flow. J. Fluid Mech. 2 (2), 105–122.CrossRefGoogle Scholar
Gadd, G.E. 1957 b A review of theoretical work relevant to the problem of heat transfer effects on laminar separation. A.R C Tech. Rep. C.P. (331). Aeronautical Research Council.Google Scholar
Gai, S.L. & Khraibut, A. 2019 Hypersonic compression corner flow with large separated regions. J. Fluid Mech. 877, 471–494.CrossRefGoogle Scholar
Gajjar, J. & Smith, F.T. 1983 On hypersonic self-induced separation, hydraulic jumps and boundary layers with algebraic growth. Mathematika 30 (1), 77–93.CrossRefGoogle Scholar
Grisham, J.R., Dennis, B.H. & Lu, F.K. 2018 Incipient separation in laminar ramp-induced shock-wave/boundary-layer interactions. AIAA J. 56 (2), 524–531.CrossRefGoogle Scholar
Hankey, W.L. 1967 Prediction of incipient separation in shock-boundary-layer interactions. AIAA J. 5 (2), 355–356.CrossRefGoogle Scholar
Holden, M.S. 1967 Theoretical and experimental studies of laminar flow separation on flat plate-wedge compression surfaces in the hypersonic strong interaction regime. Final report. Cornell Aeronautical Lab Inc, Buffalo, NY.Google Scholar
Holden, M.S. 1971 Boundary-layer displacement and leading-edge bluntness effects on attached and separated laminar boundary layers in a compression corner. II-experimental study. AIAA J. 9 (1), 84–93.CrossRefGoogle Scholar
Holden, M.S., Wadhams, T.P., MacLean, M.G. & Dufrene, A.T. 2013 Measurements of real gas effects on regions of laminar shock wave/boundary layer interaction in hypervelocity flows for “blind” code validation studies. In 21st AIAA Computational Fluid Dynamics Conference, p. 2837. AIAA.CrossRefGoogle Scholar
John, B. & Kulkarni, V. 2014 Effect of leading edge bluntness on the interaction of ramp induced shock wave with laminar boundary layer at hypersonic speed. Comput. Fluids 96, 177–190.CrossRefGoogle Scholar
Katzer, E. 1989 On the lengthscales of laminar shock/boundary-layer interaction. J. Fluid Mech. 206, 477–496.CrossRefGoogle Scholar
Kerimbekov, R.M., Ruban, A.I. & Walker, J.D.A. 1994 Hypersonic boundary-layer separation on a cold wall. J. Fluid Mech. 274, 163–195.CrossRefGoogle Scholar
Khraibut, A., Gai, S.L., Brown, L.M. & Neely, A.J. 2017 Laminar hypersonic leading edge separation–a numerical study. J. Fluid Mech. 821, 624–646.CrossRefGoogle Scholar
Khraibut, A., Gai, S.L. & Neely, A.J. 2019 Numerical study of bluntness effects on laminar leading edge separation in hypersonic flow. J. Fluid Mech. 878, 386–419.CrossRefGoogle Scholar
Korolev, G.L., Gajjar, J.S.B. & Ruban, A.I. 2002 Once again on the supersonic flow separation near a corner. J. Fluid Mech. 463, 173–199.CrossRefGoogle Scholar
Lagrée, P.-Y. 1991 Influence de la couche d'entropie sur la longueur de séparation en aérodynamique hypersonique, dans le cadre de la triple couche. C. R. Acad. Sci. Paris II 313, 999–1004.Google Scholar
Legendre, R. 1977 Lignes de courant d'un ecoulement permanent, decollement et separation. 327–335. Rech. Aerospat, France.Google Scholar
Logue, R.P., Gajjar, J.S.B. & Ruban, A.I. 2014 Instability of supersonic compression ramp flow. Phil. Trans. R. Soc. A 372 (2020), 20130342.CrossRefGoogle ScholarPubMed
Mallinson, S.G., Gai, S.L. & Mudford, N.R. 1996 Leading-edge bluntness effects in high enthalpy, hypersonic compression corner flow. AIAA J. 34 (11), 2284–2290.CrossRefGoogle Scholar
Mallinson, S.G., Gai, S.L. & Mudford, N.R. 1997 Establishment of steady separated flow over a compression–corner in a free–piston shock tunnel. Shock Waves 7 (4), 249–253.CrossRefGoogle Scholar
Mallinson, S.G., Mudford, N.R. & Gai, S.L. 2020 Leading-edge bluntness effects in hypervelocity flat plate flow. Phys. Fluids 32 (4), 046106.CrossRefGoogle Scholar
Marini, M. 1998 Effects of flow and geometry parameters on shock-wave boundary-layer interaction phenomena. In 8th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, p. 1570. AIAA.CrossRefGoogle Scholar
Marini, M. 2001 Analysis of hypersonic compression ramp laminar flows under sharp leading edge conditions. Aerosp. Sci. Technol. 5 (4), 257–271. AIAA.CrossRefGoogle Scholar
Mason, W.H. & Lee, J. 1994 Aerodynamically blunt and sharp bodies. J. Spacecr. Rockets 31 (3), 378–382.CrossRefGoogle Scholar
Moeckel, W.E. 1957 Some effects of bluntness on boundary-layer transition and heat transfer at supersonic speeds. NACA Rep. 1312, 1957. Supersedes NACA TN, vol. 3653.Google Scholar
Nagamatsu, H., Sheer, R. Jr. & Wisler, D. 1966 Wall cooling effects on hypersonic boundary layer transition, m (1)= 7.5-15. In 4th Joint Fluid Mechanics, Plasma Dynamics and Lasers Conference, p. 1088. AIAA.Google Scholar
Needham, D.A. 1967 A note on hypersonic incipient separation. AIAA J. 5 (12), 2284–2285.CrossRefGoogle Scholar
Neiland, V.Y. 1969 Theory of laminar boundary layer separation in supersonic flow. Fluid Dyn. 4 (4), 33–35.Google Scholar
Neiland, V.Y. 1970 Asymptotic theory of plane steady supersonic flows with separation zones. Fluid Dyn. 5 (3), 372–381.CrossRefGoogle Scholar
Neiland, V.Y. 1973 Boundary-layer separation on a cooled body and interaction with a hypersonic flow. Fluid Dyn. 8 (6), 931–939.CrossRefGoogle Scholar
Neiland, V.Y., Sokolov, L.A. & Shvedchenko, V.V. 2009 Temperature factor effect on separated flow features in supersonic gas flow. In BAIL 2008-Boundary and Interior Layers, pp. 39–54. Springer.CrossRefGoogle Scholar
Neuenhahn, T. & Olivier, H. 2012 Laminar incipient separation in supersonic and hypersonic flows. Intl J. Aerodyn. 2 (2–4), 114–129.CrossRefGoogle Scholar
Nielsen, J.N., Lynes, L.L. & Goodwin, F.K. 1966 Theory of laminar separated flows on flared surfaces including supersonic flow with heating and cooling. In AGARD Conference Proceedings, vol. 4, p. 37. AGARD Report.Google Scholar
Nompelis, I. & Candler, G.V. 2014 US3D predictions of double-cone and hollow cylinder-flare flows at high-enthalpy. In 44th AIAA Fluid Dynamics Conference, p. 3366. AIAA.CrossRefGoogle Scholar
Park, G., Gai, S.L. & Neely, A.J. 2010 Laminar near wake of a circular cylinder at hypersonic speeds. AIAA J. 48 (1), 236–248.CrossRefGoogle Scholar
Prakash, R., Le Page, L.M., McQuellin, L.P., Gai, S.L. & O'Byrne, S. 2019 Direct simulation Monte Carlo computations and experiments on leading-edge separation in rarefied hypersonic flow. J. Fluid Mech. 879, 633–681.CrossRefGoogle Scholar
Reinartz, B., Ballmann, J., Brown, L., Fischer, C. & Boyce, R. 2007 Shock wave/boundary layer interaction in hypersonic intake flows. In 2nd European Conference on Aero-Space Sciences (EUCASS), Brussels, Belgium, pp. 1–6.Google Scholar
Rizzetta, D.P., Burggraf, O.R. & Jenson, R. 1978 Triple-deck solutions for viscous supersonic and hypersonic flow past corners. J. Fluid Mech. 89 (3), 535–552.CrossRefGoogle Scholar
Ruban, A.I. 1978 Numerical solution of the local asymptotic problem of the unsteady separation of a laminar boundary layer in a supersonic flow. USSR Comput. Maths Math. Phys. 18 (5), 175–187.CrossRefGoogle Scholar
Rudy, D., Thomas, J., Kumar, A., Gnoff, P. & Chakravarthy, S. 1989 A validation study of four Navier–Stokes codes for high-speed flows. In 20th Fluid Dynamics, Plasma Dynamics and Lasers Conference, p. 1838. AIAA.CrossRefGoogle Scholar
Seddougui, S.O., Bowles, R.I. & Smith, F.T. 1991 Surface-cooling effects on compressible boundary-layer instability, and on upstream influence. Eur. J. Mech. B/Fluids 10 (2), 117–145.Google Scholar
Shvedchenko, V.V. 2009 About the secondary separation at supersonic flow over a compression ramp. TsAGI Sci. J. 40 (5), 587–607.CrossRefGoogle Scholar
Smith, F.T. 1988 a Finite-time break-up can occur in any unsteady interacting boundary layer. Mathematika 35 (2), 256–273.CrossRefGoogle Scholar
Smith, F.T. 1988 b A reversed-flow singularity in interacting boundary layers. Proc. R. Soc. Lond. A 420 (1858), 21–52.Google Scholar
Smith, F.T. & Khorrami, A.F. 1994 Hypersonic aerodynamics on thin bodies with interaction and upstream influence. J. Fluid Mech. 277, 85–108.Google Scholar
Smith, F.T. & Khorrami, A.F. 1991 The interactive breakdown in supersonic ramp flow. J. Fluid Mech. 224, 197–215.CrossRefGoogle Scholar
Softley, E. 1969 Boundary layer transition on hypersonic blunt, slender cones. In 2nd Fluid and Plasma Dynamics Conference, p. 705. AIAA.CrossRefGoogle Scholar
Stetson, K. 1979 Effect of bluntness and angle of attack on boundary layer transition on cones and biconic configurations. In 17th Aerospace Sciences Meeting, p. 269. AIAA.CrossRefGoogle Scholar
Stewartson, K. 1970 On laminar boundary layers near corners. Q. J. Mech. Appl. Maths 23 (2), 137–152.CrossRefGoogle Scholar
Stewartson, K. 1975 On the asymptotic theory of separated and unseparated fluid motions. SIAM J. Appl. Maths 28 (2), 501–518.CrossRefGoogle Scholar
Stewartson, K. & Williams, P.G. 1969 Self-induced separation. Proc. R. Soc. Lond. A 312 (1509), 181–206.Google Scholar
Stollery, J.L. 1972 Viscous interaction effects on re-entry aerothermodynamics: theory and experimental results. AGARD Lecture Series, vol. 42. AGARD.Google Scholar
Wagner, A., Schramm, J.M., Hannemann, K., Whitside, R. & Hickey, J.-P. 2017 Hypersonic shock wave boundary layer interaction studies on a flat plate at elevated surface temperature. In International Conference on RailNewcastle Talks, pp. 231–243. Springer.CrossRefGoogle Scholar
Wilke, C.R. 1950 A viscosity equation for gas mixtures. J. Chem. Phys. 18 (4), 517–519.CrossRefGoogle Scholar
Wright, M.J., Candler, G.V. & Bose, D. 1998 Data-parallel line relaxation method for the Navier–Stokes equations. AIAA J. 36 (9), 1603–1609.CrossRefGoogle Scholar