Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T16:44:57.075Z Has data issue: false hasContentIssue false
  • English
  • Français

Vorticity transport in the leading-edge vortex on a rotating blade

Published online by Cambridge University Press:  03 March 2014

Craig J. Wojcik  and
James H. J. Buchholz
Craig J. Wojcik
Affiliation:
Department of Mechanical and Industrial Engineering, University of Iowa, Iowa City, IA 52242, USA IIHR - Hydroscience and Engineering, Iowa City, IA 52242, USA
James H. J. Buchholz*
Affiliation:
Department of Mechanical and Industrial Engineering, University of Iowa, Iowa City, IA 52242, USA IIHR - Hydroscience and Engineering, Iowa City, IA 52242, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Vorticity transport is analysed within the leading-edge vortex generated on a rectangular flat plate of aspect ratio 4 undergoing a starting rotation motion in a quiescent fluid. Two analyses are conducted on the inboard half of the blade to better understand the vorticity transport mechanisms responsible for maintaining the quasi-equilibrium state of the leading-edge vortex. 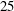An initial global analysis between the $25$ and 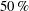$50\, \%$ spanwise positions suggests that, although spanwise velocity is significant, spanwise convection of vorticity is insufficient to balance the flux of vorticity from the leading-edge shear layer. Subsequent detailed analyses of vorticity transport in planar control volumes at the 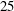$25$ and 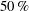$50\, \%$ spanwise positions verify this conclusion and demonstrate that vorticity annihilation due to interaction between the leading-edge vortex and the opposite-sign layer on the plate surface is an important, often dominant, mechanism for regulation of leading-edge-vortex circulation. Thus, it provides an important condition for maintenance of an attached leading-edge vortex on the inboard portion of the blade.

JFM classification

Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 743 , 25 March 2014 , pp. 249 - 261
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansari, S. A., Phillips, N., Stabler, G., Wilkins, P. C., Żbikowski, R. & Knowles, K. 2009 Experimental investigation of some aspects of insect-like flapping flight aerodynamics for application to micro air vehicles. Exp. Fluids 46, 777–798.Google Scholar
Aono, H., Liang, F. & Liu, H. 2007 Near- and far-field aerodynamics in insect hovering flight: an integrated computational study. J. Exp. Biol. 211, 239–257.Google Scholar
Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412, 729–733.Google Scholar
Breton, S.-P., Coton, F. N. & Moe, G. 2008 A study on rotational effects and different stall delay models using a prescribed wake vortex scheme and NREL phase VI experiment data. Wind Energy 11, 459–482.Google Scholar
Carr, Z. R., Chen, C. & Ringuette, M. J. 2012 The effect of aspect ratio on the threedimensional vortex formation of rotating flat-plate wings. In 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Nashville, Tennessee, AIAA Paper 2012-0912.Google Scholar
DeVoria, A., Mahajan, P. & Ringuette, M. J. 2011 Vortex formation and saturation for low-aspect-ratio rotating flat plates at low reynolds number. In 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Orlando, Florida .Google Scholar
Doligalski, T. L., Smith, C. R. & Walker, J. D. A. 1994 Vortex interactions with walls. Annu. Rev. Fluid Mech. 26, 573–616.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013a Investigation of aspect ratio and dynamic effects due to rotation for a revolving wing using high-fidelity simulation. In 51th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Grapevine, Texas .Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013b Three-dimensional flow structure and aerodynamic loading on a revolving wing. Phys. Fluids 25, 034101.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing platforms. J. Fluid Mech. 717, 166–192.Google Scholar
Himmelskamp, H.1945 Profile investigations on a rotating airscrew. PhD thesis, Göttingen.Google Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49, 329–339.CrossRefGoogle Scholar
Kim, D. & Gharib, M. 2011 Flexibility effects on vortex formation of translating plates. J. Fluid Mech. 677, 255–271.Google Scholar
Lentink, D. & Dickinson, M. H. 2009a Biofluiddynamic scaling of flapping, spinning and translating fins and wings. J. Expl Biol. 212, 2691–2704.CrossRefGoogle ScholarPubMed
Lentink, D. & Dickinson, M. H. 2009b Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212, 2705–2719.Google Scholar
Lim, T. T., Teo, C. J., Lua, K. B. & Yeo, K. S. 2009 On the prolong attachment of leading edge vortex on a flapping wing. Mod. Phys. Lett. B 23 (3), 357–360.Google Scholar
Lin, J.-C. & Rockwell, D. 1995 Transient structure of vortex breakdown on a delta wing. AIAA J. 33 (1), 6–12.Google Scholar
Maxworthy, T. 1981 The fluid dynamics of insect flight. Annu. Rev. Fluid Mech. 13, 329–350.Google Scholar
Mayo, D. B. & Jones, A. R. 2013 Evolution and breakdown of a leading edge vortex on a rotating wing. In 51th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Grapevine, Texas, AIAA Paper 2013-0843.Google Scholar
Ol, M. V. & Gharib, M. 2003 Leading-edge vortex structure of nonslender delta wings at low Reynolds number. AIAA J. 41 (2), 16–26.Google Scholar
Ozen, C. A. & Rockwell, D. 2012a Flow structure on a rotating plate. Exp. Fluids 52, 207–223.Google Scholar
Ozen, C. A. & Rockwell, D. 2012b Three-dimensional vortex structure on a rotating wing. J. Fluid Mech. 707, 541–550.Google Scholar
Poelma, C., Dickson, W. B. & Dickinson, M. H. 2006 Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing. Exp. Fluids 41, 213–225.Google Scholar
Shih, C. & Ding, Z. 1996 Unsteady structure of leading-edge vortex flow over a delta wing. In AIAA Paper 96-0664 Reno, Nevada.Google Scholar
Shih, C. & Ding, Z. 2002 Vortex interaction of a delta-wing flowfield. AIAA J. 41 (2), 314–316.CrossRefGoogle Scholar
Tangler, J. L. 2004 Insight into wind turbine stall and post-stall aerodynamics. Wind Energy 7, 247–260.CrossRefGoogle Scholar
Visbal, M. R. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (11), 2685–2697.Google Scholar
Visbal, M. R. & Gordnier, R. E. 1995 Origin of computed unsteadiness in the shear layer of delta wings. J. Aircraft 32 (5), 1146–1148.Google Scholar
Wojcik, C. J. 2012 The dynamics of spanwise vorticity on a rotating flat plate in a starting motion. Master’s thesis, University of Iowa.Google Scholar
Wojcik, C. J. & Buchholz, J. H. J. 2014 Effects of parameter variation on the leading-edge vortex of a rotating flat plate. AIAA J. 52 (2), 348–357.Google Scholar