Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T01:06:40.630Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibration of a two degree-of-freedom flexibly mounted circular cylinder in the crossflow direction

Published online by Cambridge University Press:  28 November 2022

Seyedmohammad Mousavisani ,
Naumi Noshin Chowdhury ,
Hadi Samsam-Khayani Open the ORCID record for Hadi Samsam-Khayani [Opens in a new window] ,
Hamed Samandari Open the ORCID record for Hamed Samandari [Opens in a new window]  and
Banafsheh Seyed-Aghazadeh Open the ORCID record for Banafsheh Seyed-Aghazadeh [Opens in a new window]
Seyedmohammad Mousavisani
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
Naumi Noshin Chowdhury
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
Hadi Samsam-Khayani
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
Hamed Samandari
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
Banafsheh Seyed-Aghazadeh*
Affiliation:
Department of Mechanical Engineering, University of Massachusetts, Dartmouth, MA 02747, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

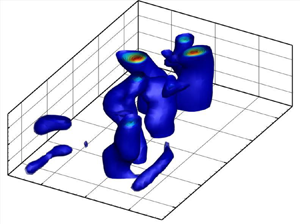
Vortex-induced vibration (VIV) of a two degree-of-freedom (DOF) circular cylinder, placed in the test section of a recirculating water tunnel and free to oscillate in its first two vibrational modes in the crossflow direction, is studied experimentally. The dynamic response of the cylinder is studied for a reduced velocity range of $U^*=4\unicode{x2013}30$ for eigenfrequency ratios in the range of 1.3–3.0. For the two DOF system, while the onset of the VIV response followed a similar lock-in region as those observed for a classical VIV response of a single DOF system, by increasing the reduced velocity a secondary lock-in region was observed over which the oscillations of the cylinder were locked into the system's second mode. In addition, there existed an intermediate range of reduced velocity over which the VIV response consisted of oscillations at a combination of the first two natural modes of the system. As the eigenfrequency ratio between the first two modes increased, the secondary lock-in range was extended to higher reduced velocities and the reduced velocity range over which multi-modal oscillations were observed was decreased. A full map of vortex dynamics in the wake of the cylinder was developed qualitatively and quantitatively using hydrogen bubble flow visualization and time-resolved volumetric particle tracking velocimetry techniques, respectively. A Q-criterion analysis revealed the existence of highly three-dimensional vortex structures in the wake of the cylinder. The spatiotemporal mode analysis using the proper orthogonal decomposition technique revealed strong coupling between the vortex shedding modes in the wake of the cylinder and the structural vibration modes.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex shedding
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 952 , 10 December 2022 , A26
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

These authors contributed equally to this work.

References

REFERENCES

Ardeh, H.A. & Allen, M.S. 2013 Investigating cases of jump phenomenon in a nonlinear oscillatory system. In Topics in Nonlinear Dynamics (ed. G. Kerschen, D. Adams & A. Carrella), vol. 1, pp. 299–318. Springer.CrossRefGoogle Scholar
Bearman, P.W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Bourguet, R., Karniadakis, G.E. & Triantafyllou, M.S. 2011 a Vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 677, 342–382.Google Scholar
Bourguet, R., Karniadakis, G.E. & Triantafyllou, M.S. 2013 Distributed lock-in drives broadband vortex-induced vibrations of a long flexible cylinder in shear flow. J. Fluid Mech. 717, 361–375.CrossRefGoogle Scholar
Bourguet, R., Lucor, D. & Triantafyllou, M.S. 2012 Mono-and multi-frequency vortex-induced vibrations of a long tensioned beam in shear flow. J. Fluids Struct. 32, 52–64.CrossRefGoogle Scholar
Bourguet, R., Modarres-Sadeghi, Y., Karniadakis, G.E. & Triantafyllou, M.S. 2011 b Wake-body resonance of long flexible structures is dominated by counterclockwise orbits. Phys. Rev. Lett. 107 (13), 134502.CrossRefGoogle ScholarPubMed
Carlson, D.W., Currier, T.M. & Modarres-Sadeghi, Y. 2021 Flow-induced vibrations of a square prism free to oscillate in the cross-flow and inline directions. J. Fluid Mech. 919, A2.CrossRefGoogle Scholar
Chaplin, J.R. & Batten, W.M.J. 2014 Simultaneous wake- and vortex-induced vibrations of a cylinder with two degrees of freedom in each direction. Trans. ASME J. Offshore Mech. Arctic Engng 136 (3), 031101.Google Scholar
Chaplin, J.R., Bearman, P.W., Huarte, F.J.H. & Pattenden, R.J. 2005 Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current. J. Fluids Struct. 21 (1), 3–24.CrossRefGoogle Scholar
Chen, L., Wu, J. & Cheng, B. 2019 Volumetric measurement and vorticity dynamics of leading-edge vortex formation on a revolving wing. Exp. Fluids 60 (1), 12.CrossRefGoogle Scholar
Dahl, J.M., Hover, F.S. & Triantafyllou, M.S. 2006 Two-degree-of-freedom vortex-induced vibrations using a force assisted apparatus. J. Fluids Struct. 22 (6–7), 807–818.CrossRefGoogle Scholar
Dahl, J.M., Hover, F.S., Triantafyllou, M.S., Dong, S. & Karniadakis, G.E.M. 2007 Resonant vibrations of bluff bodies cause multivortex shedding and high frequency forces. Phys. Rev. Lett. 99 (14), 144503.CrossRefGoogle ScholarPubMed
Du, L., Jing, X. & Sun, X. 2014 Modes of vortex formation and transition to three-dimensionality in the wake of a freely vibrating cylinder. J. Fluids Struct. 49, 554–573.CrossRefGoogle Scholar
Evangelinos, C., Lucor, D. & Karniadakis, G.E. 2000 DNS-derived force distribution on flexible cylinders subject to vortex-induced vibration. J. Fluids Struct. 14 (3), 429–440.CrossRefGoogle Scholar
Gedikli, E.D., Chelidze, D. & Dahl, J.M. 2018 Observed mode shape effects on the vortex-induced vibration of bending dominated flexible cylinders simply supported at both ends. J. Fluids Struct. 81, 399–417.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C.H.K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Govardhan, R. & Williamson, C.H.K. 2002 Resonance forever: existence of a critical mass and an infinite regime of resonance in vortex-induced vibration. J. Fluid Mech. 473, 147–166.CrossRefGoogle Scholar
Horn, R.A. & Johnson, C.R. 1985 Matrix Analysis. Cambridge University Press.CrossRefGoogle Scholar
Huera-Huarte, F.J. & Bearman, P.W. 2009 Wake structures and vortex-induced vibrations of a long flexible cylinder–Part 1: Dynamic response. J. Fluids Struct. 25 (6), 969–990.CrossRefGoogle Scholar
Hunt, J.C.R., Wray, A.A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Studying turbulence using numerical simulation databases, 2. Proceedings of the 1988 summer program.Google Scholar
Inman, D.J. & Singh, R.C. 1994 Engineering Vibration, vol. 3. Prentice Hall.Google Scholar
Jauvtis, N.A. & Williamson, C.H.K. 2004 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23–62.CrossRefGoogle Scholar
Khalak, A. & Williamson, C.H.K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.CrossRefGoogle Scholar
Konstantinidis, E., Balabani, S. & Yianneskis, M. 2007 Bimodal vortex shedding in a perturbed cylinder wake. Phys. Fluids 19 (1), 011701.CrossRefGoogle Scholar
Lie, H. & Kaasen, K.E. 2006 Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow. J. Fluids Struct. 22 (4), 557–575.CrossRefGoogle Scholar
Lumley, J.L. 2007 Stochastic Tools in Turbulence. Courier Corporation.Google Scholar
Marcollo, H., Eassom, A., Fontaine, E., Tognarelli, M., Beynet, P., Constantinides, Y. & Oakley, O.H. Jr. 2011 Traveling wave response in full-scale drilling riser VIV measurements. In 30th International Conference on Offshore Mechanics and Arctic Engineering, vol. 44397, pp. 523–537.Google Scholar
Nishi, Y. 2013 Power extraction from vortex-induced vibration of dual mass system. J. Sound Vib. 332 (1), 199–212.CrossRefGoogle Scholar
Nishi, Y., Fukuda, K. & Shinohara, W. 2017 Experimental energy harvesting from fluid flow by using two vibrating masses. J. Sound Vib. 394, 321–332.CrossRefGoogle Scholar
Raghavan, K. & Bernitsas, M.M. 2011 Experimental investigation of Reynolds number effect on vortex induced vibration of rigid circular cylinder on elastic supports. Ocean Engng 38 (5), 719–731.CrossRefGoogle Scholar
Saad, Y. 2011 Numerical Methods for Large Eigenvalue Problems. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Sarpkaya, T. 1995 Hydrodynamic damping, flow-induced oscillations, and biharmonic response. Trans. ASME J. Offshore Mech. Arctic Engng 117 (4), 232–238.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Schanz, D., Gesemann, S. & Schröder, A. 2016 Shake-the-box: Lagrangian particle tracking at high particle image densities. Exp. Fluids 57 (5), 70.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Benner, B., Gjokollari, X. & Modarres-Sadeghi, Y. 2021 An experimental investigation of vortex-induced vibration of a curved flexible cylinder. J. Fluid Mech. 927, A21.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Carlson, D.W. & Modarres-Sadeghi, Y. 2015 The influence of taper ratio on vortex-induced vibration of tapered cylinders in the crossflow direction. J. Fluids Struct. 53, 84–95.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Carlson, D.W. & Modarres-Sadeghi, Y. 2017 Vortex-induced vibration and galloping of prisms with triangular cross-sections. J. Fluid Mech. 817, 590–618.CrossRefGoogle Scholar
Seyed-Aghazadeh, B., Edraki, M. & Modarres-Sadeghi, Y. 2019 Effects of boundary conditions on vortex-induced vibration of a fully submerged flexible cylinder. Exp. Fluids 60 (3), 38.CrossRefGoogle Scholar
Seyed-Aghazadeh, B. & Modarres-Sadeghi, Y. 2016 Reconstructing the vortex-induced-vibration response of flexible cylinders using limited localized measurement points. J. Fluids Struct. 65, 433–446.CrossRefGoogle Scholar
Sieber, M., Paschereit, C.O. & Oberleithner, K. 2016 Spectral proper orthogonal decomposition. J. Fluid Mech. 792, 798–828.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures, I. Coherent structures. Q. Appl. Maths, 45 (3), 561–590.CrossRefGoogle Scholar
Taira, K., Brunton, S.L., Dawson, S.T.M., Rowley, C.W., Colonius, T., McKeon, B.J., Schmidt, O.T., Gordeyev, S., Theofilis, V. & Ukeiley, L.S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 4013–4041.CrossRefGoogle Scholar
Trefethen, L.N. & Bau, D. III 1997 Numerical Linear Algebra, vol. 50. SIAM.CrossRefGoogle Scholar
Trim, A.D., Braaten, H., Lie, H. & Tognarelli, M.A. 2005 Experimental investigation of vortex-induced vibration of long marine risers. J. Fluids Struct. 21 (3), 335–361.CrossRefGoogle Scholar
Vandiver, J.K., Marcollo, H., Swithenbank, S. & Jhingran, V. 2005 High mode number vortex-induced vibration field experiments. In Offshore Technology Conference. OnePetro.CrossRefGoogle Scholar
Vicente-Ludlam, D., Barrero-Gil, A. & Velazquez, A. 2015 Enhanced mechanical energy extraction from transverse galloping using a dual mass system. J. Sound Vib. 339, 290–303.CrossRefGoogle Scholar
Wang, Z., Fan, D. & Triantafyllou, M.S. 2021 Illuminating the complex role of the added mass during vortex induced vibration. Phys. Fluids 33 (8), 085120.CrossRefGoogle Scholar
Zanganeh, H. & Srinil, N. 2016 Three-dimensional VIV prediction model for a long flexible cylinder with axial dynamics and mean drag magnifications. J. Fluids Struct. 66, 127–146.CrossRefGoogle Scholar

Mousavisani et al. supplementary movie 1

Movie1: Eigenfrequency ratio=1.7-U*=5.4-Shedding pattern: 2S
Download Mousavisani et al. supplementary movie 1(Video)
Video 11.1 MB

Mousavisani et al. supplementary movie 2

Movie2: Eigenfrequency ratio=1.7-U*=6.7-Shedding pattern: 2S*
Download Mousavisani et al. supplementary movie 2(Video)
Video 11.5 MB

Mousavisani et al. supplementary movie 3

Movie3: Eigenfrequency ratio=1.7-U*=7.9-Shedding pattern: 2P
Download Mousavisani et al. supplementary movie 3(Video)
Video 10.8 MB

Mousavisani et al. supplementary movie 4

Movie4: Eigenfrequency ratio=1.7-U*=9.8-Shedding pattern: SST
Download Mousavisani et al. supplementary movie 4(Video)
Video 11 MB