Published online by Cambridge University Press: 24 March 2017
Flow-induced oscillations of a flexibly mounted triangular prism allowed to oscillate in the cross-flow direction are studied experimentally, covering the entire range of possible angles of attack. For angles of attack smaller than
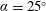 $\unicode[STIX]{x1D6FC}=25^{\circ }$
(where
$\unicode[STIX]{x1D6FC}=25^{\circ }$
(where
 $0^{\circ }$
corresponds to the case where one of the vertices is facing the incoming flow), no oscillation is observed in the entire reduced velocity range tested. At larger angles of attack of
$0^{\circ }$
corresponds to the case where one of the vertices is facing the incoming flow), no oscillation is observed in the entire reduced velocity range tested. At larger angles of attack of
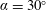 $\unicode[STIX]{x1D6FC}=30^{\circ }$
and
$\unicode[STIX]{x1D6FC}=30^{\circ }$
and
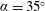 $\unicode[STIX]{x1D6FC}=35^{\circ }$
, there exists a limited range of reduced velocities where the prism experiences vortex-induced vibration (VIV). In this range, the frequency of oscillations locks into the natural frequency twice: once approaching from the Strouhal frequencies and once from half the Strouhal frequencies. Once the lock-in is lost, there is a range with almost-zero-amplitude oscillations, followed by another range of non-zero-amplitude response. The oscillations in this range are triggered when the Strouhal frequency reaches a value three times the natural frequency of the system. Large-amplitude low-frequency galloping-type oscillations are observed in this range. At angles of attack larger than
$\unicode[STIX]{x1D6FC}=35^{\circ }$
, there exists a limited range of reduced velocities where the prism experiences vortex-induced vibration (VIV). In this range, the frequency of oscillations locks into the natural frequency twice: once approaching from the Strouhal frequencies and once from half the Strouhal frequencies. Once the lock-in is lost, there is a range with almost-zero-amplitude oscillations, followed by another range of non-zero-amplitude response. The oscillations in this range are triggered when the Strouhal frequency reaches a value three times the natural frequency of the system. Large-amplitude low-frequency galloping-type oscillations are observed in this range. At angles of attack larger than
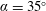 $\unicode[STIX]{x1D6FC}=35^{\circ }$
, once the oscillations start, their amplitude increases continuously with increasing reduced velocity. At these angles of attack, the initial VIV-type response gives way to a galloping-type response at higher reduced velocities. High-frequency vortex shedding is observed in the wake of the prism for the ranges with a galloping-type response, suggesting that the structure’s oscillations are at a lower frequency compared with the shedding frequency and its amplitude is larger than the typical VIV-type amplitudes, when galloping-type response is observed.
$\unicode[STIX]{x1D6FC}=35^{\circ }$
, once the oscillations start, their amplitude increases continuously with increasing reduced velocity. At these angles of attack, the initial VIV-type response gives way to a galloping-type response at higher reduced velocities. High-frequency vortex shedding is observed in the wake of the prism for the ranges with a galloping-type response, suggesting that the structure’s oscillations are at a lower frequency compared with the shedding frequency and its amplitude is larger than the typical VIV-type amplitudes, when galloping-type response is observed.
Present address: Miami University, Middletown, OH 45042, USA.