Published online by Cambridge University Press: 01 December 2016
The effect of viscosity and thermal conduction on the acoustics in a shear layer above an impedance wall is investigated numerically and asymptotically by solving the linearised compressible Navier–Stokes equations (LNSE). It is found that viscothermal effects can be as important as shear, and therefore including shear while neglecting viscothermal effects by solving the linearised Euler equations (LEE) is questionable. In particular, the damping rate of upstream-propagating waves is found to be under-predicted by the LEE, and dramatically so in certain instances. The effects of viscosity on stability are also found to be important. Short wavelength disturbances are stabilised by viscosity, greatly altering the characteristic wavelength and maximum growth rate of instability. For the parameters considered here (chosen to be typical of aeroacoustic situations), the Reynolds number below which the flow stabilises ranges from 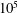 $10^{5}$ to
$10^{5}$ to 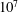 $10^{7}$. By assuming a thin but non-zero-thickness boundary layer, asymptotic analysis leads to a system of boundary layer governing equations for the acoustics. This system may be solved numerically to produce an effective impedance boundary condition, applicable at the wall of a uniform inviscid flow, that accounts for both the shear and viscosity within the boundary layer. An alternative asymptotic analysis in the high-frequency limit yields a different set of boundary layer equations, which are solved to yield analytic solutions. The acoustic mode shapes and axial wavenumbers from both asymptotic analyses compare well with numerical solutions of the full LNSE. A closed-form effective impedance boundary condition is derived from the high-frequency asymptotics, suitable for application in frequency domain numerical simulations. Finally, surface waves are considered, and it is shown that a viscous flow over an impedance lining supports a greater number of surface wave modes than an inviscid flow.
$10^{7}$. By assuming a thin but non-zero-thickness boundary layer, asymptotic analysis leads to a system of boundary layer governing equations for the acoustics. This system may be solved numerically to produce an effective impedance boundary condition, applicable at the wall of a uniform inviscid flow, that accounts for both the shear and viscosity within the boundary layer. An alternative asymptotic analysis in the high-frequency limit yields a different set of boundary layer equations, which are solved to yield analytic solutions. The acoustic mode shapes and axial wavenumbers from both asymptotic analyses compare well with numerical solutions of the full LNSE. A closed-form effective impedance boundary condition is derived from the high-frequency asymptotics, suitable for application in frequency domain numerical simulations. Finally, surface waves are considered, and it is shown that a viscous flow over an impedance lining supports a greater number of surface wave modes than an inviscid flow.
A preliminary version of some of this work was presented at the 21st AIAA/CEAS Aeroacoustics Conference, Dallas, 2015, paper 2015-2229.