Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Koglin, Bernd
1972.
Experimentelle Untersuchungen zur Sedimentation von Teilchenkomplexen in Suspensionen.
Chemie Ingenieur Technik,
Vol. 44,
Issue. 8,
p.
515.
Morrison, Frank A.
1973.
Breakup of a bubble chain.
Chemical Engineering Science,
Vol. 28,
Issue. 4,
p.
1115.
Narayanan, S.
Goossens, L.H.J.
and
Kossen, N.W.F.
1974.
Coalescence of two bubbles rising in line at low reynolds numbers.
Chemical Engineering Science,
Vol. 29,
Issue. 10,
p.
2071.
Crowley, Joseph M.
1976.
Clumping instability of a falling horizontal lattice.
The Physics of Fluids,
Vol. 19,
Issue. 9,
p.
1296.
Crowley, Joseph M.
1977.
Clumping instability which is not predicted by the nearest neighbor approximation.
The Physics of Fluids,
Vol. 20,
Issue. 2,
p.
339.
Caflisch, R.
and
Papanicolaou, G. C.
1983.
Dynamic Theory of Suspensions with Brownian Effects.
SIAM Journal on Applied Mathematics,
Vol. 43,
Issue. 4,
p.
885.
Lévy, T.
and
Sanchez-Palencia, E.
1985.
Einstein-like approximation for homogenization with small concentration. II—Navier-Stoke equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 9,
Issue. 11,
p.
1255.
Singh, P.
Caussignac, Ph.
Fortes, A.
Joseph, D. D.
and
Lundgren, T.
1989.
Stability of periodic arrays of cylinders across the stream by direct simulation.
Journal of Fluid Mechanics,
Vol. 205,
Issue. -1,
p.
553.
Al Taweel, A.M.
Militzer, J.
Kan, J.M.
and
Hamdullahpur, F.
1989.
Motion of hydrodynamic aggregates.
Powder Technology,
Vol. 59,
Issue. 3,
p.
173.
Kamel, M.T.
and
Tory, E.M.
1990.
Sedimentation of clusters of identical spheres II. Periodic motion of three spheres.
Powder Technology,
Vol. 63,
Issue. 2,
p.
187.
Chen, Ye-Mon
Jang, Chien-Sheng
Cai, Ping
and
Fan, Liang-Shih
1991.
On the formation and disintegration of particle clusters in a liquid—solid transport bed.
Chemical Engineering Science,
Vol. 46,
Issue. 9,
p.
2253.
Lahiri, Rangan
and
Ramaswamy, Sriram
1997.
Are Steadily Moving Crystals Unstable?.
Physical Review Letters,
Vol. 79,
Issue. 6,
p.
1150.
Tong, P.
and
Ackerson, B. J.
1998.
Analogies between colloidal sedimentation and turbulent convection at high Prandtl numbers.
Physical Review E,
Vol. 58,
Issue. 6,
p.
R6931.
Smith, Terence N.
1998.
A model of settling velocity.
Chemical Engineering Science,
Vol. 53,
Issue. 2,
p.
315.
Simha, R. Aditi
and
Ramaswamy, Sriram
1999.
Traveling Waves in a Drifting Flux Lattice.
Physical Review Letters,
Vol. 83,
Issue. 16,
p.
3285.
Lahiri, Rangan
Barma, Mustansir
and
Ramaswamy, Sriram
2000.
Strong phase separation in a model of sedimenting lattices.
Physical Review E,
Vol. 61,
Issue. 2,
p.
1648.
Felderhof, B. U.
2003.
Mesoscopic stability and sedimentation waves in settling periodic arrays.
Physical Review E,
Vol. 68,
Issue. 5,
Lee, Jonghoon
and
Ladd, Anthony J. C.
2005.
Axial Segregation of a Settling Suspension in a Rotating Cylinder.
Physical Review Letters,
Vol. 95,
Issue. 4,
Ekiel-Jeżewska, M. L.
and
Felderhof, B. U.
2005.
Periodic sedimentation of three particles in periodic boundary conditions.
Physics of Fluids,
Vol. 17,
Issue. 9,
LEE, JONGHOON
and
LADD, ANTHONY J. C.
2007.
Particle dynamics and pattern formation in a rotating suspension.
Journal of Fluid Mechanics,
Vol. 577,
Issue. ,
p.
183.
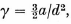 where a is the particle radius and d is the average distance between particles. This result implies that any initial irregularity in a uniform particle distribution will be amplified by viscous forces alone. Significant amplification will occur when the particle has drifted a small multiple of the separation distance, if this separation is not much greater than the particle diameter. Thus, any initially uniform particle layer will form clusters as it drifts through a viscous fluid. The distance in which this clustering occurs will be unaffected by changes in the particle velocity, as long as the Reynolds number remains small. The preferred form of irregularity will consist of small clusters separated by individual particles which trail some distance behind. Experimental verification of these conclusions is presented.
where a is the particle radius and d is the average distance between particles. This result implies that any initial irregularity in a uniform particle distribution will be amplified by viscous forces alone. Significant amplification will occur when the particle has drifted a small multiple of the separation distance, if this separation is not much greater than the particle diameter. Thus, any initially uniform particle layer will form clusters as it drifts through a viscous fluid. The distance in which this clustering occurs will be unaffected by changes in the particle velocity, as long as the Reynolds number remains small. The preferred form of irregularity will consist of small clusters separated by individual particles which trail some distance behind. Experimental verification of these conclusions is presented.