Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T12:48:59.209Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscoelastic liquid curtains: experimental results on the flow of a falling sheet of polymer solution

Published online by Cambridge University Press:  24 June 2019

A. Gaillard Open the ORCID record for A. Gaillard [Opens in a new window] ,
M. Roché Open the ORCID record for M. Roché [Opens in a new window] ,
S. Lerouge ,
C. Gay ,
L. Lebon  and
L. Limat
A. Gaillard*
Affiliation:
Laboratoire Matière et Systemes Complexes, CNRS UMR 7057 Université Denis Diderot, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
M. Roché
Affiliation:
Laboratoire Matière et Systemes Complexes, CNRS UMR 7057 Université Denis Diderot, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
S. Lerouge
Affiliation:
Laboratoire Matière et Systemes Complexes, CNRS UMR 7057 Université Denis Diderot, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
C. Gay
Affiliation:
Laboratoire Matière et Systemes Complexes, CNRS UMR 7057 Université Denis Diderot, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
L. Lebon
Affiliation:
Laboratoire Matière et Systemes Complexes, CNRS UMR 7057 Université Denis Diderot, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
L. Limat
Affiliation:
Laboratoire Matière et Systemes Complexes, CNRS UMR 7057 Université Denis Diderot, 10 rue Alice Domon et Léonie Duquet, 75013 Paris, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We experimentally investigate the extensional flow of a sheet – or curtain – of viscoelastic liquid falling freely from a slot at constant flow rate under gravity. Extruded liquids are aqueous solutions of flexible polyethylene oxide (PEO) and of semi-rigid partially hydrolysed polyacrylamide (HPAM) with low shear viscosities. Velocimetry measurements reveal that the mean velocity field 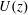$U(z)$ (where $z$ is the distance from the slot exit) does not reduce to a free fall. More precisely, we show that the liquid falls initially with sub-gravitational accelerations up to a distance from the slot which scales as 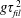$g\unicode[STIX]{x1D70F}_{fil}^{2}$ (where 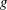$g$ is gravity and 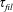$\unicode[STIX]{x1D70F}_{fil}$ is the extensional relaxation time of the liquid) due to the stretching of polymer molecules. Beyond this elastic length, inertia dominates and the local acceleration reaches the asymptotic free-fall value 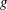$g$. The length of the sub-gravitational part of the curtain is shown to be much larger than the equivalent viscous length 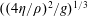$((4\unicode[STIX]{x1D702}/\unicode[STIX]{x1D70C})^{2}/g)^{1/3}$ for Newtonian liquids of density 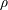$\unicode[STIX]{x1D70C}$ and dynamic viscosity 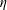$\unicode[STIX]{x1D702}$ which is usually small compared to the curtain length. By analogy with Newtonian curtains, we show that the velocity field 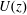$U(z)$ rescales on a master curve. Besides, the flow is shown to be only weakly affected by the history of polymer deformations in the die upstream of the curtain. Furthermore, investigations on the curtain stability reveal that polymer addition reduces the minimum flow rate required to maintain a continuous sheet of liquid.

JFM classification

Non-Newtonian Flows: Polymers Interfacial Flows (free surface): Thin films Non-Newtonian Flows: Viscoelasticity
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 358 - 409
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables, vol. 55. Courier Corporation.Google Scholar
Aidun, C. K. 1987 Mechanics of a free-surface liquid film flow. J. Appl. Mech. 54 (4), 951–954.Google Scholar
Alaie, S. M. & Papanastasiou, T. C. 1991 Film casting of viscoelastic liquid. Polym. Engng Sci. 31 (2), 67–75.Google Scholar
Allain, C., Cloitre, M. & Perrot, P. 1997 Experimental investigation and scaling law analysis of die swell in semi-dilute polymer solutions. J. Non-Newtonian Fluid Mech. 73 (1-2), 51–66.Google Scholar
Amarouchene, Y., Bonn, D., Meunier, J. & Kellay, H. 2001 Inhibition of the finite-time singularity during droplet fission of a polymeric fluid. Phys. Rev. Lett. 86 (16), 3558–3561.Google Scholar
Anna, S. L. & McKinley, G. H. 2001 Elasto-capillary thinning and breakup of model elastic liquids. J. Rheol. 45 (1), 115–138.Google Scholar
Becerra, M. & Carvalho, M. S. 2011 Stability of viscoelastic liquid curtain. Chem. Engng Process. 50 (5), 445–449.Google Scholar
Bird, R. B., Armstrong, R. C., Hassager, O. & Curtiss, C. F. 1987 Dynamics of Polymeric Liquids: Kinetic Theory, vol. 2. Wiley.Google Scholar
Boger, D. V. & Walters, K. 2012 Rheological Phenomena in Focus, vol. 4. Elsevier.Google Scholar
Brandrup, J., Immergut, E. H., Abe, E. A. G. A. & Bloch, D. R. 1989 Polymer Handbook, vol. 7. Wiley.Google Scholar
Brown, D. R. 1961 A study of the behaviour of a thin sheet of moving liquid. J. Fluid Mech. 10 (2), 297–305.Google Scholar
Brunet, P., Flesselles, J.-M. & Limat, L. 2007 Dynamics of a circular array of liquid columns. Eur. Phys. J. B 55 (3), 297–322.Google Scholar
Campo-Deano, L. & Clasen, C. 2010 The slow retraction method (SRM) for the determination of ultra-short relaxation times in capillary breakup extensional rheometry experiments. J. Non-Newtonian Fluid Mech. 165 (23‐24), 1688–1699.Google Scholar
Cartalos, U. & Piau, J. M. 1992 Creeping flow regimes of low concentration polymer solutions in thick solvents through an orifice die. J. Non-Newtonian Fluid Mech. 45 (2), 231–285.Google Scholar
Casanellas, L., Alves, M. A., Poole, R. J., Lerouge, S. & Lindner, A. 2016 The stabilizing effect of shear thinning on the onset of purely elastic instabilities in serpentine microflows. Soft Matt. 12 (29), 6167–6175.Google Scholar
Chen, E. B., Morales, A. J., Chen, C. C., Donatelli, A. A., Bannister, W. W. & Cummings, B. T. 1998 Fluorescein and poly(ethylene oxide) hose stream additives for improved firefighting effectiveness. Fire Technol. 34 (4), 291–306.Google Scholar
Chen, P., Yao, L., Liu, Y., Luo, J., Zhou, G. & Jiang, B. 2012 Experimental and theoretical study of dilute polyacrylamide solutions: effect of salt concentration. J. Mol. Model. 18 (7), 3153–3160.Google Scholar
Chiba, K., Sakatani, T. & Nakamura, K. 1990 Anomalous flow patterns in viscoelastic entry flow through a planar contraction. J. Non-Newtonian Fluid Mech. 36, 193–203.Google Scholar
Chiba, K., Tanaka, S. & Nakamura, K. 1992 The structure of anomalous entry flow patterns through a planar contraction. J. Non-Newtonian Fluid Mech. 42 (3), 315–322.Google Scholar
Clanet, C. & Lasheras, J. C. 1999 Transition from dripping to jetting. J. Fluid Mech. 383, 307–326.Google Scholar
Clarke, N. S. 1966 A differential equation in fluid mechanics. Mathematika 13 (1), 51–53.Google Scholar
Clarke, N. S. 1968 Two-dimensional flow under gravity in a jet of viscous liquid. J. Fluid Mech. 31 (3), 481–500.Google Scholar
Clasen, C., Bico, J., Entov, V. M. & McKinley, G. H. 2009 Gobbling drops: the jetting–dripping transition in flows of polymer solutions. J. Fluid Mech. 636, 5–40.Google Scholar
Clasen, C., Plog, J. P., Kulicke, W.-M., Owens, M., Macosko, C., Scriven, L. E., Verani, M. & McKinley, G. H. 2006 How dilute are dilute solutions in extensional flows? J. Rheol. 50 (6), 849–881.Google Scholar
Crooks, R. & Boger, D. V. 2000 Influence of fluid elasticity on drops impacting on dry surfaces. J. Rheol. 44 (4), 973–996.Google Scholar
Culick, F. E. C. 1960 Comments on a ruptured soap film. J. Appl. Phys. 31 (6), 1128–1129.Google Scholar
Daerr, A. & Mogne, A. 2016 Pendent_drop: an ImageJ plugin to measure the surface tension from an image of a pendent drop. J. Open Res. Softw. 4 (1), e3.Google Scholar
De Gennes, P.-G. 1974 Coil-stretch transition of dilute flexible polymers under ultrahigh velocity gradients. J. Chem. Phys. 60 (12), 5030–5042.Google Scholar
Delvaux, V. & Crochet, M. J. 1990 Numerical simulation of delayed die swell. Rheol. Acta 29 (1), 1–10.Google Scholar
Dombrowski, N. & Johns, W. R. 1963 The aerodynamic instability and disintegration of viscous liquid sheets. Chem. Engng Sci. 18 (3), 203–214.Google Scholar
Dontula, P., Macosko, C. W. & Scriven, L. E. 1998 Model elastic liquids with water-soluble polymers. AIChE J. 44 (6), 1247–1255.Google Scholar
Eggers, J. 2014 Instability of a polymeric thread. Phys. Fluids 26 (3), 033106.Google Scholar
Entov, V. M. & Hinch, E. J. 1997 Effect of a spectrum of relaxation times on the capillary thinning of a filament of elastic liquid. J. Non-Newtonian Fluid Mech. 72 (1), 31–53.Google Scholar
Ewoldt, R. H., Johnston, M. T. & Caretta, L. M. 2015 Experimental challenges of shear rheology: how to avoid bad data. In Complex Fluids in Biological Systems, pp. 207–241. Springer.Google Scholar
Fermigier, M., Limat, L., Wesfreid, J. E., Boudinet, P. & Quilliet, C. 1992 Two-dimensional patterns in Rayleigh–Taylor instability of a thin layer. J. Fluid Mech. 236, 349–383.Google Scholar
Gaillard, A.2018 Flow and stability of a viscoelastic liquid curtain. PhD thesis, Université Sorbonne Paris Cité.Google Scholar
Graessley, W. W. 1980 Polymer chain dimensions and the dependence of viscoelastic properties on concentration, molecular weight and solvent power. Polymer 21 (3), 258–262.Google Scholar
Graham, M. D. 2003 Interfacial hoop stress and instability of viscoelastic free surface flows. Phys. Fluids 15 (6), 1702–1710.Google Scholar
Gugler, G., Beer, R. & Mauron, M. 2010 Coatability of viscoelastic liquid curtain. In Proceedings of the 15th International Coating Science and Technology Symposium, St. Paul, Minnesota.Google Scholar
Herrchen, M. & Öttinger, H. C. 1997 A detailed comparison of various fene dumbbell models. J. Non-Newtonian Fluid Mech. 68 (1), 17–42.Google Scholar
Huang, D. C. & White, J. L. 1979 Extrudate swell from slit and capillary dies: an experimental and theoretical study. Polym. Engng Sci. 19 (9), 609–616.Google Scholar
Karim, A. M., Suszynski, W. J., Francis, L. F. & Carvalho, M. S. 2018a Effect of viscosity on liquid curtain stability. AIChE J. 64 (4), 1448–1457.Google Scholar
Karim, A.M., Suszynski, W.J., Griffith, W.B., Pujari, S., Francis, L.F. & Carvalho, M.S. 2018b Effect of viscoelasticity on stability of liquid curtain. J. Non-Newtonian Fluid Mech. 257, 83–94.Google Scholar
Kawale, D., Marques, E., Zitha, P. L., Kreutzer, M. T., Rossen, W. R. & Boukany, P. E. 2017 Elastic instabilities during the flow of hydrolyzed polyacrylamide solution in porous media: effect of pore-shape and salt. Soft Matt. 13 (4), 765–775.Google Scholar
Kays, W. M., Crawford, M. E. & Weigand, B. 2005 Convective Heat and Mass Transfer, vol. 76. McGraw-Hill.Google Scholar
Keshavarz, B., Sharma, V., Houze, E. C., Koerner, M. R., Moore, J. R., Cotts, P. M., Threlfall-Holmes, P. & McKinley, G. H. 2015 Studying the effects of elongational properties on atomization of weakly viscoelastic solutions using Rayleigh Ohnesorge jetting extensional rheometry (ROJER). J. Non-Newtonian Fluid Mech. 222, 171–189.Google Scholar
Larson, R. G. 1992 Instabilities in viscoelastic flows. Rheol. Acta 31 (3), 213–263.Google Scholar
Larson, R. G. 1999 The Structure and Rheology of Complex Fluids (Topics in Chemical Engineering), vol. 86, p. 108. Oxford University Press.Google Scholar
Macosko, C. W. 1994 Rheology: Principles, Measurements, and Applications. Wiley-VCH.Google Scholar
Mathues, W., McIlroy, C., Harlen, O. G. & Clasen, C. 2015 Capillary breakup of suspensions near pinch-off. Phys. Fluids 27 (9), 093301.Google Scholar
McIlroy, C. & Harlen, O. G. 2014 Modelling capillary break-up of particulate suspensions. Phys. Fluids 26 (3), 033101.Google Scholar
McKinley, G. H. 2005 Visco-elasto-capillary thinning and break-up of complex fluids. Annu. Rheol. Rev. 3, 1–48.Google Scholar
McKinley, G. H., Raiford, W. P., Brown, R. A. & Armstrong, R. C. 1991 Nonlinear dynamics of viscoelastic flow in axisymmetric abrupt contractions. J. Fluid Mech. 223, 411–456.Google Scholar
Miller, E., Clasen, C. & Rothstein, J. P. 2009 The effect of step-stretch parameters on capillary breakup extensional rheology (CaBER) measurements. Rheol. Acta 48 (6), 625–639.Google Scholar
Miyamoto, K. & Katagiri, Y. 1997 Curtain coating. In Liquid Film Coating, pp. 463–494. Springer.Google Scholar
Nigen, S. & Walters, K. 2002 Viscoelastic contraction flows: comparison of axisymmetric and planar configurations. J. Non-Newtonian Fluid Mech. 102 (2), 343–359.Google Scholar
Oliveira, M. S., Yeh, R. & McKinley, G. H. 2006 Iterated stretching, extensional rheology and formation of beads-on-a-string structures in polymer solutions. J. Non-Newtonian Fluid Mech. 137 (1–3), 137–148.Google Scholar
Papanastasiou, T. C., Macosko, C. W., Scriven, L. E. & Chen, Z. 1987 Fiber spinning of viscoelastic liquid. AIChE J. 33 (5), 834–842.Google Scholar
Petrie, C. J. S. 1979 Elongational Flows. Pitman.Google Scholar
Purnode, B. & Crochet, M. J. 1996 Flows of polymer solutions through contractions. Part 1. Flows of polyacrylamide solutions through planar contractions. J. Non-Newtonian Fluid Mech. 65 (2–3), 269–289.Google Scholar
Ramos, J. I. 1996 Planar liquid sheets at low Reynolds numbers. Intl J. Numer. Meth. Fluids 22 (10), 961–978.Google Scholar
Richardson, S. 1970 The die swell phenomenon. Rheol. Acta 9 (2), 193–199.Google Scholar
Roche, J. S., Grand, N. L., Brunet, P., Lebon, L. & Limat, L. 2006 Pertubations on a liquid curtain near break-up: wakes and free edges. Phys. Fluids 18 (8), 082101.Google Scholar
Rodd, L. E., Scott, T. P., Boger, D. V., Cooper-White, J. J. & McKinley, G. H. 2005 The inertio-elastic planar entry flow of low-viscosity elastic fluids in micro-fabricated geometries. J. Non-Newtonian Fluid Mech. 129 (1), 1–22.Google Scholar
Rodd, L. E., Scott, T. P., Cooper-White, J. J., Boger, D. V. & McKinley, G. H. 2007 Role of the elasticity number in the entry flow of dilute polymer solutions in micro-fabricated contraction geometries. J. Non-Newtonian Fluid Mech. 143 (2-3), 170–191.Google Scholar
Rodd, L. E., Scott, T. P., Cooper-White, J. J. & McKinley, G. H. 2005 Capillary break-up rheometry of low-viscosity elastic fluids. Appl. Rheol. 15 (1), 12–27.Google Scholar
Rothstein, J. P. & McKinley, G. H. 1999 Extensional flow of a polystyrene boger fluid through a 4: 1: 4 axisymmetric contraction/expansion. J. Non-Newtonian Fluid Mech. 86 (1), 61–88.Google Scholar
Rubinstein, M. & Colby, R. H. 2003 Polymer physics, vol. 23. Oxford University Press.Google Scholar
Satoh, N., Tomiyama, H. & Kajiwara, T. 2001 Viscoelastic simulation of film casting process for a polymer melt. Polym. Engng Sci. 41 (9), 1564–1579.Google Scholar
Sattler, R., Gier, S., Eggers, J. & Wagner, C. 2012 The final stages of capillary break-up of polymer solutions. Phys. Fluids 24 (2), 023101.Google Scholar
Sattler, R., Wagner, C. & Eggers, J. 2008 Blistering pattern and formation of nanofibers in capillary thinning of polymer solutions. Phys. Rev. Lett. 100 (16), 164502.Google Scholar
Savva, N. & Bush, J. W. M. 2009 Viscous sheet retraction. J. Fluid Mech. 626, 211–240.Google Scholar
Sevilla, A. 2011 The effect of viscous relaxation on the spatiotemporal stability of capillary jets. J. Fluid Mech. 684, 204–226.Google Scholar
Stelter, M., Brenn, G., Yarin, A. L., Singh, R. P. & Durst, F. 2002 Investigation of the elongational behavior of polymer solutions by means of an elongational rheometer. J. Rheol. 46 (2), 507–527.Google Scholar
Sünderhauf, G., Raszillier, H. & Durst, F. 2002 The retraction of the edge of a planar liquid sheet. Phys. Fluids 14 (1), 198–208.Google Scholar
Tanner, R. I. 1970 A theory of die-swell. J. Polym. Sci. B 8 (12), 2067–2078.Google Scholar
Tanner, R. I. 2000 Engineering Rheology, vol. 52. Oxford University Press.Google Scholar
Tanner, R. I. 2005 A theory of die-swell revisited. J. Non-Newtonian Fluid Mech. 129 (2), 85–87.Google Scholar
Taylor, G. 1959 The dynamics of thin sheets of fluid. III. Disintegration of fluid sheets. Proc. R. Soc. Lond. A 313–321.Google Scholar
Tirtaatmadja, V., McKinley, G. H. & Cooper-White, J. J. 2006 Drop formation and breakup of low viscosity elastic fluids: effects of molecular weight and concentration. Phys. Fluids 18 (4), 043101.Google Scholar
Villermaux, E. & Clanet, C. 2002 Life of a flapping liquid sheet. J. Fluid Mech. 462, 341–363.Google Scholar
Virk, P. S. 1975 Drag reduction fundamentals. AIChE J. 21 (4), 625–656.Google Scholar
White, J. L. & Roman, J. F. 1976 Extrudate swell during the melt spinning of fibersinfluence of rheological properties and take-up force. J. Appl. Polym. Sci. 20 (4), 1005–1023.Google Scholar
Wu, X. Y., Hunkeler, D., Hamielec, A. E., Pelton, R. H. & Woods, D. R. 1991 Molecular weight characterization of poly(acrylamide-co-sodium acrylate). I. Viscometry. J. Appl. Polym. Sci. 42 (7), 2081–2093.Google Scholar
Zell, A., Gier, S., Rafai, S. & Wagner, C. 2010 Is there a relation between the relaxation time measured in caber experiments and the first normal stress coefficient? J. Non-Newtonian Fluid Mech. 165 (19), 1265–1274.Google Scholar
Zhang, G., Zhou, J. S., Zhai, Y. A., Liu, F. Q. & Gao, G. 2008 Effect of salt solutions on chain structure of partially hydrolyzed polyacrylamide. J. Central South University of Technology 15 (1), 80–83.Google Scholar