Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T09:37:15.028Z Has data issue: false hasContentIssue false
  • English
  • Français

Vesicle dynamics in large amplitude oscillatory extensional flow

Published online by Cambridge University Press:  02 November 2021

Charlie Lin Open the ORCID record for Charlie Lin [Opens in a new window] ,
Dinesh Kumar Open the ORCID record for Dinesh Kumar [Opens in a new window] ,
Channing M. Richter Open the ORCID record for Channing M. Richter [Opens in a new window] ,
Shiyan Wang Open the ORCID record for Shiyan Wang [Opens in a new window] ,
Charles M. Schroeder Open the ORCID record for Charles M. Schroeder [Opens in a new window]  and
Vivek Narsimhan Open the ORCID record for Vivek Narsimhan [Opens in a new window]
Charlie Lin
Affiliation:
Davidson School of Chemical Engineering, Purdue University, West Lafayette, IN 47907, USA
Dinesh Kumar
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Channing M. Richter
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Shiyan Wang
Affiliation:
Davidson School of Chemical Engineering, Purdue University, West Lafayette, IN 47907, USA
Charles M. Schroeder*
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA Department of Materials Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Vivek Narsimhan*
Affiliation:
Davidson School of Chemical Engineering, Purdue University, West Lafayette, IN 47907, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

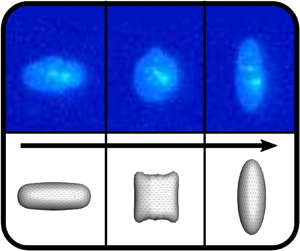
Although the behaviour of fluid-filled vesicles in steady flows has been extensively studied, far less is understood regarding the shape dynamics of vesicles in time-dependent oscillatory flows. Here, we investigate the nonlinear dynamics of vesicles in large amplitude oscillatory extensional (LAOE) flows using both experiments and boundary integral (BI) simulations. Our results characterize the transient membrane deformations, dynamical regimes and stress response of vesicles in LAOE in terms of reduced volume (vesicle asphericity), capillary number (${Ca}$, dimensionless flow strength) and Deborah number (${De}$, dimensionless flow frequency). Results from single vesicle experiments are found to be in good agreement with BI simulations across a wide range of parameters. Our results reveal three distinct dynamical regimes based on vesicle deformation: pulsating, reorienting and symmetrical regimes. We construct phase diagrams characterizing the transition of vesicle shapes between pulsating, reorienting and symmetrical regimes within the two-dimensional Pipkin space defined by ${De}$ and ${Ca}$. Contrary to observations on clean Newtonian droplets, vesicles do not reach a maximum length twice per strain rate cycle in the reorienting and pulsating regimes. The distinct dynamics observed in each regime result from a competition between the flow frequency, flow time scale and membrane deformation time scale. By calculating the particle stresslet, we quantify the nonlinear relationship between average vesicle stress and strain rate. Additionally, we present results on tubular vesicles that undergo shape transformation over several strain cycles. Broadly, our work provides new information regarding the transient dynamics of vesicles in time-dependent flows that directly informs bulk suspension rheology.

JFM classification

Biological Fluid Dynamics: Capsule/cell dynamics Low-Reynolds-number flows: Boundary integral methods Micro-/Nano-fluid dynamics: Microfluidics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 929 , 25 December 2021 , A43
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abreu, D., Levant, M., Steinberg, V. & Seifert, U. 2014 Fluid vesicles in flow. Adv. Colloid Interface Sci. 208, 129–141.CrossRefGoogle ScholarPubMed
Abreu, D. & Seifert, U. 2013 Noisy nonlinear dynamics of vesicles in flow. Phys. Rev. Lett. 110 (23), 238103.CrossRefGoogle ScholarPubMed
Angelova, M.I., Soléau, S., Méléard, P., Faucon, F. & Bothorel, P. 1992 Preparation of giant vesicles by external ac electric fields. kinetics and applications. In Trends in Colloid and Interface Science VI (ed. C. Helm, M. Lösche & H. Möhwald), pp. 127–131. Steinkopff.CrossRefGoogle Scholar
Avital, Y.Y. & Farago, O. 2015 Small membranes under negative surface tension. J. Chem. Phys. 142 (12), 03B619_1.CrossRefGoogle ScholarPubMed
Bagatolli, L. & Sunil Kumar, P.B. 2009 Phase behavior of multicomponent membranes: experimental and computational techniques. Soft Matt. 5, 3234–3248.CrossRefGoogle Scholar
Boal, D. 2002 Mechanics of the Cell Cambridge. Cambridge University Press.Google Scholar
Bryngelson, S.H. & Freund, J.B. 2019 Non-modal Floquet stability of capsules in large-amplitude oscillatory extensional flow. Eur. J. Mech. B/Fluids 77, 171–176.CrossRefGoogle Scholar
Callens, N., Minetti, C., Coupier, G., Mader, M.-A., Dubois, F., Misbah, C. & Podgorski, T. 2008 Hydrodynamic lift of vesicles under shear flow in microgravity. Europhys. Lett. 83 (2), 24002.CrossRefGoogle Scholar
Cirak, F., Ortiz, M. & Schröder, P. 2000 Subdivision surfaces: a new paradigm for thin-shell finite-element analysis. Intl J. Numer. Meth. Engng 47 (12), 2039–2072.3.0.CO;2-1>CrossRefGoogle Scholar
Dahl, J.B., Narsimhan, V., Gouveia, B., Kumar, S., Shaqfeh, E.S.G. & Muller, S.J. 2016 Experimental observation of the asymmetric instability of intermediate-reduced-volume vesicles in extensional flow. Soft Matt. 12 (16), 3787–3796.CrossRefGoogle ScholarPubMed
Danker, G., Biben, T., Podgorski, T., Verdier, C. & Misbah, C. 2007 Dynamics and rheology of a dilute suspension of vesicles: higher-order theory. Phys. Rev. E 76 (4), 041905.CrossRefGoogle ScholarPubMed
Danker, G., Verdier, C. & Misbah, C. 2008 Rheology and dynamics of vesicle suspension in comparison with droplet emulsion. J. Non-Newtonian Fluid Mech. 152 (1), 156–167. 4th International workshop on Nonequilibrium Theromdynamics and Complex Fluids.CrossRefGoogle Scholar
Deschamps, J., Kantsler, V., Segre, E. & Steinberg, V. 2009 Dynamics of a vesicle in general flow. Proc. Natl Acad. Sci. 106 (28), 11444–11447.CrossRefGoogle ScholarPubMed
Deuling, H.J. & Helfrich, W. 1976 The curvature elasticity of fluid membranes: a catalogue of vesicle shapes. J. Phys. 37 (11), 1335–1345.CrossRefGoogle Scholar
Dimova, R. & Marques, C. 2019 The Giant Vesicle Book. CRC Press.CrossRefGoogle Scholar
Dobereiner, H.-G., Selchow, O. & Lipowsky, R. 1999 Spontaneous curvature of fluid vesicles induced by trans-bilayer sugar asymmetry. Eur. Biophys. J. 28 (2), 174–178.Google Scholar
Domachuk, P., Tsioris, K., Omenetto, F.G. & Kaplan, D.L. 2010 Bio-microfluidics: biomaterials and biomimetic designs. Adv. Mater. 22 (2), 249–260.CrossRefGoogle ScholarPubMed
Duffy, M.G. 1982 Quadrature over a pyramid or cube of integrands with a singularity at a vertex. SIAM J. Numer. Anal. 19 (6), 1260–1262.CrossRefGoogle Scholar
Farutin, A., Biben, T. & Misbah, C. 2010 Analytical progress in the theory of vesicles under linear flow. Phys. Rev. E 81, 061904.CrossRefGoogle ScholarPubMed
Farutin, A. & Misbah, C. 2012 a Rheology of vesicle suspensions under combined steady and oscillating shear flows. J. Fluid Mech. 700, 362–381.CrossRefGoogle Scholar
Farutin, A. & Misbah, C. 2012 b Squaring, parity breaking, and s tumbling of vesicles under shear flow. Phys. Rev. Lett. 109 (24), 248106.CrossRefGoogle ScholarPubMed
Helfrich, W. 1973 Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C 28, 693–703.CrossRefGoogle ScholarPubMed
Henriksen, J. & Ipsen, J. 2004 Measurement of membrane elasticity by micro-pipette aspiration. Eur. Phys. J. E 14 (2), 149–167.CrossRefGoogle ScholarPubMed
Huang, S.-L. & MacDonald, R.C. 2004 Acoustically active liposomes for drug encapsulation and ultrasound-triggered release. Biochim. Biophys. Acta Biomembr. 1665 (1–2), 134–141.CrossRefGoogle ScholarPubMed
Hyun, K., Wilhelm, M., Klein, C.O., Cho, K.S., Nam, J.G., Ahn, K.H., Lee, S.J., Ewoldt, R.H. & McKinley, G.H. 2011 A review of nonlinear oscillatory shear tests: analysis and application of large amplitude oscillatory shear (laos). Prog. Polym. Sci. 36 (12), 1697–1753.CrossRefGoogle Scholar
Kantsler, V., Segre, E. & Steinberg, V. 2007 Vesicle dynamics in time-dependent elongation flow: wrinkling instability. Phys. Rev. Lett. 99 (17), 178102.CrossRefGoogle ScholarPubMed
Kantsler, V., Segre, E. & Steinberg, V. 2008 Dynamics of interacting vesicles and rheology of vesicle suspension in shear flow. Europhys. Lett. 82 (5), 58005.CrossRefGoogle Scholar
Kantsler, V. & Steinberg, V. 2005 Orientation and dynamics of a vesicle in tank-treading motion in shear flow. Phys. Rev. Lett. 95, 258101.CrossRefGoogle ScholarPubMed
Kantsler, V. & Steinberg, V. 2006 Transition to tumbling and two regimes of tumbling motion of a vesicle in shear flow. Phys. Rev. Lett. 96, 036001.CrossRefGoogle ScholarPubMed
Kodama, A., Morandi, M., Ebihara, R., Jimbo, T., Toyoda, M., Sakuma, Y., Imai, M., Puff, N. & Angelova, M.I. 2018 Migration of deformable vesicles induced by ionic stimuli. Langmuir 34 (38), 11484–11494.CrossRefGoogle ScholarPubMed
Kumar, D., Richter, C.M. & Schroeder, C.M. 2020 a Conformational dynamics and phase behavior of lipid vesicles in a precisely controlled extensional flow. Soft Matt. 16 (2), 337–347.CrossRefGoogle Scholar
Kumar, D., Richter, C.M. & Schroeder, C.M. 2020 b Double-mode relaxation of highly deformed anisotropic vesicles. Phys. Rev. E 102 (1), 010605.CrossRefGoogle ScholarPubMed
Kumar, D., Shenoy, A., Deutsch, J. & Schroeder, C.M. 2020 c Automation and flow control for particle manipulation. Curr. Opin. Chem. Engng 29, 1–8.CrossRefGoogle Scholar
Kumar, D., Shenoy, A., Li, S. & Schroeder, C.M. 2019 Orientation control and nonlinear trajectory tracking of colloidal particles using microfluidics. Phys. Rev. Fluids 4 (11), 114203.CrossRefGoogle Scholar
Leal, L.G. 1992 Laminar Flow and Convective Transport Processes: Scaling Principles and Asymptotic Analysis. Butterworth-Heinemann.Google Scholar
Lebedev, V.V., Turitsyn, K.S. & Vergeles, S.S. 2007 Dynamics of nearly spherical vesicles in an external flow. Phys. Rev. Lett. 99 (21), 218101.CrossRefGoogle Scholar
Levant, M., Deschamps, J., Afik, E. & Steinberg, V. 2012 Characteristic spatial scale of vesicle pair interactions in a plane linear flow. Phys. Rev. E 85, 056306.CrossRefGoogle Scholar
Li, X. & Sarkar, K. 2005 a Drop dynamics in an oscillating extensional flow at finite Reynolds numbers. Phys. Fluids 17 (2), 027103.CrossRefGoogle Scholar
Li, X. & Sarkar, K. 2005 b Numerical investigation of the rheology of a dilute emulsion of drops in an oscillating extensional flow. J. Non-Newtonian Fluid Mech. 128 (2–3), 71–82.CrossRefGoogle Scholar
Lim, D., Kamotani, Y., Cho, B., Mazumder, J. & Takayama, S. 2003 Fabrication of microfluidic mixers and artificial vasculatures using a high-brightness diode-pumped nd:yag laser direct write method. Lab Chip 3, 318–323.CrossRefGoogle ScholarPubMed
Lin, C. & Narsimhan, V. 2019 Shape stability of deflated vesicles in general linear flows. Phys. Rev. Fluids 4 (12), 123606.CrossRefGoogle Scholar
Mader, M., Vitkova, V., Abkarian, M., Viallat, A. & Podgorski, T. 2006 Dynamics of viscous vesicles in shear flow. Eur. Phys. J. E 19 (4), 389–397.CrossRefGoogle ScholarPubMed
Misbah, C. 2006 Vacillating breathing and tumbling of vesicles under shear flow. Phys. Rev. Lett. 96 (2), 028104.CrossRefGoogle ScholarPubMed
Narsimhan, V., Spann, A.P. & Shaqfeh, E.S.G. 2014 The mechanism of shape instability for a vesicle in extensional flow. J. Fluid Mech. 750, 144–190.CrossRefGoogle Scholar
Narsimhan, V., Spann, A.P. & Shaqfeh, E.S.G. 2015 Pearling, wrinkling, and buckling of vesicles in elongational flows. J. Fluid Mech. 777, 1–26.CrossRefGoogle Scholar
Noguchi, H. & Gompper, G. 2005 Dynamics of fluid vesicles in shear flow: effect of membrane viscosity and thermal fluctuations. Phys. Rev. E 72 (1), 011901.CrossRefGoogle ScholarPubMed
Podgorski, T., Callens, N., Minetti, C., Coupier, G., Dubois, F. & Misbah, C. 2011 Dynamics of vesicle suspensions in shear flow between walls. Microgravity Sci. Technol. 23 (2), 263–270.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Rawicz, W., Olbrich, K.C., McIntosh, T., Needham, D. & Evans, E. 2000 Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79 (1), 328–339.CrossRefGoogle ScholarPubMed
Sakashita, A., Urakami, N., Ziherl, P. & Imai, M. 2012 Three-dimensional analysis of lipid vesicle transformations. Soft Matt. 8 (33), 8569–8581.CrossRefGoogle Scholar
Seifert, U. 1997 Configurations of fluid membranes and vesicles. Adv. Phys. 46 (1), 13–137.CrossRefGoogle Scholar
Shenoy, A., Kumar, D., Hilgenfeldt, S. & Schroeder, C.M. 2019 Flow topology during multiplexed particle manipulation using a stokes trap. Phys. Rev. Appl. 12 (5), 054010.CrossRefGoogle Scholar
Shenoy, A., Rao, C.V. & Schroeder, C.M. 2016 Stokes trap for multiplexed particle manipulation and assembly using fluidics. Proc. Natl. Acad. Sci. 113 (15), 3976–3981.CrossRefGoogle ScholarPubMed
Shenoy, A., Tanyeri, M. & Schroeder, C.M. 2015 Characterizing the performance of the hydrodynamic trap using a control-based approach. Microfluid Nanofluidics 18 (5–6), 1055–1066.CrossRefGoogle Scholar
Spann, A.P., Zhao, H. & Shaqfeh, E.S.G. 2014 Loop subdivision surface boundary integral method simulations of vesicles at low reduced volume ratio in shear and extensional flow. Phys. Fluids 26 (3), 031902.CrossRefGoogle Scholar
Turitsyn, K.S. & Vergeles, S.S. 2008 Wrinkling of vesicles during transient dynamics in elongational flow. Phys. Rev. Lett. 100 (2), 028103.CrossRefGoogle ScholarPubMed
Vitkova, V., Mader, M.-A., Polack, B., Misbah, C. & Podgorski, T. 2008 Micro-macro link in rheology of erythrocyte and vesicle suspensions. Biophys. J. 95 (6), L33–L35.CrossRefGoogle ScholarPubMed
Vlahovska, P.M. & Gracia, R.S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75, 016313.CrossRefGoogle ScholarPubMed
Vlahovska, P.M., Podgorski, T. & Misbah, C. 2009 Vesicles and red blood cells in flow: from individual dynamics to rheology. C. R. Phys. 10 (8), 775–789.CrossRefGoogle Scholar
Wilhelm, M. 2002 Fourier-transform rheology. Macromol. Mater. Engng 287 (2), 83–105.3.0.CO;2-B>CrossRefGoogle Scholar
Yu, M., Lira, R.B., Riske, K.A., Dimova, R. & Lin, H. 2015 Ellipsoidal relaxation of deformed vesicles. Phys. Rev. Lett. 115 (12), 128303.CrossRefGoogle ScholarPubMed
Zabusky, N.J., Segre, E., Deschamps, J., Kantsler, V. & Steinberg, V. 2011 Dynamics of vesicles in shear and rotational flows: modal dynamics and phase diagram. Phys. Fluids 23 (4), 041905.CrossRefGoogle Scholar
Zhao, H. & Shaqfeh, E.S.G. 2013 The dynamics of a non-dilute vesicle suspension in a simple shear flow. J. Fluid Mech. 725, 709–731.CrossRefGoogle Scholar
Zhao, H., Spann, A.P. & Shaqfeh, E.S.G. 2011 The dynamics of a vesicle in a wall-bound shear flow. Phys. Fluids 23 (12), 121901.CrossRefGoogle Scholar
Zhou, H., Gabilondo, B.B., Losert, W. & van de Water, W. 2011 Stretching and relaxation of vesicles. Phys. Rev. E 83 (1), 011905.CrossRefGoogle ScholarPubMed
Zhou, Y. & Schroeder, C.M. 2016 a Single polymer dynamics under large amplitude oscillatory extension. Phys. Rev. Fluids 1 (5), 053301.CrossRefGoogle Scholar
Zhou, Y. & Schroeder, C.M. 2016 b Transient and average unsteady dynamics of single polymers in large-amplitude oscillatory extension. Macromolecules 49 (20), 8018–8030.CrossRefGoogle Scholar
Ziherl, P. & Svetina, S. 2005 Nonaxisymmetric phospholipid vesicles: rackets, boomerangs, and starfish. Europhys. Lett. 70 (5), 690.CrossRefGoogle Scholar

Lin et al. supplementary movie 1

See pdf file for movie caption

Download Lin et al. supplementary movie 1(Video)
Video 2.1 MB

Lin et al. supplementary movie 2

See pdf file for movie caption

Download Lin et al. supplementary movie 2(Video)
Video 4.5 MB

Lin et al. supplementary movie 3

See pdf file for movie caption

Download Lin et al. supplementary movie 3(Video)
Video 2.9 MB

Lin et al. supplementary movie 4

See pdf file for movie caption

Download Lin et al. supplementary movie 4(Video)
Video 6.3 MB

Lin et al. supplementary movie 5

See pdf file for movie caption

Download Lin et al. supplementary movie 5(Video)
Video 5.9 MB

Lin et al. supplementary movie 6

See pdf file for movie caption

Download Lin et al. supplementary movie 6(Video)
Video 5.9 MB

Lin et al. supplementary movie 7

See pdf file for movie caption

Download Lin et al. supplementary movie 7(Video)
Video 7.1 MB

Lin et al. supplementary movie 8

See pdf file for movie captions

Download Lin et al. supplementary movie 8(Video)
Video 373.9 KB

Lin et al. supplementary movie 9

See pdf file for movie caption

Download Lin et al. supplementary movie 9(Video)
Video 351.4 KB

Lin et al. supplementary movie 10

See pdf file for movie caption

Download Lin et al. supplementary movie 10(Video)
Video 342.6 KB
Supplementary material: PDF

Lin et al. supplementary material

Captions for movies 1-10

Download Lin et al. supplementary material(PDF)
PDF 17.2 KB
Supplementary material: PDF

Lin et al. supplementary material

Supplementary data and figures

Download Lin et al. supplementary material(PDF)
PDF 990.3 KB