Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Davidson, B. J.
and
Riley, N.
1972.
Jets induced by oscillatory motion.
Journal of Fluid Mechanics,
Vol. 53,
Issue. 2,
p.
287.
Clark, C.
1972.
Blood Flow from the Heart.
Engineering in Medicine,
Vol. 1,
Issue. 3,
p.
57.
Zalosh, R. G.
and
Nelson, W. G.
1973.
Pulsating flow in a curved tube.
Journal of Fluid Mechanics,
Vol. 59,
Issue. 4,
p.
693.
Hall, P.
1974.
Unsteady viscous flow in a pipe of slowly varying cross-section.
Journal of Fluid Mechanics,
Vol. 64,
Issue. 2,
p.
209.
Chandran, K. B.
Swanson, W. M.
Ghista, D. N.
and
Vayo, H. W.
1974.
Oscillatory flow in thin-walled curved elastic tubes.
Annals of Biomedical Engineering,
Vol. 2,
Issue. 4,
p.
392.
Smith, F. T.
1975.
Pulsatile flow in curved pipes.
Journal of Fluid Mechanics,
Vol. 71,
Issue. 1,
p.
15.
Yao, L.-S.
and
Berger, S. A.
1975.
Entry flow in a curved pipe.
Journal of Fluid Mechanics,
Vol. 67,
Issue. 1,
p.
177.
Riley, N.
1975.
The steady streaming induced by a vibrating cylinder.
Journal of Fluid Mechanics,
Vol. 68,
Issue. 4,
p.
801.
Riley, N.
1975.
Unsteady Laminar Boundary Layers.
SIAM Review,
Vol. 17,
Issue. 2,
p.
274.
1976.
Centrifugal instability of a Stokes layer: linear theory.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 350,
Issue. 1662,
p.
299.
Dore, B. D.
1976.
Double boundary layers in standing surface waves.
pure and applied geophysics,
Vol. 114,
Issue. 4,
p.
629.
1976.
Fluid flow into a curved pipe.
Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences,
Vol. 351,
Issue. 1664,
p.
71.
Murata, S.
Miyake, Y.
and
Inaba, T.
1976.
Laminar flow in a curved pipe with varying curvature.
Journal of Fluid Mechanics,
Vol. 73,
Issue. 4,
p.
735.
Chandran, K.B.
Yearwood, T.L.
and
Wieting, D.W.
1979.
An experimental study of pulsatile flow in a curved tube.
Journal of Biomechanics,
Vol. 12,
Issue. 10,
p.
793.
Duck, P. W.
and
Smith, F. T.
1979.
Steady streaming induced between oscillating cylinders.
Journal of Fluid Mechanics,
Vol. 91,
Issue. 01,
p.
93.
Rabadi, N. J.
Simon, H. A.
and
Chow, J. C. F.
1980.
NUMERICAL SOLUTION FOR FULLY DEVELOPED, LAMINAR PULSATING FLOW IN CURVED TUBES.
Numerical Heat Transfer,
Vol. 3,
Issue. 2,
p.
225.
Christov, Chr.
and
Zapryanov, Z.
1980.
Oscillatory fully developed viscous flow in a toroidal tube.
Computer Methods in Applied Mechanics and Engineering,
Vol. 22,
Issue. 1,
p.
49.
Duck, P. W.
1980.
Linear centrifugal instability of a thick Stokes’ layer.
The Physics of Fluids,
Vol. 23,
Issue. 11,
p.
2178.
Lin, J. Y.
and
Tarbell, J. M.
1980.
An experimental and numerical study of periodic flow in a curved tube.
Journal of Fluid Mechanics,
Vol. 100,
Issue. 03,
p.
623.
Lin, J. Y.
and
Tarbell, J. M.
1980.
Periodic flow in a curved tube.
AIChE Journal,
Vol. 26,
Issue. 1,
p.
165.
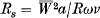 , where
, where 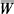 is a typical velocity along the axis of the pipe, and asymptotic theories are developed for both small and large values of this parameter. For sufficiently small values of it is found that the secondary flow in the interior of the pipe is in the opposite sense to that predicted for a steady pressure gradient, and this is verified qualitatively by an experiment described at the end of the paper.
is a typical velocity along the axis of the pipe, and asymptotic theories are developed for both small and large values of this parameter. For sufficiently small values of it is found that the secondary flow in the interior of the pipe is in the opposite sense to that predicted for a steady pressure gradient, and this is verified qualitatively by an experiment described at the end of the paper.