Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-26T07:34:36.813Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsteady force generation and vortex dynamics of pitching and plunging aerofoils

Published online by Cambridge University Press:  06 August 2012

Yeon Sik Baik ,
Luis P. Bernal ,
Kenneth Granlund  and
Michael V. Ol
Yeon Sik Baik*
Affiliation:
Department of Aerospace Engineering, University of Michigan, Ann Arbor, MI 48105, USA
Luis P. Bernal
Affiliation:
Department of Aerospace Engineering, University of Michigan, Ann Arbor, MI 48105, USA
Kenneth Granlund
Affiliation:
Air Force Research Laboratory, Wright-Patterson Air Force Base, Dayton, OH 45433, USA
Michael V. Ol
Affiliation:
Air Force Research Laboratory, Wright-Patterson Air Force Base, Dayton, OH 45433, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Experimental studies of the flow topology, leading-edge vortex dynamics and unsteady force produced by pitching and plunging flat-plate aerofoils in forward flight at Reynolds numbers in the range 5000–20 000 are described. We consider the effects of varying frequency and plunge amplitude for the same effective angle-of-attack time history. 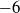The effective angle-of-attack history is a sinusoidal oscillation in the range to 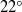with mean of and amplitude of 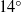. The reduced frequency is varied in the range 0.314–1.0 and the Strouhal number range is 0.10–0.48. Results show that for constant effective angle of attack, the flow evolution is independent of Strouhal number, and as the reduced frequency is increased the leading-edge vortex (LEV) separates later in phase during the downstroke. The LEV trajectory, circulation and area are reported. It is shown that the effective angle of attack and reduced frequency determine the flow evolution, and the Strouhal number is the main parameter determining the aerodynamic force acting on the aerofoil. At low Strouhal numbers, the lift coefficient is proportional to the effective angle of attack, indicating the validity of the quasi-steady approximation. Large values of force coefficients (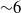) are measured at high Strouhal number. The measurement results are compared with linear potential flow theory and found to be in reasonable agreement. During the downstroke, when the LEV is present, better agreement is found when the wake effect is ignored for both the lift and drag coefficients.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Biological Fluid Dynamics: Swimming/flying Vortex Flows: Vortex dynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 709 , 25 October 2012 , pp. 37 - 68
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Anderson, J. M., Streitlein, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.CrossRefGoogle Scholar
2. Baik, Y. 2011 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils at low Reynolds number. PhD thesis, University of Michigan.CrossRefGoogle Scholar
3. Baik, Y., Rausch, J. M., Bernal, L. P., Shyy, W. & Ol, M. 2010 Experimental study of governing parameters in pitching and plunging aerofoil at low Reynolds number. AIAA Paper 2010-0388.CrossRefGoogle Scholar
4. Birch, J. M., Dickson, W. B. & Dickinson, M. H. 2004 Force production and flow structure of the leading edge vortex on flapping wings. J. Expl Biol. 207, 1063–1072.CrossRefGoogle Scholar
5. Bisplinghoff, R. L., Ashley, H. & Halfman, R. L. 1996 Aeroelasticity. Dover.Google Scholar
6. Chakraborty, P., Balachandar, S. & Adrian, R. J. 2005 On the relationship between local vortex identification schemes. J. Fluid Mech. 535, 189–214.CrossRefGoogle Scholar
7. Dabiri, J. O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.Google Scholar
8. Dickinson, M. H. & Gotz, K. G. 1993 Unsteady aerodynamic performance on model wings at low Reynolds numbers. J. Expl Biol. 174, 45–64.CrossRefGoogle Scholar
9. von Ellenrieder, K. D. & Posthos, S. 2008 PIV measurements of the asymmetric wake of a two-dimensional heaving hydrofoil. Exp. Fluids 44, 733–745.CrossRefGoogle Scholar
10. Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384, 626–630.CrossRefGoogle Scholar
11. Garrick, I. E. 1936 Propulsion of a flapping and oscillating aerofoil. NASA Tech. Rep. 567.Google Scholar
12. Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
13. Godoy-Diana, R., Aider, J. L. & Wesfried, J. E. 2009 A model for the symmetry breaking of the reverse Bénard–von Kármán vortex street produced by a flapping foil. J. Fluid Mech. 622, 23–32.CrossRefGoogle Scholar
14. Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Tech. 12, 1422–1429.CrossRefGoogle Scholar
15. Granlund, K., Ol, M. & Bernal, L. 2011 Experiments on pitching plates: force and flow field measurements at low Reynolds numbers. AIAA Paper 2011-0872.Google Scholar
16. Hover, F. S., Haugsdal, O. & Triantafyllou, M. S. 2004 Forces on oscillating foils for propulsion and maneuvering. J. Fluid Struct. 19, 37–47.CrossRefGoogle Scholar
17. Jones, A. R. & Babinsky, H. 2010 Unsteady lift generation on rotating wings at low Reynolds numbers. J. Aircraft 47, 1013–1021.Google Scholar
18. Kang, C.-K., Baik, Y., Bernal, L. P., Ol, M. V. & Shyy, W. 2009 Fluid dynamics of pitching and plunging aerofoils of Reynolds number between and . AIAA Paper 2009-536.CrossRefGoogle Scholar
19. von Kármán, T. & Sears, W. R. 1938 Airfoil theory for non-uniform motion. J. Aeronaut. Sci. 5, 379–390.CrossRefGoogle Scholar
20. Koochesfahani, M. M. 1989 Vortical patterns in the wake of an oscillating aerofoil. AIAA J. 27, 1200–1205.CrossRefGoogle Scholar
21. Krueger, P., Dabiri, J. O. & Gharib, M. 2006 The formation number of vortex rings formed in uniform background co-flow. J. Fluid Mech. 556, 147–166.CrossRefGoogle Scholar
22. Lai, J. C. S. & Platzer, M. 1999 Jet characteristics of a plunging aerofoil. AIAA J. 37, 1529–1537.Google Scholar
23. Lighthill, M. J. 1969 Hydromechanics of aquatic animal propulsion. Annu. Rev. Fluid Mech. 1, 413–446.CrossRefGoogle Scholar
24. Lua, K. B., Lim, T. T., Yeo, K. S. & Oo, G. Y. 2007 Wake-structure formation of a heaving two-dimensional elliptic aerofoil. AIAA J. 45, 1571–1583.CrossRefGoogle Scholar
25. Maxworthy, T. 1981 The fluid dynamics of insect flight. Annu. Rev. Fluid Mech. 13, 329–350.CrossRefGoogle Scholar
26. McCroskey, W. J. 1981 The phenomenon of dynamic stall. Tech. Rep. 81264. NASA Tech. Mem.Google Scholar
27. McCroskey, W. J. 1982 Unsteady aerofoils. Annu. Rev. Fluid Mech 14, 285–311.Google Scholar
28. McGowan, G. Z., Granlund, K., Ol, M. V., Gopalarathnam, A. & Edwards, J. R. 2011 Investigations of lift-based pitch–plunge equivalence for aerofoils at low Reynolds numbers. AIAA J. 49, 1511–1524.CrossRefGoogle Scholar
29. Milano, M. & Gharib, M. 2005 Uncovering the physics of flapping flat plates with artificial evolution. J. Fluid Mech. 534, 403–409.CrossRefGoogle Scholar
30. Ohmi, K., Coutanceau, M., Daube, O. & Loc, T. P. 1991 Further experiments on vortex formation around an oscillating and translating aerofoil at large incidences. J. Fluid Mech. 225, 607–630.CrossRefGoogle Scholar
31. Ohmi, K., Coutanceau, M., Loc, T. P. & Dulieu, A. 1990 Vortex formation around an oscillating and translating aerofoil at large incidences. J. Fluid Mech. 211, 37–60.Google Scholar
32. Ol, M., Bernal, L. P., Kang, C. & Shyy, W. 2009 Shallow and deep dynamic stall for flapping low Reynolds number aerofoils. Exp. Fluids 46, 883–901.CrossRefGoogle Scholar
33. Ol, M., McAuliffe, B. R., Hanff, E. S., Scholz, U. & Kaehler, Ch. 2005 Comparison of laminar separation bubble measurements on a low Reynolds number aerofoil in three facilities. AIAA Paper 2005-5149.Google Scholar
34. Platzer, M., Jones, K., Young, J. & Lai, J. 2008 Flapping wing aerodynamics: progress and challenges. AIAA J. 46, 2136–2149.CrossRefGoogle Scholar
35. Polhamus, E. C. 1966 A concept of the vortex lift of sharp-edge delta wings based on a leading-edge-suction analogy. Tech. Rep. NASA Technical Note.Google Scholar
36. Read, D. A., Hover, F. S. & Triantafyllou, M. S. 2003 Effect of angle of attack profiles in flapping foil propulsion. J. Fluid Struct. 17, 163–183.Google Scholar
37. Ringuette, M., Michelle, M. & Gharib, M. 2007 Role of the tip vortex in the force generation of low-aspect-ratio normal flat plates. J. Fluid Mech. 581, 453–468.CrossRefGoogle Scholar
38. Rival, D., Prangemeier, T. & Tropea, C. 2009 The influence of aerofoil kinematics on the formation of leading-edge vortices in bio-inspired flight. Exp. Fluids 46, 823–833.Google Scholar
39. Rival, D. & Tropea, C. 2010 Characteristics of pitching and plunging aerofoils under dynamic-stall conditions. J. Aircraft 47, 80–86.Google Scholar
40. Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206, 4195–4208.CrossRefGoogle ScholarPubMed
41. Shyy, W., Lian, Y., Viieru, D. & Liu, H. 2008 Aerodynamics of Low Reynolds Number Flyers. Cambridge University Press.Google Scholar
42. Shyy, W. & Liu, H. 2007 Flapping wings and aerodynamics lift: the role of leading-edge vortices. AIAA J. 45, 2817–2819.Google Scholar
43. Strickland, J. H. & Graham, G. M. 1987 Force coefficients for a NACA-0015 aerofoil undergoing constant pitch rate motions. AIAA J. 25, 622–624.Google Scholar
44. Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2004 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. J. Fluid Struct. 19, 37–47.Google Scholar
45. Theodorsen, T. 1935 General theory of aerodynamic instability and the mechanism of flutter. NACA Tech. Rep. 496.Google Scholar
46. Triantafyllou, G. S., Triantafyllou, M. S. & Grosenbaugh, M. A. 1992 Optimal thrust development in oscillating foils with applications to fish propulsion. J. Fluid Struct. 7, 205–224.CrossRefGoogle Scholar
47. Visbal, M. R. & Shang, J. S. 1989 Investigation of the flow structure around a rapidly pitching aerofoil. AIAA J. 27, 1044–1051.CrossRefGoogle Scholar
48. Young, J. & Lai, J. C. S. 2004 Oscillation frequency and amplitude effects on the wake of a punging aerofoil. AIAA J. 42, 2042–2052.CrossRefGoogle Scholar