Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-05T02:58:09.972Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniform-momentum zones in a turbulent pipe flow

Published online by Cambridge University Press:  10 December 2019

Xue Chen ,
Yongmann M. Chung Open the ORCID record for Yongmann M. Chung [Opens in a new window]  and
Minping Wan Open the ORCID record for Minping Wan [Opens in a new window]
Xue Chen
Affiliation:
School of Engineering and Centre for Scientific Computing, University of Warwick, CoventryCV4 7AL, UK Department of Mechanics and Aerospace Engineering and Guangdong Provincial Key Laboratory of Fundamental Turbulence Research and Applications, Southern University of Science and Technology, 518055, China
Yongmann M. Chung*
Affiliation:
School of Engineering and Centre for Scientific Computing, University of Warwick, CoventryCV4 7AL, UK
Minping Wan
Affiliation:
Department of Mechanics and Aerospace Engineering and Guangdong Provincial Key Laboratory of Fundamental Turbulence Research and Applications, Southern University of Science and Technology, 518055, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The characteristics and dynamics of the uniform-momentum zones (UMZ) and UMZ interfaces in a fully developed turbulent pipe flow are studied using direct numerical simulation at $Re_{\unicode[STIX]{x1D70F}}=500$. The multiple UMZs detected from the probability density functions of the instantaneous streamwise velocity following de Silva et al. (J. Fluid Mech., vol. 786, 2016, pp. 309–331) showed similarities to both turbulent channel and boundary layer flows (TBL): the hierarchical structural distribution of thinner UMZs with thinner interfaces nearer the wall, accompanied with sharper and larger jumps in the streamwise velocity at the UMZ interface. The conditional average results indicate that channel and pipe are very similar quantitatively whereas pipe and TBL display significant discrepancies. The innermost UMZs in pipe flow exhibit different behaviours to the other UMZs in pipes. The contortion of the UMZ interface representing the meandering of coherent motions with high- and low-momentum streaks is examined three-dimensionally. The meandering of UMZ in both two and three dimensions intensifies away from the wall and is always wavier in the azimuthal direction than the streamwise direction. The UMZs in the near-wall region capture the small-scale velocity fluctuation of the near-wall cycle and show asymmetric modulation of $Q2$ ejections over $Q4$ sweeps. The asymmetric modulation of ejections over sweeps decreases from the wall towards the pipe centre and the opposite trend of elevated $Q4$ sweeps is observed for the innermost UMZs. Near the wall, the ejection regions are very spiky compared to the flat sweep regions whereas, in the pipe centre, the large-scale ejections are relatively flat and the sweep regions are spikier.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 884 , 10 February 2020 , A25
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R., Meinhart, C. & Tompkins, C. D. 2000 Vortex organisation in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Agostini, L. & Leschziner, M. A. 2014 On the influence of outer large-scale structures on near-wall turbulence in channel flow. Phys. Fluids 26, 075107.Google Scholar
Agostini, L. & Leschziner, M. A. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28, 015107.CrossRefGoogle Scholar
Antonia, R. A., Teitel, M., Kim, J. & Browne, L. W. B. 1992 Low-Reynolds-number effects in a fully developed turbulent channel flow. J. Fluid Mech. 236, 579–605.CrossRefGoogle Scholar
Baars, W. J., Hutchins, N. & Marusic, I. 2017 Reynolds number trend of hierarchies and scale interactions in turbulent boundary layers. Phil. Trans. R. Soc. Lond. A 375, 20160077.Google ScholarPubMed
Bautista, J. C. C., Ebadi, A., White, C. M., Chini, G. P. & Klewicki, J. C. 2019 A uniform momentum zone-vortical fissure model of the turbulent boundary layer. J. Fluid Mech. 858, 609–633.CrossRefGoogle Scholar
Chin, C., Ooi, A. S. H., Marusic, I. & Blackburn, H. M. 2010 The influence of pipe length on turbulence statistics computed from direct numerical simulation data. Phys. Fluids 22 (11), 115107.CrossRefGoogle Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.CrossRefGoogle Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91 (3), 475–495.CrossRefGoogle Scholar
Fan, D., Xu, J., Yao, M. X. & Hickey, J.-P. 2019 On the detection of internal interfacial layers in turbulent flows. J. Fluid Mech. 872, 198–217.CrossRefGoogle Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 nek5000 Web page. http://nek5000.mcs.anl.gov.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Illingworth, S. J., Monty, J. P. & Marusic, I. 2018 Estimating large-scale structures in wall turbulence using linear models. J. Fluid Mech. 842, 146–162.CrossRefGoogle Scholar
Jiménez, J., del Álamo, J. C. & Flores, O. 2004 The large-scale dynamics of near-wall turbulence. J. Fluid Mech. 505, 179–199.CrossRefGoogle Scholar
Jung, S. Y. & Chung, Y. M. 2012 Large-eddy simulations of accelerated turbulent flow in a circular pipe. Intl J. Heat Fluid Flow 33 (1), 1–8.CrossRefGoogle Scholar
Kevin, M. J. & Hutchins, N. 2019 The meandering behaviour of large-scale structures in turbulent boundary layers. J. Fluid Mech. 865, R1.CrossRefGoogle Scholar
Kwon, Y.2016 The quiescent core of turbulent channel and pipe flows. PhD thesis, University of Melbourne.Google Scholar
Kwon, Y. S., Philip, J., de Silva, C. M., Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.CrossRefGoogle Scholar
Laskari, A., de Kat, R., Hearst, R. J. & Ganapathisubramani, B. 2018 Time evolution of uniform momentum zones in a turbulent boundary layer. J. Fluid Mech. 842, 554–590.CrossRefGoogle Scholar
Marusic, I. 2001 On the role of large-scale structures in wall turbulence. Phys. Fluids 13 (3), 735–743.CrossRefGoogle Scholar
Marusic, I. & Hutchins, N. 2008 Study of the log-layer structure in wall turbulence over a very large range of Reynolds number. Flow Turbul. Combust. 81, 115–130.CrossRefGoogle Scholar
Marusic, I. & Monty, J. P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layer. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Monty, J. P., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes, and channel flows. Phys. Fluids 21 (11), 111703.CrossRefGoogle Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.CrossRefGoogle Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 694 (7), 694–696.CrossRefGoogle Scholar
Metzger, M. M. & Klewicki, J. C. 2001 A comparative study of near-wall turbulence in high and low Reynolds number boundary layers. Phys. Fluids 13 (3), 692701.CrossRefGoogle Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.CrossRefGoogle Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.CrossRefGoogle Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Rao, K. N., Narasimha, R. & Narayanan, M. A. B. 1971 The bursting phenomenon in a turbulent boundary layer. J. Fluid Mech. 48 (part 2), 339–352.CrossRefGoogle Scholar
Saxton-Fox, T. & McKeon, B. J. 2017 Coherent structures, uniform momentum zones and the streamwise energy spectrum in wall-bounded turbulent flows. J. Fluid Mech. 826, R6.CrossRefGoogle Scholar
de Silva, C. M., Hutchins, N. & Marusic, I. 2016 Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.CrossRefGoogle Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layer. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Wagner, C., Huttl, T. J. & Friedrich, R. 2001 Low-Reynolds-number effects derived from direct numerical simulations of turbulent pipe flow. Comput. Fluids 30 (5), 581–590.CrossRefGoogle Scholar
Wang, Z., Orlu, R., Schlatter, P. & Chung, Y. M. 2018 Direct numerical simulation of a turbulent 90 degrees bend pipe flow. Intl J. Heat Fluid Flow 73, 199–208.CrossRefGoogle Scholar
Yang, J., Hwang, J. & Sung, H. J. 2016 Structural organization of the quiescent core region in a turbulent channel flow. Intl J. Heat Fluid Flow 27, 055103.Google Scholar
Yang, J., Hwang, J. & Sung, H. J. 2017 Influence of low- and high-speed structures on the quiescent core region in a turbulent pipe flow. In Proceedings of the Tenth International Symposium on Turbulent and Shear Flow Phenomena.Google Scholar
Yang, M., Meng, H. & Sheng, J. 2001 Dynamics of hairpin vortices generated by a mixing tab in a channel flow. Exp. Fluids 30, 705–722.CrossRefGoogle Scholar

Chen et al. supplementary movie 1

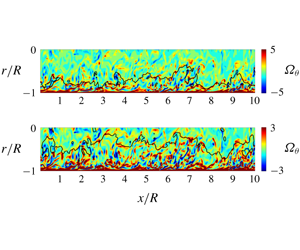
Time evolution of the attachment between UMZ interface defined at 0.9UCL (black line) and azimuthal vortices (coloured contour) in a fixed frame on a streamwise midplane of the pipe.

Download Chen et al. supplementary movie 1(Video)
Video 2.4 MB

Chen et al. supplementary movie 2

Time evolution of the attachment between UMZ interface defined at 0.9UCL (black line) and azimuthal vortices (coloured contour) in a moving frame on a streamwise midplane of the pipe. The frame moves downstream at the bulk mean velocity.

Download Chen et al. supplementary movie 2(Video)
Video 762.9 KB

Chen et al. supplementary movie 3

Time evolution of the attachment between UMZ interface defined at 0.9UCL (black line) and azimuthal vortices (coloured contour) in a fixed frame on a cross-stream plane of the pipe.

Download Chen et al. supplementary movie 3(Video)
Video 2.8 MB

Chen et al. supplementary movie 4

Time evolution of the attachment between UMZ interface defined at 0.9UCL (black line) and azimuthal vortices (coloured contour) in a moving frame on a cross-stream plane of the pipe. The frame moves downstream at the bulk mean velocity.

Download Chen et al. supplementary movie 4(Video)
Video 3.2 MB