Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T14:36:01.776Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-layer hydraulics at the river–ocean interface

Published online by Cambridge University Press:  09 October 2018

Anthony R. Poggioli Open the ORCID record for Anthony R. Poggioli [Opens in a new window]  and
Alexander R. Horner-Devine
Anthony R. Poggioli
Affiliation:
Department of Civil and Environmental Engineering, University of Washington, Seattle, WA 98195, USA
Alexander R. Horner-Devine
Affiliation:
Department of Civil and Environmental Engineering, University of Washington, Seattle, WA 98195, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Liftoff is the hydraulically forced detachment of buoyant freshwater from the channel bottom or seabed that occurs as river water discharges into the coastal ocean. It is a key feature of strongly stratified systems, occurring well upstream in the channel or seaward of the river mouth under sufficiently strong forcing. We present a two-layer hydraulic solution for the river–ocean interface that considers the river, estuary and near-field river plume as a single interlinked system, extending previous work that considered them separately. This unified approach provides a prediction of the liftoff location and free-surface profile for a wide range of forcing conditions, which are characterized in terms of the freshwater Froude number 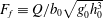$F_{f}\equiv Q/b_{0}\sqrt{g_{0}^{\prime }h_{0}^{3}}$. Here, 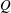$Q$ is the river discharge, 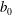$b_{0}$ is the channel width, 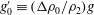$g_{0}^{\prime }\equiv (\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}_{0}/\unicode[STIX]{x1D70C}_{2})g$ is the reduced gravitational acceleration, 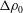$\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}_{0}$ is the density contrast between fresh and ocean water and 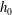$h_{0}$ is the total water depth at the river mouth. The solution is validated with laboratory experiments using an experimental apparatus consisting of a long, sloping river channel that discharges into a deep, wide saltwater basin. The experiments simulate the full range of hydraulic behaviours predicted by the model, from saltwater intrusion to offshore liftoff. For 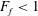$F_{f}<1$, liftoff occurs in the estuary channel and our results show that the relationship between intrusion length and 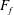$F_{f}$ depends on the channel slope. For 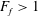$F_{f}>1$, corresponding to flood conditions in many natural systems, liftoff is forced outside the river mouth and the hydraulic coupling between the channel and shelf becomes more important. For these conditions and for intermediate to steeply sloped shelves, the offshore liftoff distance varies linearly with 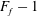$F_{f}-1$, a particularly simple scaling given the nonlinearity and relative complexity of the governing equations. The model and experimental results support a conceptual description of the river–ocean interface that relates the liftoff location, free-surface elevation and the spreading rate of the buoyant river plume.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Geophysical and Geological Flows: River dynamics Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 633 - 672
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present Address: Laboratoire de Physique Statistique, Ecole Normale Supérieure, Paris 75005, France. Email address for correspondence: [email protected]

References

Armi, L. 1986 The hydraulics of two flowing layers with different densities. J. Fluid Mech. 163, 27–58.Google Scholar
Armi, L. & Farmer, D. M. 1986 Maximal two-layer exchange through a contraction with barotropic net flow. J. Fluid Mech. 164, 27–51.Google Scholar
Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31 (2), 209–248.Google Scholar
Bondar, C. 1970 Considerations théoriques sur la dispersion d’un courant liquide de densité réduite et á niveau libre, dans un bassin contenant un liquide d’une plus grande densité. In Symposium on the Hydrology of Deltas, vol. 11, pp. 246–256. UNESCO.Google Scholar
Cenedese, C. & Dalziel, S. 1998 Concentration and depth field determined by the light transmitted through a dyed solution. In Proceedings of Eighth International Symposium on Flow Visualization, pp. 61.1–61.5.Google Scholar
Chatanantavet, P., Lamb, M. P. & Nittrouer, J. A. 2012 Backwater controls of avulsion location on deltas. Geophys. Res. Lett. 39, L01402.Google Scholar
Chen, F., MacDonald, D. G. & Hetland, R. D. 2009 Lateral spreading of a near-field river plume: observations and numerical simulations. J. Geophys. Res. 114, C07013.Google Scholar
Chow, V. T. 1959 Open-Channel Hydraulics. McGraw-Hill.Google Scholar
Christodoulou, G. C. 1986 Interfacial mixing in stratified flows. J. Hydraul. Res. 24, 77–92.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.Google Scholar
Farmer, D. M. & Armi, L. 1986 Maximal two-layer exchange over a sill and through the combination of a sill and contraction with barotropic flow. J. Fluid Mech. 164, 53–76.Google Scholar
Fugate, D. C. & Chant, R. J. 2005 Near-bottom shear stress in a small, highly stratified estuary. J. Geophys. Res. 110, C03022.Google Scholar
Garvine, R. W. 1974 Physical features of the Connecticut River outflow during high discharge. J. Geophys. Res. 79, 831–846.Google Scholar
Garvine, R. W. 1984 Radial spreading of buoyant, surface plumes in coastal waters. J. Geophys. Res. 89, 1989–1996.Google Scholar
Geyer, W. R. 1993 The importance of suppression of turbulence by stratification on the estuarine turbidity maximum. Estuaries 16, 113–125.Google Scholar
Geyer, W. R. & Farmer, D. M. 1989 Tide-induced variation of the dynamics of a salt wedge estuary. J. Phys. Oceanogr. 19, 1060–1072.Google Scholar
Geyer, W. R., Hill, P. S. & Kineke, G. C. 2004 The transport, transformation and dispersal of sediment by buoyant coastal flows. Cont. Shelf Res. 24, 927–949.Google Scholar
Geyer, W. R. & MacCready, P. 2014 The estuarine circulation. Annu. Rev. Fluid Mech. 46, 175–197.Google Scholar
Geyer, W. R. & Ralston, D. K. 2011 The dynamics of strongly stratified estuaries. In Water and Fine Sediment Circulation, 1st edn. (ed. Wolanski, E. & McLusky, D.), Treatise on Estuarine and Coastal Science, vol. 2, pp. 37–51. Elsevier.Google Scholar
Geyer, W. R., Ralston, D. K. & Holleman, R. C. 2017 Hydraulics and mixing in a laterally divergent channel of a highly stratified estuary. J. Geophys. Res. 122, 4743–4760.Google Scholar
Hetland, R. D. 2010 The effects of mixing and spreading on density in near-field river plumes. Dyn. Atmos. Ocean 49, 37–53.Google Scholar
Hetland, R. D. & MacDonald, D. G. 2008 Spreading in the near-field Merrimack River plume. Ocean Model. 21, 12–21.Google Scholar
Hogg, A. McC. & Ivey, G. N. 2003 The Kelvin–Helmholtz to Holmboe instability transition in stratified exchange flows. J. Fluid. Mech. 477, 339–362.Google Scholar
Honegger, D. A., Haller, M. C., Geyer, W. R. & Farquharson, G. 2017 Oblique internal hydraulic jumps at a stratified estuary mouth. J. Phys. Oceanogr. 47, 85–100.Google Scholar
Horner-Devine, A. R, Hetland, R. D. & MacDonald, D. G. 2015 Mixing and transport in coastal river plumes. Annu. Rev. Fluid Mech. 47, 569–594.Google Scholar
Hughes, F. W. & Rattray, M. 1980 Salt flux and mixing in the Columbia River estuary. Estuar. Coast. Mar. Sci. 10 (5), 479–493.Google Scholar
Jay, D. A., Zaron, E. D. & Pan, J. 2010 Initial expansion of the Columbia River tidal plume: theory and remote sensing observations. J. Geophys. Res. 115, C00B15.Google Scholar
Jerolmack, D. J. 2009 Conceptual framework for assessing the response of delta channel networks to holocene sea level rise. Quat. Sci. Rev. 28, 1786–1800.Google Scholar
Karelse, M., Vreugendhil, C. B., Delvinge, G. A. L. & Breusers, H. N. C.1974 Momentum and mass transfer in stratified flows. Tech. Report R880.Google Scholar
Keulegan, G. H.1957 Form characteristics of arrested saline wedge. NBS Report 5482.Google Scholar
Keulegan, G. H. 1966 The mechanism of an arrested saline wedge. In Estuary and Coastline Hydrodynamics (ed. Ippen, A. T.), pp. 546–574. McGraw-Hill.Google Scholar
Kilcher, L. F. & Nash, J. D. 2010 Structure and dynamics of the Columbia River tidal plume front. J. Geophys. Res. 115, C05590.Google Scholar
Kostaschuk, R. A., Church, M. A. & Luternauer, J. L. 1992 Sediment transport over salt-wedge intrusions: fraser river estuary, Canada. Sedimentology 39, 305–317.Google Scholar
Lamb, M. P., Nittrouer, J. A., Mohrig, David & Shaw, John 2012 Backwater and river plume controls on scour upstream of river mouths: implications for fluvio-deltaic morphodynamics. J. Geophys. Res. 117, F01002.Google Scholar
Lane, E. W. 1957 A Study of the Shape of Channels Formed by Natural Streams Flowing in Erodible Material. U.S. Army Corps of Eng., Mo. River Div., Omaha, Nebr.Google Scholar
Lawrence, G. A. 1990 On the hydraulics of Boussinesq and non-Boussinesq two-layer flows. J. Fluid Mech. 215, 457–480.Google Scholar
Luketina, D. A. & Imberger, J. 1987 Characteristics of a surface buoyant jet. J. Geophys. Res. 92, 5435–5447.Google Scholar
MacDonald, D. G. & Chen, F. 2012 Enhancement of turbulence through lateral spreading in a stratified-shear flow: development and assessment of a conceptual model. J. Geophys. Res. 117, C05025.Google Scholar
MacDonald, D. G. & Geyer, W. R. 2005 Hydraulic control of a highly stratified estuarine front. J. Phys. Oceanogr. 35, 374–387.Google Scholar
McCabe, R. M., MacCready, P. & Hickey, B. M. 2009 Ebb-tide dynamics and spreading of a large river plume. J. Phys. Oceanogr. 39, 2839–2856.Google Scholar
de Nijs, M. A. J., Pietrzak, J. D. & Winterwerp, J. C. 2011 Advection of the salt wedge and evolution of the internal flow structure in the Rotterdam Waterway. J. Phys. Oceangr. 41, 3–27.Google Scholar
O’Donnell, J. 1988 A numerical technique to incorporate frontal boundaries in two-dimensional layer models of ocean dynamics. J. Phys. Oceanogr. 18, 1584–1600.Google Scholar
Poggioli, A. R. & Horner-Devine, A. R. 2015 The sensitivity of salt wedge estuaries to channel geometry. J. Phys. Oceanogr. 45, 3169–3183.Google Scholar
Pratt, L. J. 1986 Hydraulic control of sill flow with bottom friction. J. Phys. Oceanogr. 16, 1970–1980.Google Scholar
Princevac, M., Fernando, H. J. S. & Whiteman, C. D. 2005 Turbulent entrainment into natural gravity-driven flows. J. Fluid Mech. 533, 259–268.Google Scholar
Rattray, M. Jr. & Mitsuda, E. 1974 Theoretical analysis of conditions in a salt wedge. Estuar. Coast. Mar. Sci. 2, 375–394.Google Scholar
Schijf, J. B. & Schönfeld, J. C. 1953 Theoretical considerations on the motion of salt and fresh water. In Proceedings of the Minnesota International Hydraulics Convention, pp. 321–333. University of Minnessota.Google Scholar
Shin, J. O., Dalziel, S. B. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.Google Scholar
Stommel, H. & Farmer, H. G. 1952 Abrupt change in width in two-layer open channel flow. J. Mar. Res. 11, 205–214.Google Scholar
Wright, L. D. & Coleman, J. M. 1971 Effluent expansion and interfacial mixing in the presence of a Salt Wedge, Mississippi River Delta. J. Geophys. Res. 76 (36), 8649–8661.Google Scholar
Yellen, B., Woodruff, J. D., Kratz, L. N., Mabee, S. B., Morrison, J. & Martini, A. M. 2014 Source, conveyance and fate of suspended sediments following Hurricane Irene. New England, USA. Geomorphology 226, 124–134.Google Scholar
Yuan, Y., Avener, M. E. & Horner-Devine, A. R. 2011 A two-color optical method for determining layer thickness in two interacting buoyant plumes. Exp. Fluids 50, 1235–1245.Google Scholar
Yuan, Y. & Horner-Devine, A. R. 2013 Laboratory investigation of the impact of lateral spreading on buoyancy flux in a river plume. J. Phys. Oceanogr. 43, 2588–2610.Google Scholar