Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Campagne, Antoine
Gallet, Basile
Moisy, Frédéric
and
Cortet, Pierre-Philippe
2014.
Direct and inverse energy cascades in a forced rotating turbulence experiment.
Physics of Fluids,
Vol. 26,
Issue. 12,
Kim, Sun -Chul
and
Okamoto, Hisashi
2014.
The generalized Proudman–Johnson equation and its singular perturbation problems.
Japan Journal of Industrial and Applied Mathematics,
Vol. 31,
Issue. 3,
p.
541.
Gallet, B.
Campagne, A.
Cortet, P.-P.
and
Moisy, F.
2014.
Scale-dependent cyclone-anticyclone asymmetry in a forced rotating turbulence experiment.
Physics of Fluids,
Vol. 26,
Issue. 3,
Constantin, Peter
Tarfulea, Andrei
and
Vicol, Vlad
2014.
Absence of Anomalous Dissipation of Energy in Forced Two Dimensional Fluid Equations.
Archive for Rational Mechanics and Analysis,
Vol. 212,
Issue. 3,
p.
875.
Lucas, Dan
and
Kerswell, Rich
2014.
Spatiotemporal dynamics in two-dimensional Kolmogorov flow over large domains.
Journal of Fluid Mechanics,
Vol. 750,
Issue. ,
p.
518.
Kim, Sun-Chul
and
Okamoto, Hisashi
2015.
Unimodal patterns appearing in the Kolmogorov flows at large Reynolds numbers.
Nonlinearity,
Vol. 28,
Issue. 9,
p.
3219.
Mishra, Pankaj Kumar
Herault, Johann
Fauve, Stephan
and
Verma, Mahendra K.
2015.
Dynamics of reversals and condensates in two-dimensional Kolmogorov flows.
Physical Review E,
Vol. 91,
Issue. 5,
Hiruta, Yoshiki
and
Toh, Sadayoshi
2015.
Solitary solutions including spatially localized chaos and their interactions in two-dimensional Kolmogorov flow.
Physical Review E,
Vol. 92,
Issue. 6,
Hiruta, Yoshiki
and
Toh, Sadayoshi
2017.
Intermittent direction reversals of moving spatially localized turbulence observed in two-dimensional Kolmogorov flow.
Physical Review E,
Vol. 96,
Issue. 6,
Tsang, Yue-Kin
and
Vanneste, Jacques
2017.
The effect of coherent stirring on the advection–condensation of water vapour.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 473,
Issue. 2202,
p.
20170196.
Tithof, Jeffrey
Suri, Balachandra
Pallantla, Ravi Kumar
Grigoriev, Roman O.
and
Schatz, Michael F.
2017.
Bifurcations in a quasi-two-dimensional Kolmogorov-like flow.
Journal of Fluid Mechanics,
Vol. 828,
Issue. ,
p.
837.
Kim, Sun-Chul
Miyaji, Tomoyuki
and
Okamoto, Hisashi
2017.
Unimodal patterns appearing in the two-dimensional Navier–Stokes flows under general forcing at large Reynolds numbers.
European Journal of Mechanics - B/Fluids,
Vol. 65,
Issue. ,
p.
234.
Alexakis, A.
and
Biferale, L.
2018.
Cascades and transitions in turbulent flows.
Physics Reports,
Vol. 767-769,
Issue. ,
p.
1.
Lepot, Simon
Aumaître, Sébastien
and
Gallet, Basile
2018.
Radiative heating achieves the ultimate regime of thermal convection.
Proceedings of the National Academy of Sciences,
Vol. 115,
Issue. 36,
p.
8937.
Seshasayanan, Kannabiran
and
Alexakis, Alexandros
2018.
Condensates in rotating turbulent flows.
Journal of Fluid Mechanics,
Vol. 841,
Issue. ,
p.
434.
Alexakis, Alexandros
2018.
Three-dimensional instabilities and negative eddy viscosity in thin-layer flows.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Beck, Margaret
Cooper, Eric
and
Spiliopoulos, Konstantinos
2019.
Selection of quasi-stationary states in the Navier–Stokes equation on the torus.
Nonlinearity,
Vol. 32,
Issue. 1,
p.
209.
Miquel, Benjamin
Lepot, Simon
Bouillaut, Vincent
and
Gallet, Basile
2019.
Convection driven by internal heat sources and sinks: Heat transport beyond the mixing-length or “ultimate” scaling regime.
Physical Review Fluids,
Vol. 4,
Issue. 12,
Chen, Zhi-Min
2019.
Instability of two-dimensional square eddy flows.
Physics of Fluids,
Vol. 31,
Issue. 4,
Zhang, Jun
Tian, Peng
Yao, Siqi
and
Fei, Fei
2019.
Multiscale investigation of Kolmogorov flow: From microscopic molecular motions to macroscopic coherent structures.
Physics of Fluids,
Vol. 31,
Issue. 8,
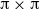 $\lrm{\pi} \ensuremath{\times} \lrm{\pi} $ square box with stress-free boundary conditions. The flow is steadily forced by the addition of a source
$\lrm{\pi} \ensuremath{\times} \lrm{\pi} $ square box with stress-free boundary conditions. The flow is steadily forced by the addition of a source 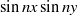 $\sin nx\sin ny$ to the vorticity equation; attention is restricted to even
$\sin nx\sin ny$ to the vorticity equation; attention is restricted to even  $n$ so that the forcing has zero integral. Numerical solutions with
$n$ so that the forcing has zero integral. Numerical solutions with 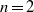 $n= 2$ and
$n= 2$ and 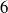 $6$ show that at high Reynolds numbers the solution is a domain-scale vortex condensate with a strong projection on the gravest mode,
$6$ show that at high Reynolds numbers the solution is a domain-scale vortex condensate with a strong projection on the gravest mode, 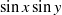 $\sin x\sin y$. The sign of the vortex condensate is selected by a symmetry-breaking instability. We show that the amplitude of the vortex condensate has a finite limit as
$\sin x\sin y$. The sign of the vortex condensate is selected by a symmetry-breaking instability. We show that the amplitude of the vortex condensate has a finite limit as 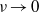 $\nu \ensuremath{\rightarrow} 0$. Using a quasilinear approximation we make an analytic prediction of the amplitude of the condensate and show that the amplitude is determined by viscous selection of a particular solution from a family of solutions to the forced two-dimensional Euler equation. This theory indicates that the condensate amplitude will depend sensitively on the form of the dissipation, even in the undamped limit. This prediction is verified by considering the addition of a drag term to the Navier–Stokes equation and comparing the quasilinear theory with numerical solution.
$\nu \ensuremath{\rightarrow} 0$. Using a quasilinear approximation we make an analytic prediction of the amplitude of the condensate and show that the amplitude is determined by viscous selection of a particular solution from a family of solutions to the forced two-dimensional Euler equation. This theory indicates that the condensate amplitude will depend sensitively on the form of the dissipation, even in the undamped limit. This prediction is verified by considering the addition of a drag term to the Navier–Stokes equation and comparing the quasilinear theory with numerical solution.