Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T11:25:52.517Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional phoretic swimmers: the singular weak-advection limits

Published online by Cambridge University Press:  10 March 2017

Ehud Yariv Open the ORCID record for Ehud Yariv [Opens in a new window]
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Because of the associated far-field logarithmic divergence, the transport problem governing two-dimensional phoretic self-propulsion lacks a steady solution when the Péclet number 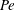$\mathit{Pe}$ vanishes. This indeterminacy, which has no counterpart in three dimensions, is remedied by introducing a non-zero value of 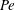$\mathit{Pe}$, however small. We consider that problem employing a first-order kinetic model of solute absorption, where the ratio of the characteristic magnitudes of reaction and diffusion is quantified by the Damköhler number 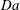$\mathit{Da}$. As 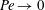$\mathit{Pe}\rightarrow 0$ the dominance of diffusion breaks down at distances that scale inversely with 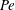$\mathit{Pe}$; at these distances, the leading-order transport represents a two-dimensional point source in a uniform stream. Asymptotic matching between the latter region and the diffusion-dominated near-particle region provides the leading-order particle velocity as an implicit function of 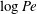$\log \mathit{Pe}$. Another scenario involving weak advection takes place under strong reactions, where 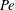$\mathit{Pe}$ and 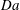$\mathit{Da}$ are large and comparable. In that limit, the breakdown of diffusive dominance occurs at distances that scale as 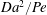$\mathit{Da}^{2}/\mathit{Pe}$.

JFM classification

Complex Fluids: Colloids Complex Fluids: Complex Fluids Low-Reynolds-number flows: Low-Reynolds-number flows
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , R3
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A. & Taylor, T. D. 1962 Heat and mass transfer from single spheres in Stokes flow. Phys. Fluids 5 (4), 387–394.Google Scholar
Anderson, J. L. 1989 Colloid transport by interfacial forces. Annu. Rev. Fluid Mech. 30, 139–165.Google Scholar
Bechinger, C., Di Leonardo, R., Löwen, H., Reichhardt, C., Volpe, G. & Volpe, G. 2016 Active particles in complex and crowded environments. Rev. Mod. Phys. 88 (4), 045006-50.Google Scholar
Blake, J. R. 1971 Self propulsion due to oscillations on the surface of a cylinder at low Reynolds number. Bull. Austral. Math. Soc. 5 (2), 255–264.CrossRefGoogle Scholar
Crowdy, D. G. 2013 Wall effects on self-diffusiophoretic Janus particles: a theoretical study. J. Fluid Mech. 735, 473–498.Google Scholar
Crowdy, D. G. & Or, Y. 2010 Two-dimensional point singularity model of a low-Reynolds-number swimmer near a wall. Phys. Rev. E 81 (3), 036313.Google ScholarPubMed
Crowdy, D. & Samson, O. 2011 Hydrodynamic bound states of a low-Reynolds-number swimmer near a gap in a wall. J. Fluid Mech. 667, 309–335.Google Scholar
Davis, A. M. J. & Crowdy, D. G. 2012 Stresslet asymptotics for a treadmilling swimmer near a two-dimensional corner: hydrodynamic bound states. Proc. R. Soc. Lond. A 468 (2148), 3765–3783.Google Scholar
Davis, A. M. J. & Crowdy, D. G. 2013 Matched asymptotics for a treadmilling low-Reynolds-number swimmer near a wall. Q. J. Mech. Appl. Maths 66 (1), 53–73.Google Scholar
Ebbens, S., Tu, M.-H., Howse, J. R. & Golestanian, R. 2012 Size dependence of the propulsion velocity for catalytic Janus-sphere swimmers. Phys. Rev. E 85 (2), 020401.Google ScholarPubMed
Golestanian, R., Liverpool, T. B. & Ajdari, A. 2007 Designing phoretic micro-and nano-swimmers. New J. Phys. 9, 126.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Howse, J. R., Jones, R. A. L., Ryan, A. J., Gough, T., Vafabakhsh, R. & Golestanian, R. 2007 Self-motile colloidal particles: from directed propulsion to random walk. Phys. Rev. Lett. 99 (4), 048102.Google Scholar
Lauga, E. & Powers, T. R. 2009 The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 72 (9), 096601.CrossRefGoogle Scholar
Lighthill, M. J. 1952 On the squirming motion of nearly spherical deformable bodies through liquids at very small Reynolds numbers. Commun. Pure Appl. Maths 5 (2), 109–118.Google Scholar
Michelin, S. & Lauga, E. 2014 Phoretic self-propulsion at finite Péclet numbers. J. Fluid Mech. 747, 572–604.Google Scholar
Michelin, S., Lauga, E. & Bartolo, D. 2013 Spontaneous autophoretic motion of isotropic particles. Phys. Fluids 25 (6), 061701.Google Scholar
Saffman, P. G. & Delbrück, M. 1975 Brownian motion in biological membranes. Proc. Natl Acad. Sci. USA 72 (8), 3111–3113.Google Scholar
Sondak, D., Hawley, C., Heng, S., Vinsonhaler, R., Lauga, E. & Thiffeault, J.-L. 2016 Can phoretic particles swim in two dimensions? Phys. Rev. E 94 (6), 062606.Google Scholar
Squires, T. M. & Bazant, M. Z. 2006 Breaking symmetries in induced-charge electro-osmosis and electrophoresis. J. Fluid Mech. 560, 65–101.Google Scholar
Taylor, G. I. 1951 Analysis of the swimming of microscopic organisms. Proc. R. Soc. Lond. A 209 (1099), 447–461.Google Scholar
Yariv, E. & Kaynan, U. 2017 Phoretic drag reduction of chemically active homogeneous spheres under force fields and shear flows. Phys. Rev. Fluids 2 (1), 012201.Google Scholar
Yariv, E. & Michelin, S. 2015 Phoretic self-propulsion at large Péclet numbers. J. Fluid Mech. 768, R1.Google Scholar
Zöttl, A. & Stark, H. 2016 Emergent behavior in active colloids. J. Phys.: Condens. Matter 28 (25), 1–28.Google Scholar