Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T19:33:01.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional magnetohydrodynamic turbulence in the small magnetic Prandtl number limit

Published online by Cambridge University Press:  14 June 2012

David G. Dritschel  and
Steven M. Tobias
David G. Dritschel
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
Steven M. Tobias*
Affiliation:
Department of Applied Mathematics, University of Leeds, Leeds LS2 9JT, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

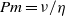In this paper we introduce a new method for computations of two-dimensional magnetohydrodynamic (MHD) turbulence at low magnetic Prandtl number . When , the magnetic field dissipates at a scale much larger than the velocity field. The method we utilize is a novel hybrid contour–spectral method, the ‘combined Lagrangian advection method’, formally to integrate the equations with zero viscous dissipation. The method is compared with a standard pseudo-spectral method for decreasing 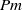for the problem of decaying two-dimensional MHD turbulence. The method is shown to agree well for a wide range of imposed magnetic field strengths. Examples of problems for which such a method may prove invaluable are also given.

JFM classification

Mathematical Foundations: Computational methods MHD and Electrohydrodynamics: MHD turbulence Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 703 , 25 July 2012 , pp. 85 - 98
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids 12, 233–239.CrossRefGoogle Scholar
2. Biskamp, D. 2003 Magnetohydrodynamic Turbulence. Cambridge University Press.CrossRefGoogle Scholar
3. Biskamp, D. & Welter, H. 1989 Dynamics of decaying two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1, 1964–1979.CrossRefGoogle Scholar
4. Brandenburg, A. & Nordlund, Å 2011 Astrophysical turbulence modelling. Rep. Prog. Phys. 74, 046901.CrossRefGoogle Scholar
5. Cattaneo, F. & Tobias, S. M. 2005 Interaction between dynamos at different scales. Phys. Fluids 17, 127105.CrossRefGoogle Scholar
6. Cattaneo, F. & Vainshtein, S. I. 1991 Suppression of turbulent transport by a weak magnetic field. Astrophys. J. 376, L21.CrossRefGoogle Scholar
7. Diamond, P. H., Itoh, S.-I., Itoh, K. & Silvers, L. J. 2007 -plane MHD turbulence and dissipation in the solar tachocline. In The Solar Tachocline (ed. Hughes, D. W., Rosner, R. & Weiss, N. O. ), p. 213. Cambridge University Press.CrossRefGoogle Scholar
8. Dritschel, D. G. & Ambaum, M. H. P. 1997 A contour-advective semi-Lagrangian numerical algorithm for simulating fine-scale conservative dynamical fields. Q. J. R. Meteorol. Soc. 123, 1097–1130.Google Scholar
9. Dritschel, D. G. & Fontane, J. 2010 The combined Lagrangian advection method. J. Comput. Phys. 229, 5408–5417.CrossRefGoogle Scholar
10. Dritschel, D. G. & McIntyre, M. E. 2008 Multiple jets as PV staircases: the Phillips effect and the resilience of eddy-transport barriers. J. Atmos. Sci. 65, 855–874.CrossRefGoogle Scholar
11. Dritschel, D. G. & Scott, R. K. 2009 On the simulation of nearly inviscid two-dimensional turbulence. J. Comput. Phys. 228, 2707–2711.CrossRefGoogle Scholar
12. Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008a Unifying scaling theory for vortex dynamics in two-dimensional turbulence. Phys. Rev. Lett. 101 (9), 094501.CrossRefGoogle ScholarPubMed
13. Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008b Late time evolution of unforced inviscid two-dimensional turbulence. J. Fluid Mech. 640, 215–233.CrossRefGoogle Scholar
14. Dritschel, D. G. & Viúdez, Á. 2003 A balanced approach to modelling rotating stably stratified geophysical flows. J. Fluid Mech. 488, 123–150.CrossRefGoogle Scholar
15. Fontane, J. & Dritschel, D. G. 2009 The HyperCASL algorithm: a new approach to the numerical simulation of geophysical flows. J. Comput. Phys. 228, 6411–6425.CrossRefGoogle Scholar
16. Gill, A. E. 1982 Atmosphere-Ocean Dynamics. Academic.Google Scholar
17. Gilman, P. A. 2000 Magnetohydrodynamic ‘Shallow Water’ equations for the solar tachocline. Astrophys. J. 544, L79–82.CrossRefGoogle Scholar
18. Gough, D. O. 2007 An introduction to the solar tachocline. In The Solar Tachocline (ed. Hughes, D. W., Rosner, R. & Weiss, N. O. ), p. 3 Cambridge University Press.CrossRefGoogle Scholar
19. Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential-vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946.CrossRefGoogle Scholar
20. Iroshnikov, P. S. 1967 Turbulence of a conducting fluid in a strong magnetic field. Sov. Astron. 7, 566–571.Google Scholar
21. Kraichnan, R. H. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385–1387.CrossRefGoogle Scholar
22. Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.CrossRefGoogle Scholar
23. McKiver, W. & Dritschel, D. G. 2008 Balance in non-hydrostatic rotating stratified turbulence. J. Fluid Mech. 596, 201–219.CrossRefGoogle Scholar
24. Miesch, M. S. 2005 Large-scale dynamics of the convection zone and tachocline. Living Rev. Solar Phys. 2, 1.CrossRefGoogle Scholar
25. Ossendrijver, M. 2003 The solar dynamo. Astron. Astrophys. Rev. 11, 287–367.CrossRefGoogle Scholar
26. Schekochihin, A. A., Haugen, N. E. L., Brandenburg, A., Cowley, S. C., Maron, J. L. & McWilliams, J. C. 2005 The onset of a small-scale turbulent dynamo at low magnetic Prandtl numbers. Astrophys. J. 625, L115–L118.CrossRefGoogle Scholar
27. Tobias, S. M. 2005 The solar tachocline: formation, stability and its role in the solar dynamo. In Fluid Dynamics and Dynamos in Astrophysics and Geophysics (ed. Soward, A. M., Jones, C. A., Hughes, D. W. & Weiss, N. O. ), p. 193. CRC.Google Scholar
28. Tobias, S. M. 2010 The solar tachocline: a strudy in stably stratified MHD turbulence. In IUTAM Symposium on Turbulence in the Atmosphere and Oceans (ed. Dritschel, D. G. ), pp. 169–179. Springer.CrossRefGoogle Scholar
29. Tobias, S. M. & Cattaneo, F. 2008 Dynamo action in complex flows: the quick and the fast. J. Fluid Mech. 601, 101–122.CrossRefGoogle Scholar
30. Tobias, S. M., Cattaneo, F. & Boldyrev, S. 2012 MHD dynamos & turbulence. In The Nature of Turbulence. Cambridge University Press.Google Scholar
31. Tobias, S. M., Dagon, K. & Marston, J. B. 2011 Astrophysical fluid dynamics via direct statistical simulation. Astrophys. J. 727, 127.CrossRefGoogle Scholar
32. Tobias, S. M., Diamond, P. H. & Hughes, D. W. 2007 -plane magnetohydrodynamic turbulence in the solar tachocline. Astrophys. J. 667, L113–L116.CrossRefGoogle Scholar
33. Tobias, S. & Weiss, N. 2007 The solar dynamo and the tachocline. In The Solar Tachocline (ed. Hughes, D. W., Rosner, R. & Weiss, N. O. ), pp. 319–350. Cambridge University Press.CrossRefGoogle Scholar
34. Weiss, N. O. 1966 The expulsion of magnetic flux by eddies. Proc. R. Soc. Lond. A 293, 310–328.Google Scholar
35. Wood, T. S. & McIntyre, M. E. 2011 Polar confinement of the Sun’s interior magnetic field by laminar magnetostrophic flow. J. Fluid Mech. 677, 445–482.CrossRefGoogle Scholar