Article contents
Two-dimensional gravity–capillary solitary waves on deep water: generation and transverse instability
Published online by Cambridge University Press: 17 November 2017
Abstract
Two-dimensional (2-D) gravity–capillary solitary waves are generated using a moving pressure jet from a 2-D narrow slit as a forcing onto the surface of deep water. The forcing moves horizontally over the surface of the deep water at speeds close to the minimum phase speed 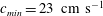 $c_{min}=23~\text{cm}~\text{s}^{-1}$. Four different states are observed according to the forcing speed. At relatively low speeds below
$c_{min}=23~\text{cm}~\text{s}^{-1}$. Four different states are observed according to the forcing speed. At relatively low speeds below  $c_{min}$, small-amplitude depressions are observed and they move steadily just below the moving forcing. As the forcing speed increases towards
$c_{min}$, small-amplitude depressions are observed and they move steadily just below the moving forcing. As the forcing speed increases towards 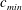 $c_{min}$, nonlinear 2-D gravity–capillary solitary waves are observed, and they move steadily behind the moving forcing. When the forcing speed is very close to
$c_{min}$, nonlinear 2-D gravity–capillary solitary waves are observed, and they move steadily behind the moving forcing. When the forcing speed is very close to 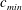 $c_{min}$, periodic shedding of a 2-D local depression is observed behind the moving forcing. Finally, at relatively high speeds above
$c_{min}$, periodic shedding of a 2-D local depression is observed behind the moving forcing. Finally, at relatively high speeds above 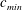 $c_{min}$, a pair of short and long linear waves is observed, respectively ahead of and behind the moving forcing. In addition, we observe the transverse instability of free 2-D gravity–capillary solitary waves and, further, the resultant formation of three-dimensional gravity–capillary solitary waves. These experimental observations are compared with numerical results based on a model equation that admits gravity–capillary solitary wave solutions near
$c_{min}$, a pair of short and long linear waves is observed, respectively ahead of and behind the moving forcing. In addition, we observe the transverse instability of free 2-D gravity–capillary solitary waves and, further, the resultant formation of three-dimensional gravity–capillary solitary waves. These experimental observations are compared with numerical results based on a model equation that admits gravity–capillary solitary wave solutions near 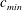 $c_{min}$. They agree with each other very well. In particular, based on a linear stability analysis, we give a theoretical proof for the transverse instability of the 2-D gravity–capillary solitary waves on deep water.
$c_{min}$. They agree with each other very well. In particular, based on a linear stability analysis, we give a theoretical proof for the transverse instability of the 2-D gravity–capillary solitary waves on deep water.
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 11
- Cited by



