Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Qin, Bin
Alam, Md. Mahbub
Ji, Chunning
Liu, Yang
and
Xu, Shengjin
2018.
Flow-induced vibrations of two cylinders of different natural frequencies.
Ocean Engineering,
Vol. 155,
Issue. ,
p.
189.
Zhang, Meihua
and
Zheng, Zhongquan C.
2018.
Relations of POD modes and Lyapunov exponents to the nonlinear dynamic states in flow over oscillating tandem cylinders.
Physics of Fluids,
Vol. 30,
Issue. 12,
p.
123602.
Alam, Md. Mahbub
Elhimer, Mehdi
Wang, Longjun
Jacono, David Lo
and
Wong, C. W.
2018.
Vortex shedding from tandem cylinders.
Experiments in Fluids,
Vol. 59,
Issue. 3,
Zafar, Farhan
and
Alam, Md. Mahbub
2018.
A low Reynolds number flow and heat transfer topology of a cylinder in a wake.
Physics of Fluids,
Vol. 30,
Issue. 8,
Zhu, Hongjun
Zhang, Chun
and
Liu, Wenli
2019.
Wake-induced vibration of a circular cylinder at a low Reynolds number of 100.
Physics of Fluids,
Vol. 31,
Issue. 7,
Derakhshandeh, J.F.
and
Alam, Md Mahbub
2019.
A review of bluff body wakes.
Ocean Engineering,
Vol. 182,
Issue. ,
p.
475.
Yang, Wenchao
and
Stremler, Mark A.
2019.
Critical spacing of stationary tandem circular cylinders at Re≈100.
Journal of Fluids and Structures,
Vol. 89,
Issue. ,
p.
49.
Wang, Qing-Yang
Xu, Sheng-Jin
Gan, Lian
Zhang, Wei-Guo
and
Zhou, Yu
2019.
Scaling of the time-mean characteristics in the polygonal cylinder near-wake.
Experiments in Fluids,
Vol. 60,
Issue. 12,
Zhu, Hongjun
and
Zhou, Tongming
2019.
Flow around a circular cylinder attached with a pair of fin-shaped strips.
Ocean Engineering,
Vol. 190,
Issue. ,
p.
106484.
Zhou, Qiang
Alam, Md. Mahbub
Cao, Shuyang
Liao, Haili
and
Li, Mingshui
2019.
Numerical study of wake and aerodynamic forces on two tandem circular cylinders at Re = 103.
Physics of Fluids,
Vol. 31,
Issue. 4,
Liu, Minghou
Xie, Chen
Yang, Jianzhi
Zhu, Xiaowei
and
Yao, Mengyun
2019.
Numerical study on the flow over two circular disks in tandem arrangement.
Physics of Fluids,
Vol. 31,
Issue. 3,
Liu, Feng-Rui
Zhang, Wen-Ming
Zhao, Lin-Chuan
Zou, Hong-Xiang
Tan, Ting
Peng, Zhi-Ke
and
Meng, Guang
2020.
Performance enhancement of wind energy harvester utilizing wake flow induced by double upstream flat-plates.
Applied Energy,
Vol. 257,
Issue. ,
p.
114034.
Zhu, Hongjun
Tan, Xiaonian
Gao, Yun
Zhou, Tongming
and
Liu, Wenli
2020.
Two-degree-of-freedom flow-induced vibration of two rigidly coupled tandem cylinders of unequal diameters.
Ocean Engineering,
Vol. 216,
Issue. ,
p.
108142.
Alam, Md. Mahbub
Abdelhamid, Talaat
and
Sohankar, Ahmad
2020.
Effect of cylinder corner radius and attack angle on heat transfer and flow topology.
International Journal of Mechanical Sciences,
Vol. 175,
Issue. ,
p.
105566.
Chen, Zhenlin
Alam, Md. Mahbub
Qin, Bin
and
Zhou, Yu
2020.
Energy harvesting from and vibration response of different diameter cylinders.
Applied Energy,
Vol. 278,
Issue. ,
p.
115737.
Zafar, Farhan
and
Alam, Md. Mahbub
2020.
Mixed convection heat transfer from a circular cylinder submerged in wake.
International Journal of Mechanical Sciences,
Vol. 183,
Issue. ,
p.
105733.
Bakhtiari, A.
Zeinoddini, M.
Ashrafipour, H.
Tamimi, V.
Harandi, M.M. Aalami
and
Jadidi, P.
2020.
The effects of marine fouling on the wake-induced vibration of tandem circular cylinders.
Ocean Engineering,
Vol. 216,
Issue. ,
p.
108093.
Shi, Xiaoyu
Alam, Mahbub
and
Bai, Honglei
2020.
Wakes of elliptical cylinders at low Reynolds number.
International Journal of Heat and Fluid Flow,
Vol. 82,
Issue. ,
p.
108553.
Rastan, M. R.
and
Alam, Md. Mahbub
2021.
Transition of wake flows past two circular or square cylinders in tandem.
Physics of Fluids,
Vol. 33,
Issue. 8,
Rajpoot, Rajendra S.
Anirudh, K.
and
Dhinakaran, S.
2021.
Numerical investigation of unsteady flow across tandem square cylinders near a moving wall at Re = 100.
Case Studies in Thermal Engineering,
Vol. 26,
Issue. ,
p.
101042.
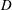 $D$ placed in the wake of another circular cylinder with a smaller diameter of
$D$ placed in the wake of another circular cylinder with a smaller diameter of 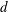 $d$ is investigated, including the time-mean drag coefficient (
$d$ is investigated, including the time-mean drag coefficient (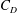 $C_{D}$), the fluctuating drag and lift coefficients (
$C_{D}$), the fluctuating drag and lift coefficients (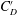 $C_{D}^{\prime }$ and
$C_{D}^{\prime }$ and 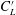 $C_{L}^{\prime }$), the Strouhal number (
$C_{L}^{\prime }$), the Strouhal number (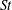 $St$) and the flow structures. The Reynolds number based on
$St$) and the flow structures. The Reynolds number based on 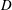 $D$ is kept constant at
$D$ is kept constant at 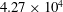 $4.27\times 10^{4}$. The ratios
$4.27\times 10^{4}$. The ratios 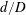 $d/D$ and
$d/D$ and 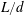 $L/d$ vary from 0.2 to 1.0 and 1.0 to 8.0 respectively, where
$L/d$ vary from 0.2 to 1.0 and 1.0 to 8.0 respectively, where 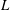 $L$ is the distance from the upstream cylinder centre to the forward stagnation point of the downstream cylinder. The ratios
$L$ is the distance from the upstream cylinder centre to the forward stagnation point of the downstream cylinder. The ratios 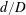 $d/D$ and
$d/D$ and 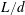 $L/d$ are found, based on extensive hotwire, particle imaging velocimetry, pressure and flow visualization measurements, to have a marked influence on the wake dynamics behind the cylinders. As such, the flow is classified into the reattachment and co-shedding flow regimes, the latter being further subdivided into the lock-in, subharmonic lock-in and no lock-in regions. It is found that the critical spacing that divides the two regimes is dictated by the upstream-cylinder vortex formation length and becomes larger for smaller
$L/d$ are found, based on extensive hotwire, particle imaging velocimetry, pressure and flow visualization measurements, to have a marked influence on the wake dynamics behind the cylinders. As such, the flow is classified into the reattachment and co-shedding flow regimes, the latter being further subdivided into the lock-in, subharmonic lock-in and no lock-in regions. It is found that the critical spacing that divides the two regimes is dictated by the upstream-cylinder vortex formation length and becomes larger for smaller 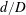 $d/D$. The characteristic flow properties are documented in each regime and subdivided region, including the flow structure,
$d/D$. The characteristic flow properties are documented in each regime and subdivided region, including the flow structure, 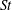 $St$, wake width, vortex formation length and the lateral width between the two gap shear layers. The variations in
$St$, wake width, vortex formation length and the lateral width between the two gap shear layers. The variations in 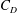 $C_{D}$,
$C_{D}$, 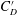 $C_{D}^{\prime }$,
$C_{D}^{\prime }$, 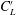 $C_{L}^{\prime }$ and the pressure distribution around the downstream cylinder are connected to the flow physics.
$C_{L}^{\prime }$ and the pressure distribution around the downstream cylinder are connected to the flow physics.