Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T09:26:29.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Two- and three-dimensional instabilities in the wake of a circular cylinder near a moving wall

Published online by Cambridge University Press:  05 January 2017

Hongyi Jiang ,
Liang Cheng ,
Scott Draper  and
Hongwei An
Hongyi Jiang*
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Liang Cheng
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
Scott Draper
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia Centre for Offshore Foundation Systems, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
Hongwei An
Affiliation:
School of Civil, Environmental and Mining Engineering, The University of Western Australia, 35 Stirling Highway, Crawley, WA 6009, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

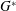Two-dimensional (2D) and three-dimensional (3D) instabilities in the wake of a circular cylinder placed near to a moving wall are investigated using direct numerical simulation (DNS). The study covers a parameter space spanning a non-dimensional gap ratio ($G^{\ast }$) between 0.1 to 19.5 and Reynolds number (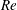$Re$) up to 300. Variations in the flow characteristics with 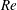$Re$ and 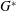$G^{\ast }$ are studied, and their correlations with the hydrodynamic forces on the cylinder are investigated. It is also found that the monotonic increase of the critical 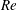$Re$ for 2D instability (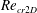$Re_{cr2D}$) with decreasing 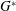$G^{\ast }$ is influenced by variations in the mean flow rate around the cylinder, the confinement of the near-wake flow by the plane wall and the characteristics of the shear layer formed above the moving wall directly below the cylinder. The first factor destabilizes the wake flow at a moderate 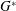$G^{\ast }$ while the latter two factors stabilize the wake flow with decreasing 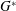$G^{\ast }$. In terms of 3D instability, the flow transition sequence of ‘2D steady 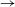$\rightarrow$ 3D steady 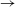$\rightarrow$ 3D unsteady’ for small gap ratios is analysed at 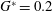$G^{\ast }=0.2$. It is found that the 3D steady and 3D unsteady flows are triggered by Mode C instability due to wall proximity. However, the Mode C structure is not sustained indefinitely, since interference with the shear layer leads to other 3D steady and unsteady flow structures.

JFM classification

Vortex Flows: Vortex instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 435 - 462
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Biancofiore, L. & Gallaire, F. 2012 Counterpropagating Rossby waves in confined plane wakes. Phys. Fluids 24, 074102.Google Scholar
Biancofiore, L., Gallaire, F. & Pasquetti, R. 2011 Influence of confinement on a two-dimensional wake. J. Fluid Mech. 688, 297–320.CrossRefGoogle Scholar
Blackburn, H. M. & Sheard, G. J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22, 031701.Google Scholar
Carmo, B. S., Sherwin, S. J., Bearman, P. W. & Willden, R. H. J. 2008 Wake transition in the flow around two circular cylinders in staggered arrangements. J. Fluid Mech. 597, 1–29.CrossRefGoogle Scholar
Drazin, P. G. 2002 Introduction to Hydrodynamic Stability. Cambridge University Press.Google Scholar
Henderson, R. D. 1995 Details of the drag curve near the onset of vortex shedding. Phys. Fluids 7, 2102.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Huang, W. X. & Sung, H. J. 2007 Vortex shedding from a circular cylinder near a moving wall. J. Fluids Struct. 23, 1064–1076.Google Scholar
Issa, R. I. 1986 Solution of implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 62, 40–65.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jiang, H., Cheng, L., Draper, S., An, H. & Tong, F. 2016a Three-dimensional direct numerical simulation of wake transitions of a circular cylinder. J. Fluid Mech. 801, 353–391.Google Scholar
Jiang, H., Cheng, L., Tong, F., Draper, S. & An, H. 2016b Stable state of Mode A for flow past a circular cylinder. Phys. Fluids 28, 104103.Google Scholar
Juniper, M. P. 2006 The effect of confinement on the stability of two-dimensional shear flows. J. Fluid Mech. 565, 171–195.Google Scholar
Lei, C., Cheng, L., Armfield, S. W. & Kavanagh, K. 2000 Vortex shedding suppression for flow over a circular cylinder near a plane boundary. Ocean Engng 27, 1109–1127.CrossRefGoogle Scholar
Posdziech, O. & Grundmann, R. 2001 Numerical simulation of the flow around an infinitely long circular cylinder in the transition regime. Theor. Comput. Fluid Dyn. 15, 121–141.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013b The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2015 Flow past a rotating cylinder translating at different gap heights along a wall. J. Fluids Struct. 57, 314–330.Google Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.Google Scholar
Taneda, S. 1965 Experimental investigation of vortex streets. J. Phys. Soc. Japan 20, 1714–1721.CrossRefGoogle Scholar
Thapa, J., Zhao, M., Zhou, T. & Cheng, L. 2014 Three-dimensional simulation of vortex shedding flow in the wake of a yawed circular cylinder near a plane boundary at a Reynolds number of 500. Ocean Engng 87, 25–39.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.Google Scholar
Williamson, C. H. K. 1996 Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Wu, M. H., Wen, C. Y., Yen, R. H., Weng, M. C. & Wang, A. B. 2004 Experimental and numerical study of the separation angle for flow around a circular cylinder at low Reynolds number. J. Fluid Mech. 515, 233–260.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013a Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013b Energy contents and vortex dynamics in Mode-C transition of wired-cylinder wake. Phys. Fluids 25, 054103.Google Scholar
Yoon, H. S., Lee, J. B., Seo, J. H. & Park, H. S. 2010 Characteristics for flow and heat transfer around a circular cylinder near a moving wall in wide range of low Reynolds number. Intl J. Heat Mass Transfer 53, 5111–5120.Google Scholar
Zdravkovich, M. M. 1985 Observation of vortex shedding behind a towed circular cylinder near a wall. In Proceedings of the 3rd International Symposium on Flow Visualization, Ann Arbor, Michigan, pp. 423–427. Hemisphere.Google Scholar
Zhang, H. Q., Fey, U., Noack, B. R., König, M. & Eckelmann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7, 779–794.Google Scholar