Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-17T07:24:23.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent temperature fluctuations in a closed Rayleigh–Bénard convection cell

Published online by Cambridge University Press:  04 July 2019

Yin Wang Open the ORCID record for Yin Wang [Opens in a new window] ,
Xiaozhou He  and
Penger Tong Open the ORCID record for Penger Tong [Opens in a new window]
Yin Wang
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
Xiaozhou He
Affiliation:
School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen, China
Penger Tong*
Affiliation:
Department of Physics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, Hong Kong
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

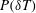We report a systematic study of spatial variations of the probability density function (PDF) $P(\unicode[STIX]{x1D6FF}T)$ for temperature fluctuations 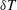$\unicode[STIX]{x1D6FF}T$ in turbulent Rayleigh–Bénard convection along the central axis of two different convection cells. One of the convection cells is a vertical thin disk and the other is an upright cylinder of aspect ratio unity. By changing the distance $z$ away from the bottom conducting plate, we find the functional form of the measured 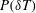$P(\unicode[STIX]{x1D6FF}T)$ in both cells evolves continuously with distinct changes in four different flow regions, namely, the thermal boundary layer, mixing zone, turbulent bulk region and cell centre. By assuming temperature fluctuations in different flow regions are all made from two independent sources, namely, a homogeneous (turbulent) background which obeys Gaussian statistics and non-uniform thermal plumes with an exponential distribution, we obtain the analytic expressions of 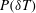$P(\unicode[STIX]{x1D6FF}T)$ in four different flow regions, which are found to be in good agreement with the experimental results. Our work thus provides a unique theoretical framework with a common set of parameters to quantitatively describe the effect of turbulent background, thermal plumes and their spatio-temporal intermittency on the temperature PDF 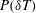$P(\unicode[STIX]{x1D6FF}T)$.

JFM classification

Turbulent Flows: Turbulent convection Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 263 - 284
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Brown, E. & Nikolaenko, A. 2006a Search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.Google Scholar
Ahlers, G., Brown, E., Araujo, F. F., Funfschilling, D., Grossmann, S. & Lohse, D. 2006b Non-Oberbeck-Boussinesq effects in strongly turbulent Rayleigh–Bénard convection. J. Fluid Mech. 569, 409–445.Google Scholar
Arnèodo, A., Benzi, R., Berg, J., Biferale, L., Bodenschatz, E., Busse, A., Calzavarini, E., Castaing, B., Cencini, M., Chevillard, L. et al. 2008 Universal intermittent properties of particle trajectories in highly turbulent flows. Phys. Rev. Lett. 100, 254504.Google Scholar
Ashkenazi, S. & Steinberg, V. 1999 Spectra and statistics of velocity and temperature fluctuations in turbulent convection. Phys. Rev. Lett. 83, 4760–4763.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50, 269–279.Google Scholar
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E 48, R29–R32.Google Scholar
Benzi, R., Tripiccione, R., Massaioli, F., Succi, S. & Cilibertoi, S. 1994 On the scaling of the velocity and temperature structure functions in Rayleigh–Bénard convection. Europhys. Lett. 25, 341–346.Google Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414, 43–164.Google Scholar
Calzavarini, E., Toschi, F. & Tripiccione, R. 2002 Evidences of Bolgiano-Obhukhov scaling in three-dimensional Rayleigh–Bénard convection. Phys. Rev. E 66, 016304.Google Scholar
Camussi, R. & Verzicco, R. 2004 Temporal statistics in high Rayleigh number convective turbulence. Eur. J. Mech. (B/Fluids) 23, 427–442.Google Scholar
Cao, N. & Chen, S. 1997 An intermittency model for passive-scalar turbulence. Phys. Fluids 9, 1203–1205.Google Scholar
Cao, N., Chen, S. & Sreenivasan, K. R. 1996 Scalings of low-order structure functions in fluid turbulence. Phys. Rev. Lett. 77, 3799–3802.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1988 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chertkov, M., Falkovich, G., Kolokolov, I. & Lebedev, V. 1995 Normal and anomalous scaling of 4He fourth-order correlation function of a randomly advected passive scalar. Phys. Rev. E 52, 4924–4941.Google Scholar
Chillá, F., Rastello, M., Chaumat, S. & Castaing, B. 2004 Long relaxation times and tilt sensitivity in Rayleigh–Bénard turbulence. Eur. Phys. J. B 40, 223–227.Google Scholar
Chillá, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Ching, E. S. C. 2007 Measured thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. E 75, 056302.Google Scholar
Ching, E. S. C. & Chau, K. L. 2001 Scaling laws in the central region of confined turbulent thermal convection. Phys. Rev. E 63, 047303.Google Scholar
Ching, E. S. C., Guo, H. & Lo, T. S. 2008 Refined similarity hypotheses in shell models of homogeneous turbulence and turbulent convection. Phys. Rev. E 78, 026303.Google Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1995 Temperature structure functions in turbulent convection at low Prandtl number. Europhys. Lett. E 32, 413–418.Google Scholar
Dimotakis, P. E. 2005 Tubulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Du, Y.-B. & Tong, P. 2001 Temperature fluctuations in a convection cell with rough upper and lower surfaces. Phys. Rev. E 63, 046303.Google Scholar
Gawȩdzki, K. & Kupiainen, A. 1995 Anomalous scaling of the passive scalar. Phys. Rev. Lett. 75, 3834–3837.Google Scholar
Gollub, J. P., Clarke, J., Gharib, M., Lane, B. & Mesquita, O. N. 1991 Fluctuations and transport in a stirred fluid with a mean gradient. Phys. Rev. Lett. 67, 3507–3510.Google Scholar
Grossmann, S. & Lohse, D. 1992 Scaling in hard turbulent Rayleigh–Bénard flow. Phys. Rev. A 46, 903–917.Google Scholar
Grossmann, S. & Lohse, D. 1993 Characteristic scales in Rayleigh–Bénard turbulence. Phys. Lett. A 173, 58–62.Google Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.Google Scholar
He, X.-Z., Ching, E. S. C. & Tong, P. 2011 Locally averaged thermal dissipation rate in turbulent thermal convection: a decomposition into contributions from different temperature gradient components. Phys. Fluids 23, 025106.Google Scholar
He, X.-Z., Shang, X.-D. & Tong, P. 2014 Test of the anomalous scaling of passive temperature fluctuations in turbulent Rayleigh–Bénard convection with spatial inhomogeneity. J. Fluid Mech. 753, 104–130.Google Scholar
He, X.-Z. & Tong, P. 2009 Measurements of the thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. E 79, 026306.Google Scholar
He, X.-Z., Tong, P. & Xia, K.-Q. 2007 Measured thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 144501.Google Scholar
He, X.-Z., Wang, Y. & Tong, P. 2018 Dynamic heterogeneity and conditional statistics of non-Gaussian temperature fluctuations in turbulent thermal convection. Phys. Rev. Fluids. 3, 052401.Google Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
Kerr, R. 1996 Rayleigh number scaling in numerical convection. J. Fluid Mech. 310, 139–179.Google Scholar
Le Borgne, T., Huck, P. D., Dentz, M. & Villermaux, E. 2017 Scalar gradients in stirred mixtures and the deconstruction of random fields. J. Fluid Mech. 812, 578–610.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Mashiko, T., Tsuji, Y., Mizuno, T. & Sano, M. 2004 Instantaneous measurement of velocity fields in developed thermal turbulence in mercury. Phys. Rev. E 69, 036306.Google Scholar
Naert, A., Castaing, B., Chabaud, B., Htbral, B. & Peinke, J. 1998 Conditional statistics of velocity fluctuations in turbulence. Physica D 113, 73–78.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.Google Scholar
Ottino, J. M. 1989 The Kinematics of Mixing: Stretching, Chaos, and Transport. Cambridge University Press.Google Scholar
Paul, E. L., Atiemo-Obeng, V. A. & Kresta, S. M. 2004 Handbook of Industrial Mixing: Science and Practice. Wiley.Google Scholar
Procaccia, I., Ching, E., Constantin, P., Kadanoff, L. P., Libchaber, A. & Wu, X.-Z. 1991 Transitions in convective turbulence: the role of thermal plumes. Phys. Rev. A 44, 8091–8102.Google Scholar
Procaccia, I. & Zeitak, R. 1989 Scaling exponents in nonisotropic convective turbulence. Phys. Rev. Lett. 62, 2128–2131.Google Scholar
Procaccia, I. & Zeitak, R. 1990 Scaling exponents in thermally driven turbulence. Phys. Rev. A 42, 821–830.Google Scholar
Qiu, X.-L. & Tong, P. 2001 Large-scale velocity structures in turbulent thermal convection. Phys. Rev. E 64, 036304.Google Scholar
Sano, M., Wu, X.-Z. & Libchber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40, 6421–6430.Google Scholar
Shang, X.-D., Qiu, X.-L., Tong, P. & Xia, K.-Q 2003 Measured local heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 90, 074501.Google Scholar
She, Z.-S. & Léveque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72, 336–339.Google Scholar
She, Z.-S. & Orszag, S. A. 1991 Physical model of intermittency: inertial-range non-Gaussian statistics. Phys. Rev. Lett. 66, 1701–1704.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1995a Anomalous scaling of a passive scalar in turbulent flow. C. R. Acad. Sci. Paris 321, 279–284.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1995b Scalar turbulence. Nature 405, 639–646.Google Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.Google Scholar
Skrbek, L., Niemela, J. J., Sreenivasan, K. R. & Donnelly, R. J. 2002 Temperature structure functions in the Bolgiano regime of thermal convection. Phys. Rev. E 66, 036303.Google Scholar
Solomon, T. H. & Gollub, J. P. 1991 Thermal boundary layers and heat flux in turbulent convection: the role of recirculating flows. Phys. Rev. A 43, 6683–6693.Google Scholar
Song, H., Villermaux, E. & Tong, P. 2011 Coherent oscillations of turbulent Rayleigh–Bénard convection in a thin vertical disk. Phys. Rev. Lett. 106, 184504.Google Scholar
Sreenivasan, K. R. 1991 Fractals and multifractals in fluid turbulence. Annu. Rev. Fluid Mech. 233, 539–600.Google Scholar
Sreenivasan, K. R. 1991 On local isotropy of passive scalars in turbulent shear flows. Proc. R. Soc. Lond. A 434, 165–182.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421, 79–108.Google Scholar
Takeshita, T., Segawa, T., Glazier, J. A. & Sano, M. 1996 Thermal turbulence in mercury. Phys. Rev. Lett. 76, 1465–1468.Google Scholar
Tong, P. & Shen, Y. 1992 Relative velocity fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 69, 2066–2069.Google Scholar
Villermaux, E. 2012 On dissipation in stirred mixtures. Adv. Appl. Mech. 45, 91–107.Google Scholar
Wang, Y., He, X.-Z. & Tong, P. 2016 Boundary layer fluctuations and their effects on mean and variance temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Fluids 1, 082301.Google Scholar
Wang, Y., Lai, P.-Y., Song, H. & Tong, P. 2018a Mechanism of large-scale flow reversals in turbulent thermal convection. Sci. Adv. 4, 7480.Google Scholar
Wang, Y., Xu, W., He, X.-Z., Yik, H.-F., Wang, X.-P., Schumacher, J. & Tong, P. 2018b Boundary layer fluctuations in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 840, 408–431.Google Scholar
Warhaft, Z. 2000 Passive scalars in turbulent flows. Annu. Rev. Fluid Mech. 32, 203–240.Google Scholar
Wei, P. & Ahlers, G. 2016 On the nature of fluctuations in turbulent Rayleigh–Bénard convection at large Prandtl numbers. J. Fluid Mech. 802, 203–244.Google Scholar
Wilczek, M. 2016 Non-Gaussianity and intermittency in an ensemble of Gaussian fields. New J. Phys. 18, 125009.Google Scholar
Wu, X.-Z., Kadanoff, L. P., Libchaber, A. & Sano, M. 1990 Frequency power spectrum of temperature fluctuations in free convection. Phys. Rev. Lett. 64, 2140–2143.Google Scholar
Wu, X.-Z. & Libchaber, A. 1992 Scaling relations in thermal turbulence: the aspect-ratio dependence. Phys. Rev. A 45, 842–845.Google Scholar
Wu, X.-Z. & Libchaber, A. 1991 Non-Boussinesq effects in free thermal convection. Phys. Rev. A 43, 2833–2839.Google Scholar
Zhang, J., Childress, S. & Libchaber, A. 1997 Non-Boussinesq effect: thermal convection with broken symmetry. Phys. Fluids 9, 1034–1042.Google Scholar
Zhou, Q. & Xia, K.-Q. 2013 Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell. J. Fluid Mech. 721, 199–224.Google Scholar
Zhou, S.-Q. & Xia, K.-Q. 2001 Scaling properties of the temperature field in convective turbulence. Phys. Rev. Lett. 87, 064501.Google Scholar
Zhou, S.-Q. & Xia, K.-Q. 2002 Plume statistics in thermal turbulence: mixing of an active scalar. Phys. Rev. Lett. 89, 184502.Google Scholar