Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-09T22:03:40.321Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent shear-layer mixing: initial conditions, and direct-numerical and large-eddy simulations

Published online by Cambridge University Press:  19 August 2019

Nek Sharan Open the ORCID record for Nek Sharan [Opens in a new window] ,
Georgios Matheou  and
Paul E. Dimotakis
Nek Sharan*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
Georgios Matheou
Affiliation:
Department of Mechanical Engineering, University of Connecticut, Storrs, CT 06269, USA
Paul E. Dimotakis
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Aspects of turbulent shear-layer mixing are investigated over a range of shear-layer Reynolds numbers, 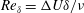$Re_{\unicode[STIX]{x1D6FF}}=\unicode[STIX]{x0394}U\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D708}$, based on the shear-layer free-stream velocity difference, 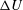$\unicode[STIX]{x0394}U$, and mixing-zone thickness, 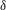$\unicode[STIX]{x1D6FF}$, to probe the role of initial conditions in mixing stages and the evolution of the scalar-field probability density function (p.d.f.) and variance. Scalar transport is calculated for unity Schmidt numbers, approximating gas-phase diffusion. The study is based on direct-numerical simulation (DNS) and large-eddy simulation (LES), comparing different subgrid-scale (SGS) models for incompressible, uniform-density, temporally evolving forced shear-layer flows. Moderate-Reynolds-number DNS results help assess and validate LES SGS models in terms of scalar-spectrum and mixing estimates, as well as other metrics, to 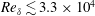$Re_{\unicode[STIX]{x1D6FF}}\lesssim 3.3\times 10^{4}$. High-Reynolds-number LES investigations to 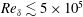$Re_{\unicode[STIX]{x1D6FF}}\lesssim 5\times 10^{5}$ help identify flow parameters and conditions that influence the evolution of scalar variance and p.d.f., e.g. marching versus non-marching. Initial conditions that generate shear flows with different mixing behaviour elucidate flow characteristics in each flow regime and identify elements that induce p.d.f. transition and scalar-variance behaviour. P.d.f. transition is found to be largely insensitive to local flow parameters, such as 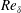$Re_{\unicode[STIX]{x1D6FF}}$, or a previously proposed vortex-pairing parameter based on downstream distance, or other equivalent criteria. The present study also allows a quantitative comparison of LES SGS models in moderate- and high-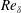$Re_{\unicode[STIX]{x1D6FF}}$ forced shear-layer flows.

JFM classification

Mixing: Turbulent mixing Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 877 , 25 October 2019 , pp. 35 - 81
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almagro, A., García-Villalba, M. & Flores, O. 2017 A numerical study of a variable-density low-speed turbulent mixing layer. J. Fluid Mech. 830, 569–601.10.1017/jfm.2017.583Google Scholar
Arakawa, A. & Lamb, V. R. 1977 Computational design of the basic dynamical processes of the UCLA general circulation model. Meth. Comput. Phys. 17, 173–265.Google Scholar
Attili, A. & Bisetti, F. 2012 Statistics and scaling of turbulence in a spatially developing mixing layer at Re𝜆 = 250. Phys. Fluids 24 (3), 035109.10.1063/1.3696302Google Scholar
Balaras, E., Piomelli, U. & Wallace, J. M. 2001 Self-similar states in turbulent mixing layers. J. Fluid Mech. 446, 1–24.10.1017/S0022112001005626Google Scholar
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.10.1017/S002211205900009XGoogle Scholar
Batt, R. G. 1975 Some measurements on the effect of tripping the two-dimensional shear layer. AIAA J. 13 (2), 245–247.10.2514/3.49681Google Scholar
Batt, R. G. 1977 Turbulent mixing of passive and chemically reacting species in a low-speed shear layer. J. Fluid Mech. 82 (1), 53–95.10.1017/S0022112077000536Google Scholar
Bell, J. H. & Mehta, R. D. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28 (12), 2034–2042.10.2514/3.10519Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (4), 775–816.10.1017/S002211207400190XGoogle Scholar
Carlier, J. & Sodjavi, K. 2016 Turbulent mixing and entrainment in a stratified horizontal plane shear layer: joint velocity–temperature analysis of experimental data. J. Fluid Mech. 806, 542–579.10.1017/jfm.2016.592Google Scholar
Chung, D. & Matheou, G. 2012 Direct numerical simulation of stationary homogeneous stratified sheared turbulence. J. Fluid Mech. 696, 434–467.10.1017/jfm.2012.59Google Scholar
Clark, R. A., Ferziger, J. H. & Reynolds, W. C. 1979 Evaluation of subgrid-scale models using an accurately simulated turbulent flow. J. Fluid Mech. 91 (1), 1–16.10.1017/S002211207900001XGoogle Scholar
Clemens, N. T. & Mungal, M. G. 1995 Large-scale structure and entrainment in the supersonic mixing layer. J. Fluid Mech. 284, 171–216.10.1017/S0022112095000310Google Scholar
Corcos, G. M. & Lin, S. J. 1984 The mixing layer: deterministic models of the turbulent flow. Part 2. The origin of the three-dimensional motion. J. Fluid Mech. 139, 67–95.10.1017/S0022112084000264Google Scholar
Corcos, G. M. & Sherman, F. S. 1984 The mixing layer: deterministic models of the turbulent flow. Part 1. Introduction and the two-dimensional flow. J. Fluid Mech. 139, 29–65.10.1017/S0022112084000252Google Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22 (4), 469–473.10.1063/1.1699986Google Scholar
Cortesi, A. B., Smith, B. L., Sigg, B. & Banerjee, S. 2001 Numerical investigation of the scalar probability density function distribution in neutral and stably stratified mixing layers. Phys. Fluids 13 (4), 927–950.10.1063/1.1352622Google Scholar
Dimotakis, P. E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24 (11), 1791–1796.10.2514/3.9525Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.10.1017/S0022112099007946Google Scholar
Dimotakis, P. E. & Brown, G. L. 1976 The mixing layer at high Reynolds number: large-structure dynamics and entrainment. J. Fluid Mech. 78 (3), 535–560.10.1017/S0022112076002590Google Scholar
Eidson, T. M. 1985 Numerical simulation of the turbulent Rayleigh–Bénard problem using subgrid modelling. J. Fluid Mech. 158, 245–268.10.1017/S0022112085002634Google Scholar
Fiscaletti, D., Attili, A., Bisetti, F. & Elsinga, G. E. 2016 Scale interactions in a mixing layer–the role of the large-scale gradients. J. Fluid Mech. 791, 154–173.10.1017/jfm.2016.53Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 3 (7), 1760–1765.10.1063/1.857955Google Scholar
Hill, D. J., Pantano, C. & Pullin, D. I. 2006 Large-eddy simulation and multiscale modelling of a Richtmyer–Meshkov instability with reshock. J. Fluid Mech. 557, 29–61.10.1017/S0022112006009475Google Scholar
Ho, C.-M. & Huang, L.-S. 1982 Subharmonics and vortex merging in mixing layers. J. Fluid Mech. 119, 443–473.10.1017/S0022112082001438Google Scholar
Huang, L.-S. & Ho, C.-M. 1990 Small-scale transition in a plane mixing layer. J. Fluid Mech. 210, 475–500.10.1017/S0022112090001379Google Scholar
Jahanbakhshi, R. & Madnia, C. K. 2016 Entrainment in a compressible turbulent shear layer. J. Fluid Mech. 797, 564–603.10.1017/jfm.2016.296Google Scholar
Karasso, P. S. & Mungal, M. G. 1996 Scalar mixing and reaction in plane liquid shear layers. J. Fluid Mech. 323, 23–63.10.1017/S0022112096000833Google Scholar
Konrad, J. H.1976 An experimental investigation of mixing in two-dimensional shear flows with applications to diffusion limited chemical reactions. PhD thesis, California Institute of Technology.Google Scholar
Koochesfahani, M. M. & Dimotakis, P. E. 1986 Mixing and chemical reactions in a turbulent liquid mixing layer. J. Fluid Mech. 170, 83–112.10.1017/S0022112086000812Google Scholar
Lesieur, M. & Metais, O. 1996 New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 28 (1), 45–82.10.1146/annurev.fl.28.010196.000401Google Scholar
Liepmann, H. W. & Laufer, J.1947 Investigations of free turbulent mixing. NACA Technical Note No. 1257.Google Scholar
Lilly, D. K.1966a On the application of the eddy viscosity concept in the inertial sub-range of turbulence. NCAR Manuscript No. 123.Google Scholar
Lilly, D. K.1966b The representation of small-scale turbulence in numerical simulation experiments. NCAR Manuscript No. 281.Google Scholar
Lilly, D. K. 1992 A proposed modification of the germano subgrid-scale closure method. Phys. Fluids 4 (3), 633–635.10.1063/1.858280Google Scholar
Lin, S. J. & Corcos, G. M. 1984 The mixing layer: deterministic models of a turbulent flow. Part 3. The effect of plane strain on the dynamics of streamwise vortices. J. Fluid Mech. 141, 139–178.10.1017/S0022112084000781Google Scholar
Matheou, G. & Bowman, K. W. 2016 A recycling method for the large-eddy simulation of plumes in the atmospheric boundary layer. Environ. Fluid Mech. 16 (1), 69–85.10.1007/s10652-015-9413-4Google Scholar
Matheou, G. & Chung, D. 2014 Large-eddy simulation of stratified turbulence. Part II. Application of the stretched-vortex model to the atmospheric boundary layer. J. Atmos. Sci. 71 (12), 4439–4460.10.1175/JAS-D-13-0306.1Google Scholar
Matheou, G., Chung, D., Nuijens, L., Stevens, B. & Teixeira, J. 2011 On the fidelity of large-eddy simulation of shallow precipitating cumulus convection. Mon. Weath. Rev. 139 (9), 2918–2939.10.1175/2011MWR3599.1Google Scholar
Matheou, G. & Dimotakis, P. E. 2016 Scalar excursions in large-eddy simulations. J. Comput. Phys. 327, 97–120.10.1016/j.jcp.2016.08.035Google Scholar
Mattner, T. W. 2011 Large-eddy simulations of turbulent mixing layers using the stretched-vortex model. J. Fluid Mech. 671, 507–534.10.1017/S002211201000580XGoogle Scholar
McMullan, W. A. & Garrett, S. J. 2016 Initial condition effects on large scale structure in numerical simulations of plane mixing layers. Phys. Fluids 28 (1), 015111.10.1063/1.4939835Google Scholar
Meneveau, C., Lund, T. S. & Cabot, W. H. 1996 A lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 319, 353–385.10.1017/S0022112096007379Google Scholar
Métais, O. & Lesieur, M. 1992 Spectral large-eddy simulation of isotropic and stably stratified turbulence. J. Fluid Mech. 239, 157–194.10.1017/S0022112092004361Google Scholar
Michalke, A. 1964 On the inviscid instability of the hyperbolictangent velocity profile. J. Fluid Mech. 19 (4), 543–556.10.1017/S0022112064000908Google Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based subgrid stress model for large-eddy simulation. Phys. Fluids 9 (8), 2443–2454.10.1063/1.869361Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.10.1017/S0022112082001116Google Scholar
Morinishi, Y., Lund, T. S., Vasilyev, O. V. & Moin, P. 1998 Fully conservative higher order finite difference schemes for incompressible flow. J. Comput. Phys. 143 (1), 90–124.10.1006/jcph.1998.5962Google Scholar
Moser, R. D. & Rogers, M. M. 1993 The three-dimensional evolution of a plane mixing layer: pairing and transition to turbulence. J. Fluid Mech. 247 (1), 275–320.10.1017/S0022112093000473Google Scholar
Mungal, M. G. & Dimotakis, P. E. 1984 Mixing and combustion with low heat release in a turbulent shear layer. J. Fluid Mech. 148, 349–382.10.1017/S002211208400238XGoogle Scholar
Oboukhov, A. M. 1949 Structure of the temperature field in turbulent flows. Isv. Geogr. Geophys. Ser. 13, 58–69.Google Scholar
Oster, D. & Wygnanski, I. 1982 The forced mixing layer between parallel streams. J. Fluid Mech. 123, 91–130.10.1017/S0022112082002973Google Scholar
Oster, D., Wygnanski, I., Dziomba, B. & Fiedler, H. 1978 On the effect of initial conditions on the two dimensional turbulent mixing layer. In Structure and Mechanisms of Turbulence I, pp. 48–64. Springer.10.1007/3-540-08765-6_5Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.10.1017/S0022112001006978Google Scholar
Protter, M. H. & Weinberger, H. F. 2012 Maximum Principles in Differential Equations. Springer.Google Scholar
Pullin, D. I. 2000 A vortex-based model for the subgrid flux of a passive scalar. Phys. Fluids 12 (9), 2311–2319.10.1063/1.1287512Google Scholar
Pullin, D. I. & Lundgren, T. S. 2001 Axial motion and scalar transport in stretched spiral vortices. Phys. Fluids 13 (9), 2553–2563.10.1063/1.1388207Google Scholar
Pullin, D. I. & Saffman, P. G. 1994 Reynolds stresses and one-dimensional spectra for a vortex model of homogeneous anisotropic turbulence. Phys. Fluids 6 (5), 1787–1796.10.1063/1.868240Google Scholar
Pullin, D. I. & Saffman, P. G. 1998 Vortex dynamics in turbulence. Annu. Rev. Fluid Mech. 30 (1), 31–51.10.1146/annurev.fluid.30.1.31Google Scholar
Riley, J. J. & Metcalfe, R. W.1980 Direct numerical simulation of a perturbed, turbulent mixing layer. AIAA 18th Aerospace Sciences Meeting. AIAA Paper 80–0274.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6 (2), 903–923.10.1063/1.868325Google Scholar
Roshko, A. 1976 Structure of turbulent shear flows: a new look. AIAA J. 14 (10), 1349–1357.10.2514/3.61477Google Scholar
Schowalter, D. G., Van Van Atta, C. W. & Lasheras, J. C. 1994 A study of streamwise vortex structure in a stratified shear layer. J. Fluid Mech. 281, 247–291.10.1017/S0022112094003101Google Scholar
Schumann, U. 1985 Algorithms for direct numerical simulation of shear-periodic turbulence. In Ninth International Conference on Numerical Methods in Fluid Dynamics, pp. 492–496. Springer.10.1007/3-540-13917-6_187Google Scholar
Sharan, N.2016 Time-stable high-order finite difference methods for overset grids. PhD thesis, University of Illinois at Urbana-Champaign.Google Scholar
Sharan, N., Matheou, G. & Dimotakis, P. E. 2018a Mixing, scalar boundedness, and numerical dissipation in large-eddy simulations. J. Comput. Phys. 369, 148–172.10.1016/j.jcp.2018.05.005Google Scholar
Sharan, N., Pantano, C. & Bodony, D. J. 2018b Time-stable overset grid method for hyperbolic problems using summation-by-parts operators. J. Comput. Phys. 361, 199–230.10.1016/j.jcp.2018.01.049Google Scholar
Shu, C.-W. & Osher, S. 1988 Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77 (2), 439–471.10.1016/0021-9991(88)90177-5Google Scholar
Slessor, M. D., Zhuang, M. & Dimotakis, P. E. 2000 Turbulent shear-layer mixing: growth-rate compressibility scaling. J. Fluid Mech. 414, 35–45.10.1017/S0022112099006977Google Scholar
Slessor, M. D., Bond, C. L. & Dimotakis, P. E. 1998 Turbulent shear-layer mixing at high Reynolds numbers: effects of inflow conditions. J. Fluid Mech. 376, 115–138.10.1017/S0022112098002857Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weath. Rev. 91 (3), 99–164.10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;22.3.CO;2>Google Scholar
Voelkl, T., Pullin, D. I. & Chan, D. C. 2000 A physical-space version of the stretched-vortex subgrid-stress model for large-eddy simulation. Phys. Fluids 12 (7), 1810–1825.10.1063/1.870429Google Scholar
Wygnanski, I. & Fiedler, H. E. 1970 The two-dimensional mixing region. J. Fluid Mech. 41 (2), 327–361.10.1017/S0022112070000630Google Scholar