Article contents
Turbulent mixing due to the Holmboe wave instability at high Reynolds number
Published online by Cambridge University Press: 30 August 2016
Abstract
We consider numerically the transition to turbulence and associated mixing in stratified shear flows with initial velocity distribution 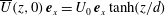 $\overline{U}(z,0)\,\boldsymbol{e}_{x}=U_{0}\,\boldsymbol{e}_{x}\tanh (z/d)$ and initial density distribution
$\overline{U}(z,0)\,\boldsymbol{e}_{x}=U_{0}\,\boldsymbol{e}_{x}\tanh (z/d)$ and initial density distribution 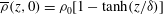 $\overline{\unicode[STIX]{x1D70C}}(z,0)=\unicode[STIX]{x1D70C}_{0}[1-\tanh (z/\unicode[STIX]{x1D6FF})]$ away from a hydrostatic reference state
$\overline{\unicode[STIX]{x1D70C}}(z,0)=\unicode[STIX]{x1D70C}_{0}[1-\tanh (z/\unicode[STIX]{x1D6FF})]$ away from a hydrostatic reference state 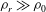 $\unicode[STIX]{x1D70C}_{r}\gg \unicode[STIX]{x1D70C}_{0}$. When the ratio
$\unicode[STIX]{x1D70C}_{r}\gg \unicode[STIX]{x1D70C}_{0}$. When the ratio 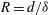 $R=d/\unicode[STIX]{x1D6FF}$ of the characteristic length scales over which the velocity and density vary is equal to one, this flow is primarily susceptible to the classic well-known Kelvin–Helmholtz instability (KHI). This instability, which typically manifests at finite amplitude as an array of elliptical vortices, strongly ‘overturns’ the density interface of strong initial gradient, which nevertheless is the location of minimum initial gradient Richardson number
$R=d/\unicode[STIX]{x1D6FF}$ of the characteristic length scales over which the velocity and density vary is equal to one, this flow is primarily susceptible to the classic well-known Kelvin–Helmholtz instability (KHI). This instability, which typically manifests at finite amplitude as an array of elliptical vortices, strongly ‘overturns’ the density interface of strong initial gradient, which nevertheless is the location of minimum initial gradient Richardson number 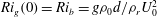 $Ri_{g}(0)=Ri_{b}=g\unicode[STIX]{x1D70C}_{0}d/\unicode[STIX]{x1D70C}_{r}U_{0}^{2}$, where
$Ri_{g}(0)=Ri_{b}=g\unicode[STIX]{x1D70C}_{0}d/\unicode[STIX]{x1D70C}_{r}U_{0}^{2}$, where 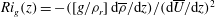 $Ri_{g}(z)=-([g/\unicode[STIX]{x1D70C}_{r}]\,\text{d}\overline{\unicode[STIX]{x1D70C}}/\text{d}z)/(\text{d}\overline{U}/\text{d}z)^{2}$ and
$Ri_{g}(z)=-([g/\unicode[STIX]{x1D70C}_{r}]\,\text{d}\overline{\unicode[STIX]{x1D70C}}/\text{d}z)/(\text{d}\overline{U}/\text{d}z)^{2}$ and 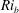 $Ri_{b}$ is a bulk Richardson number. As is well known, at sufficiently high Reynolds numbers (
$Ri_{b}$ is a bulk Richardson number. As is well known, at sufficiently high Reynolds numbers (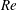 $Re$), the primary KHI induces a vigorous but inherently transient burst of turbulence and associated irreversible mixing localised in the vicinity of the density interface, leading to a relatively well-mixed region bounded by stronger density gradients above and below. We explore the qualitatively different behaviour that arises when
$Re$), the primary KHI induces a vigorous but inherently transient burst of turbulence and associated irreversible mixing localised in the vicinity of the density interface, leading to a relatively well-mixed region bounded by stronger density gradients above and below. We explore the qualitatively different behaviour that arises when  $R\gg 1$, and so the density interface is sharp, with
$R\gg 1$, and so the density interface is sharp, with 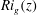 $Ri_{g}(z)$ now being maximum at the density interface
$Ri_{g}(z)$ now being maximum at the density interface 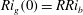 $Ri_{g}(0)=RRi_{b}$. This flow is primarily susceptible to Holmboe wave instability (HWI) (Holmboe, Geophys. Publ., vol. 24, 1962, pp. 67–113), which manifests at finite amplitude in this symmetric flow as counter-propagating trains of elliptical vortices above and below the density interface, thus perturbing the interface so as to exhibit characteristically cusped interfacial waves which thereby ‘scour’ the density interface. Unlike previous lower-
$Ri_{g}(0)=RRi_{b}$. This flow is primarily susceptible to Holmboe wave instability (HWI) (Holmboe, Geophys. Publ., vol. 24, 1962, pp. 67–113), which manifests at finite amplitude in this symmetric flow as counter-propagating trains of elliptical vortices above and below the density interface, thus perturbing the interface so as to exhibit characteristically cusped interfacial waves which thereby ‘scour’ the density interface. Unlike previous lower-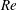 $Re$ experimental and numerical studies, when
$Re$ experimental and numerical studies, when 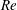 $Re$ is sufficiently high the primary HWI becomes increasingly more three-dimensional due to the emergence of shear-aligned secondary convective instabilities. As
$Re$ is sufficiently high the primary HWI becomes increasingly more three-dimensional due to the emergence of shear-aligned secondary convective instabilities. As  $Re$ increases, (i) the growth rate of secondary instabilities appears to saturate and (ii) the perturbation kinetic energy exhibits a
$Re$ increases, (i) the growth rate of secondary instabilities appears to saturate and (ii) the perturbation kinetic energy exhibits a 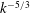 $k^{-5/3}$ spectrum for sufficiently large length scales that are influenced by anisotropic buoyancy effects. Therefore, at sufficiently high
$k^{-5/3}$ spectrum for sufficiently large length scales that are influenced by anisotropic buoyancy effects. Therefore, at sufficiently high 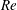 $Re$, vigorous turbulence is triggered that also significantly ‘scours’ the primary density interface, leading to substantial irreversible mixing and vertical transport of mass above and below the (robust) primary density interface. Furthermore, HWI produces a markedly more long-lived turbulence event compared to KHI at a similarly high
$Re$, vigorous turbulence is triggered that also significantly ‘scours’ the primary density interface, leading to substantial irreversible mixing and vertical transport of mass above and below the (robust) primary density interface. Furthermore, HWI produces a markedly more long-lived turbulence event compared to KHI at a similarly high 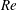 $Re$. Despite their vastly different mechanics (i.e. ‘overturning’ versus ‘scouring’) and localisation, the mixing induced by KHI and HWI is comparable in both absolute terms and relative efficiency. Our results establish that, provided the flow Reynolds number is sufficiently high, shear layers with sharp density interfaces and associated locally high values of the gradient Richardson number may still be sites of substantial and efficient irreversible mixing.
$Re$. Despite their vastly different mechanics (i.e. ‘overturning’ versus ‘scouring’) and localisation, the mixing induced by KHI and HWI is comparable in both absolute terms and relative efficiency. Our results establish that, provided the flow Reynolds number is sufficiently high, shear layers with sharp density interfaces and associated locally high values of the gradient Richardson number may still be sites of substantial and efficient irreversible mixing.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 61
- Cited by



