Published online by Cambridge University Press: 10 October 2016
Buoyancy effects on the turbulent mixing and entrainment processes were analysed in the case of a stratified plane shear layer between two horizontal air flows in conditions leading to relatively low values of the flux Richardson number (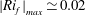 $|Ri_{f}|_{max}\simeq 0.02$). Velocity and temperature measurements were made with a single
$|Ri_{f}|_{max}\simeq 0.02$). Velocity and temperature measurements were made with a single  $\times$-wire probe thermo-anemometry technique, using multi-overheat sequences to deliver simultaneous velocity–temperature data at high frequency. The spatial resolution was found to be fine enough, in relation to the dissipative scale and the thermal diffusive scale, to avoid false mixing enhancement in the analysis of the physical mechanisms through velocity–temperature coupling in statistical turbulence quantities. Probability density functions (PDFs) and joint probability density functions (JPDFs) were used to distinguish between the different mechanisms involved in turbulent mixing, namely entrainment, engulfing, nibbling and mixing, and point to the contribution of entrainment in the mixing process. When comparing an unstably stratified configuration to its stably stratified equivalent, no significant difference could be seen in the PDF and JPDF quantities, but a conditional analysis based on temperature thresholding enabled a separation between mixed fluid and two distinct sets of events associated with unmixed fluid entrained from the hot and cold sides of the mixing layer into the mixing layer. This separation allowed a direct calculation of the entrainment velocities on both sides of the mixing layer. A significant increase of the total entrainment could be seen in the case of unstably stratified configuration. The entrainment ratios were compared to their prediction by the Dimotakis model and both a rather good relevance of the model and some need for improvement were found from the comparison. It was hypothesised that the improvement should come from better taking into account the distinct contributions of nibbling and engulfing inside the process of entrainment and mixing.
$\times$-wire probe thermo-anemometry technique, using multi-overheat sequences to deliver simultaneous velocity–temperature data at high frequency. The spatial resolution was found to be fine enough, in relation to the dissipative scale and the thermal diffusive scale, to avoid false mixing enhancement in the analysis of the physical mechanisms through velocity–temperature coupling in statistical turbulence quantities. Probability density functions (PDFs) and joint probability density functions (JPDFs) were used to distinguish between the different mechanisms involved in turbulent mixing, namely entrainment, engulfing, nibbling and mixing, and point to the contribution of entrainment in the mixing process. When comparing an unstably stratified configuration to its stably stratified equivalent, no significant difference could be seen in the PDF and JPDF quantities, but a conditional analysis based on temperature thresholding enabled a separation between mixed fluid and two distinct sets of events associated with unmixed fluid entrained from the hot and cold sides of the mixing layer into the mixing layer. This separation allowed a direct calculation of the entrainment velocities on both sides of the mixing layer. A significant increase of the total entrainment could be seen in the case of unstably stratified configuration. The entrainment ratios were compared to their prediction by the Dimotakis model and both a rather good relevance of the model and some need for improvement were found from the comparison. It was hypothesised that the improvement should come from better taking into account the distinct contributions of nibbling and engulfing inside the process of entrainment and mixing.