Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T03:52:26.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent kinetic energy production and flow structures in flows past smooth and rough walls

Published online by Cambridge University Press:  18 March 2019

P. Orlandi Open the ORCID record for P. Orlandi [Opens in a new window]
P. Orlandi*
Affiliation:
Dipartimento di Ingegneria Meccanica e Aerospaziale, Sapienza Università di Roma, Via Eudossiana 16, I-00184, Roma
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Data available in the literature from direct numerical simulations of two-dimensional turbulent channels by Lee & Moser (J. Fluid Mech., vol. 774, 2015, pp. 395–415), Bernardini et al. (J. Fluid Mech., 742, 2014, pp. 171–191), Yamamoto & Tsuji (Phys. Rev. Fluids, vol. 3, 2018, 012062) and Orlandi et al. (J. Fluid Mech., 770, 2015, pp. 424–441) in a large range of Reynolds number have been used to find that 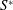$S^{\ast }$ the ratio between the eddy turnover time (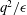$q^{2}/\unicode[STIX]{x1D716}$, with 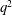$q^{2}$ being twice the turbulent kinetic energy and $\unicode[STIX]{x1D716}$ the isotropic rate of dissipation) and the time scale of the mean deformation (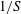$1/S$), scales very well with the Reynolds number in the wall region. The good scaling is due to the eddy turnover time, although the turbulent kinetic energy and the rate of isotropic dissipation show a Reynolds dependence near the wall; 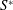$S^{\ast }$, as well as 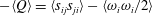$-\langle Q\rangle =\langle s_{ij}s_{ji}\rangle -\langle \unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D714}_{i}/2\rangle$ are linked to the flow structures, and also the latter quantity presents a good scaling near the wall. It has been found that the maximum of turbulent kinetic energy production 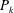$P_{k}$ occurs in the layer with 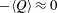$-\langle Q\rangle \approx 0$, that is, where the unstable sheet-like structures roll-up to become rods. The decomposition of 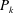$P_{k}$ in the contribution of elongational and compressive strain demonstrates that the two contributions present a good scaling. However, the good scaling holds when the wall and the outer structures are separated. The same statistics have been evaluated by direct simulations of turbulent flows in the presence of different types of corrugations on both walls. The flow physics in the layer near the plane of the crests is strongly linked to the shape of the surface and it has been demonstrated that the 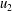$u_{2}$ (normal to the wall) fluctuations are responsible for the modification of the flow structures, for the increase of the resistance and of the turbulent kinetic energy production.

JFM classification

Turbulent Flows: Turbulence simulation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 897 - 928
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arenas, I., García, E., Orlandi, P., Fu, M. K., Hultmark, M. & Leonardi, S.2018 Comparison between super-hydrophobic, liquid infused and rough surfaces: a DNS study. arXiv:1812.05674 [physics.flu-dyn].Google Scholar
Aupoix, B. & Spalart, P. R. 2003 Extensions of the Spalart-Allmaras turbulence model to account for wall roughness. Intl J. Heat Fluid Flow 24, 454–462.Google Scholar
Bernardini, M., Pirozzoli, S. & Orland, P. 2014 Velocity statistics in turbulent channel flow up to Re 𝜏 = 4000. J. Fluid Mech. 742, 171–191.Google Scholar
Burattini, P., Leonardi, S., Orlandi, P. & Antonia, R. A. 2008 Comparison between experiments and direct numerical simulations in a channel flow with roughness on one wall. J. Fluid Mech. 600, 403–426.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Furuya, Y., Miyata, M. & Fujita, H. 1976 Turbulent boundary layer and flow resistance on plates roughened by wires. J. Fluids Engng 98, 635–644.Google Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.Google Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, 1–100.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611, 215–236.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near–wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Rundstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Lee, M. L., Kim, J. & Moin, P. 1990 Structure of turbulence at high shear rate. J. Fluid Mech. 216, 561–583.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct simulation of turbulent channel flow layer up to Re 𝜏 = 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lee, M. & Moser, R. D.2018 Spectral analysis of the budget equation in turbulent channel flows at high Re. arXiv:1806.01254v1 pp. 1–49.Google Scholar
Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L. & Antonia, A. R. 2003 Direct numerical simulations of turbulent channel flow with transverse square bars on the wall. J. Fluid Mech. 491, 229–238.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.Google Scholar
Moin, P. & Kim, J. 1997 Tackling turbulence with supercomputers. Sci. Am. 276, 62–68.Google Scholar
Nikuradse, J. 1950 Laws of flow in rough pipes. In NACA Technical Memorandum, vol. 1292.Google Scholar
Orlandi, P. 2000 Fluid Flow Phenomena – A Numerical Toolkit. Kluwer.Google Scholar
Orlandi, P. 2013 The importance of wall-normal Reynolds stress in turbulent rough channel flows. Phys. Fluids 25, 110813-12.Google Scholar
Orlandi, P., Bernardini, M. & Pirozzoli, S. 2015 Poiseuille and Couette flows in the transitional and fully turbulent regime. J. Fluid Mech. 770, 424–441.Google Scholar
Orlandi, P. & Leonardi, S. 2006 DNS of turbulent channel flows with two- and three-dimensional roughness. J. Turbul. 7, N53.Google Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2006 Turbulent channel with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.Google Scholar
Orlandi, P., Sassun, D. & Leonardi, S. 2016 DNS of conjugate heat transfer in presence of rough surfaces. Intl J. Heat Mass Transfer 100, 250–266.Google Scholar
Peskin, C. S. 1972 Flow patterns around heart valves: a numerical method. J. Comput. Phys. 25, 220–252.Google Scholar
Pirozzoli, S., Bernardini, M. & Grasso, F. 2010 On the dynamical relevance of coherent vortical structures in turbulent boundary layers. J. Fluid Mech. 648, 325–349.Google Scholar
Raupach, M. R., Finningan, J. J. & Brunet, Y. 1996 Coherent eddies and turbulence in vegetation canopies: the mixing layer analogy. Boundary-Layer Metereol. 78, 351–386.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flows, 2nd edn. Cambridge University Press.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence, 2nd edn. Springer.Google Scholar
Wallace, J. M. 2016 Quadrant analysis in turbulence research: history and evolution. Annu. Rev. Fluid Mech. 48, 131–158.Google Scholar
Yamamoto, Y. & Tsuji, Y. 2018 Numerical evidence of logarithmic regions in channel flow at Re 𝜏 = 8000. Phys. Rev. Fluids 3, 012062.Google Scholar