Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T13:58:57.923Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent horizontal convection under spatially periodic forcing: a regime governed by interior inertia

Published online by Cambridge University Press:  13 October 2017

Madelaine G. Rosevear Open the ORCID record for Madelaine G. Rosevear [Opens in a new window] ,
Bishakhdatta Gayen Open the ORCID record for Bishakhdatta Gayen [Opens in a new window]  and
Ross W. Griffiths Open the ORCID record for Ross W. Griffiths [Opens in a new window]
Madelaine G. Rosevear
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia
Bishakhdatta Gayen
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia
Ross W. Griffiths*
Affiliation:
Research School of Earth Sciences, Australian National University, Canberra, ACT 2601, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Differential heating applied at a single horizontal boundary forces ‘horizontal convection’, even when there is no net heat flux through the boundary. However, almost all studies of horizontal convection have been limited to a special class of problem in which temperature or heat flux differences were applied in only one direction and over the horizontal length of a box (the Rossby problem; Rossby, Deep-Sea Res., vol. 12, 1965, pp. 9–16). These conditions strongly constrain the flow. Here we report laboratory experiments and direct numerical simulations (DNS) extending the results of Griffiths & Gayen (Phys. Rev. Lett., vol. 115, 2015, 204301) for horizontal convection forced by boundary conditions imposed in a two-dimensional periodic array at a horizontal boundary. The experiments use saline and freshwater fluxes at a permeable base with the imposed boundary salinity having a horizontal length scale one quarter of the width of the box. The flow reaches a state in which the net boundary buoyancy flux vanishes and the bulk of the fluid shows an inertial range of turbulence length scales. A regime transition is seen for increasing water depth, from an array of individual coherent plumes on the forcing scale to convection dominated by emergent larger scales of overturning. The DNS explore the analogous thermally forced case with sinusoidal boundary temperature of wavenumber 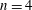$n=4$, and are used to examine the Rayleigh number (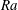$Ra$) dependence for shallow- and deep-water cases. For shallow water the flow transitions with increasing 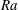$Ra$ from laminar to turbulent boundary layer regimes that are familiar from the Rossby problem and which have normalised heat transport scaling as 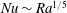$Nu\sim Ra^{1/5}$ and 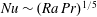$Nu\sim (Ra\,Pr)^{1/5}$, with 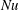$Nu$ the Nusselt number and 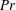$Pr$ the Prandtl number, in this case maintaining a stable array of coherent turbulent plumes. For deep-water and large 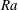$Ra$ the laminar scaling transitions to 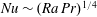$Nu\sim (Ra\,Pr)^{1/4}$, with the scales of turbulence extending to the dimensions of the box. The 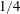$1/4$ power law regime is explained in terms of the momentum of symmetric, inviscid large scales of motion in the interior coupled to diffusive loss of heat through stabilised parts of the boundary layer. The turbulence production is predominantly by shear instability rather than convection, with viscous dissipation distributed throughout the bulk of the fluid. These conditions are not seen in the highly asymmetric flow in the Rossby problem even at Rayleigh numbers up to six orders of magnitude greater than the transition found here. The new inertial interior regime has the rate of supply of available potential energy, and its removal by mixing of density, increasing as 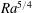$Ra^{5/4}$, which is faster than 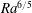$Ra^{6/5}$ in the Rossby problem. Irreversible mixing is confined close to the forcing boundary and is very much larger than the viscous dissipation, which is proportional to 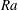$Ra$.

JFM classification

Convection: Convection Convection: Plumes/thermals Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 491 - 523
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.CrossRefGoogle Scholar
Barkan, R., Winters, K. & Llewellyn Smith, S. 2013 Rotating horizontal convection. J. Fluid Mech. 723, 556–586.CrossRefGoogle Scholar
Chiu-Webster, S., Hinch, E. J. & Lister, J. R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.Google Scholar
Gayen, B., Griffiths, R. W. & Hughes, G. O. 2014 Stability transitions and turbulence in horizontal convection. J. Fluid Mech. 751, 1–11.CrossRefGoogle Scholar
Gayen, B., Griffiths, R. W., Hughes, G. O. & Saenz, J. A. 2013a Energetics of horizontal convection. J. Fluid Mech. 716, R10.Google Scholar
Gayen, B., Hughes, G. O. & Griffiths, R. W. 2013b Completing the energy budget and pathways for Rayleigh–Bénard convection. Phys. Rev. Lett. 111, 124301.Google Scholar
Griffiths, R. W. & Gayen, B. 2015 Turbulent convection insights from small-scale thermal forcing with zero net heat flux at a horizontal boundary. Phys. Rev. Lett. 115, 204301.Google Scholar
Griffiths, R. W., Hughes, G. O. & Gayen, B. 2013 Horizontal convection dynamics: insights from transient adjustment. J. Fluid Mech. 726, 559–595.Google Scholar
Hignett, P., Ibbetson, A. & Killworth, P. D. 1981 On rotating thermal convection driven by non-uniform heating from below. J. Fluid Mech. 109, 161–187.Google Scholar
Hughes, G. O., Gayen, B. & Griffiths, R. W. 2013 Available potential energy in Rayleigh–Bénard convection. J. Fluid Mech. 729, R3.CrossRefGoogle Scholar
Hughes, G. O. & Griffiths, R. W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40, 185–208.Google Scholar
Hughes, G. O., Griffiths, R. W., Mullarney, J. C. & Peterson, W. H. 2007 A theoretical model for horizontal convection at high Rayleigh number. J. Fluid Mech. 581, 251–276.Google Scholar
Hughes, G. O., Hogg, A. M. & Griffiths, R. W. 2009 Available potential energy and irreversible mixing in the meridional overturning circulation. J. Phys. Oceanogr. 39, 3130–3146.CrossRefGoogle Scholar
Mullarney, J. C., Griffiths, R. W. & Hughes, G. O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.Google Scholar
Nokes, R.2014 Streams, version 2.03: system theory and design. Tech. Rep. Department of Civil and Natural Resources Engineering, University of Canterbury, New Zealand.Google Scholar
Paparella, F. & Young, W. R. 2002 Horizontal convection is non-turbulent. J. Fluid Mech. 466, 205–214.Google Scholar
Park, Y. G. & Whitehead, J. A. 1999 Rotating convection driven by differential bottom heating. J. Phys. Oceanogr. 29, 1208–1220.2.0.CO;2>CrossRefGoogle Scholar
Pierce, D. W. & Rhines, P. B. 1996 Convective building of a pycnocline: laboratory experiments. J. Phys. Oceanogr. 26, 176–190.Google Scholar
Rossby, H. T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep-Sea Res. 12, 9–16.Google Scholar
Rossby, H. T. 1998 Numerical experiments with a fluid non-uniformly heated from below. Tellus 50, 242–257.Google Scholar
Saenz, J. A., Hogg, A. M., Hughes, G. O. & Griffiths, R. W. 2012 Mechanical power input from buoyancy and wind to the circulation in an ocean model. Geophys. Res. Lett. 39, L13605.Google Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really ‘non-turbulent’? Geophys. Res. Lett. 38, L21609.Google Scholar
Sheard, G. J., Hussama, W. K. & Tsai, T. 2016 Linear stability and energetics of rotating radial horizontal convection. J. Fluid Mech. 795, 1–35.CrossRefGoogle Scholar
Sheard, G. J. & King, M. P. 2011 Horizontal convection: effect of aspect ratio on Rayleigh number scaling and stability. Appl. Math. Model. 35, 1647–1655.Google Scholar
Shishkina, O., Grossmann, S. & Lohse, D. 2016 Prandtl number dependence of heat transport in horizontal convection. Geophys. Res. Lett. 116, 024302.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010 Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid Mech. 643, 495–507.CrossRefGoogle Scholar
Stewart, K. D., Hughes, G. O. & Griffiths, R. W. 2012 The role of turbulent mixing in an overturning circulation maintained by surface buoyancy forcing. J. Phys. Oceanogr. 42, 1907–1922.Google Scholar
Stommel, H. 1962 On the smallness of sinking regions in the ocean. Proc. Natl Acad. Sci. USA 48, 766–772.Google Scholar
Tailleux, R. 2009 On the energetics of stratified turbulent mixing, irreversible thermodynamics, Boussinesq models and the ocean heat engine controversy. J. Fluid Mech. 638, 339–382.Google Scholar
Vreugdenhil, C., Gayen, B. & Griffiths, R. W. 2016 Mixing and dissipation in a geostrophic buoyancy-driven circulation. J. Geophys. Res. Oceans 121, 6076–6091.CrossRefGoogle Scholar
Vreugdenhil, C., Griffiths, R. W. & Gayen, B. 2017 Geostrophic and chimney regimes in rotating horizontal convection with imposed heat flux. J. Fluid Mech. 823, 57–99.Google Scholar
Whitehead, J. A. & Wang, W. 2008 A laboratory model of vertical ocean circulation driven by mixing. J. Phys. Oceanogr. 38, 1091–1106.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Winton, M. 1995 Why is the deep sinking narrow? J. Phys. Oceanogr. 25, 997–1005.2.0.CO;2>CrossRefGoogle Scholar