Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Song, Jiaxing
Teng, Hao
Liu, Nansheng
Ding, Hang
Lu, Xi-Yun
and
Khomami, Bamin
2019.
The correspondence between drag enhancement and vortical structures in turbulent Taylor–Couette flows with polymer additives: a study of curvature dependence.
Journal of Fluid Mechanics,
Vol. 881,
Issue. ,
p.
602.
Jiménez, Javier
2020.
Computers and turbulence.
European Journal of Mechanics - B/Fluids,
Vol. 79,
Issue. ,
p.
1.
Li, Qingxiang
Pan, Ming
Zhou, Quan
and
Dong, Yuhong
2020.
Turbulent drag modification in open channel flow over an anisotropic porous wall.
Physics of Fluids,
Vol. 32,
Issue. 1,
Zhu, Yabiao
Song, Jiaxing
Liu, Nansheng
Lu, Xiyun
and
Khomami, Bamin
2020.
Polymer-induced flow relaminarization and drag enhancement in spanwise-rotating plane Couette flow.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Mohammadtabar, M.
Sanders, R.S.
and
Ghaemi, S.
2020.
Viscoelastic properties of flexible and rigid polymers for turbulent drag reduction.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 283,
Issue. ,
p.
104347.
Marchioli, Cristian
and
Campolo, Marina
2021.
Drag Reduction in Turbulent Flows by Polymer and Fiber Additives.
KONA Powder and Particle Journal,
Vol. 38,
Issue. 0,
p.
64.
Shaqfeh, Eric S.G.
and
Khomami, Bamin
2021.
The Oldroyd-B fluid in elastic instabilities, turbulence and particle suspensions.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 298,
Issue. ,
p.
104672.
Song, Jiaxing
Lin, Fenghui
Liu, Nansheng
Lu, Xi-Yun
and
Khomami, Bamin
2021.
Direct numerical simulation of inertio-elastic turbulent Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 926,
Issue. ,
Mortimer, L. F.
and
Fairweather, M.
2022.
Prediction of polymer extension, drag reduction, and vortex interaction in direct numerical simulation of turbulent channel flows.
Physics of Fluids,
Vol. 34,
Issue. 7,
Pakzad, Hossein
Nouri-Borujerdi, Ali
and
Moosavi, Ali
2022.
Drag reduction ability of slippery liquid-infused surfaces: A review.
Progress in Organic Coatings,
Vol. 170,
Issue. ,
p.
106970.
Zhu, Yabiao
Song, Jiaxing
Lin, Fenghui
Liu, Nansheng
Lu, Xiyun
and
Khomami, Bamin
2022.
Relaminarization of spanwise-rotating viscoelastic plane Couette flow via a transition sequence from a drag-reduced inertial to a drag-enhanced elasto-inertial turbulent flow.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Javanappa, Shashi Kumar
and
Narasimhamurthy, Vagesh D.
2022.
Structure of turbulence in planar rough Couette flows.
Physics of Fluids,
Vol. 34,
Issue. 6,
Lin, Che-Yu
Owolabi, Bayode E.
and
Lin, Chao-An
2022.
Polymer-turbulence interactions in a complex flow and implications for the drag reduction phenomenon.
Physics of Fluids,
Vol. 34,
Issue. 4,
Brethouwer, Geert
2023.
Strong dissimilarity between heat and momentum transfer in rotating Couette flows.
International Journal of Heat and Mass Transfer,
Vol. 205,
Issue. ,
p.
123920.
He, Xixing
Liu, Yihe
Zhan, Haiyang
Liu, Yahua
Zhao, Lei
and
Feng, Shile
2023.
Bidirectional Underwater Drag Reduction on Bionic Flounder Two-Tier Structural Surfaces.
Biomimetics,
Vol. 8,
Issue. 1,
p.
116.
2023.
Rotation effects on turbulence features of viscoelastic spanwise-rotating plane Couette flows.
Physics of Fluids,
Vol. 35,
Issue. 6,
Lin, Fenghui
Song, Jiaxing
Zhao, Zhiye
Liu, Nansheng
Lu, Xi-Yun
and
Khomami, Bamin
2023.
A novel transition route to elastically dominated turbulence in viscoelastic Taylor–Couette flow.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 312,
Issue. ,
p.
104968.
Song, Jiaxing
Zhu, Yabiao
Lin, Fenghui
Liu, Nansheng
and
Khomami, Bamin
2023.
Turbulent Taylor–Couette flow of dilute polymeric solutions: a 10-year retrospective.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2243,
Zhu, Yabiao
Wan, Zhenhua
Lin, Fenghui
Liu, Nansheng
Lu, Xiyun
and
Khomami, Bamin
2023.
Maximum drag enhancement asymptote in spanwise-rotating viscoelastic plane Couette flow of dilute polymeric solutions.
Journal of Fluid Mechanics,
Vol. 958,
Issue. ,
Rahimi, Amirmohammad
Shahsavari, Arghavan
Pakzad, Hossein
Moosavi, Ali
and
Nouri-Borujerdi, Ali
2023.
Laminar drag reduction ability of liquid-infused microchannels by considering different infused lubricants.
The Journal of Chemical Physics,
Vol. 158,
Issue. 7,
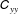 $\unicode[STIX]{x1D60A}_{yy}$
and
$\unicode[STIX]{x1D60A}_{yy}$
and
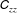 $\unicode[STIX]{x1D60A}_{zz}$
in this region. This finding is in stark contrast to that of drag-reduced PPF where the polymer stretch and the exchanges between elastic potential energy and turbulent kinetic energy in the core region are insignificant; to this end, in drag-reduced PPF, peak values of the conformation tensor components appear in the near-wall region. Therefore, this study paves the way for understanding the underlying flow physics in drag-reduced PCF, particularly in the context of elastic theory. Moreover, the longitudinal large-scale streaks at the channel centre of drag-reduced PCF are greatly strengthened due to the increased production/dissipation ratio; the LSS imprint effects on the near-wall flow of drag-reduced PCF monotonically increase as the Weissenberg number is enhanced.
$\unicode[STIX]{x1D60A}_{zz}$
in this region. This finding is in stark contrast to that of drag-reduced PPF where the polymer stretch and the exchanges between elastic potential energy and turbulent kinetic energy in the core region are insignificant; to this end, in drag-reduced PPF, peak values of the conformation tensor components appear in the near-wall region. Therefore, this study paves the way for understanding the underlying flow physics in drag-reduced PCF, particularly in the context of elastic theory. Moreover, the longitudinal large-scale streaks at the channel centre of drag-reduced PCF are greatly strengthened due to the increased production/dissipation ratio; the LSS imprint effects on the near-wall flow of drag-reduced PCF monotonically increase as the Weissenberg number is enhanced.


