Article contents
Turbulent channel flow of suspensions of neutrally buoyant particles over porous media
Published online by Cambridge University Press: 29 December 2022
Abstract
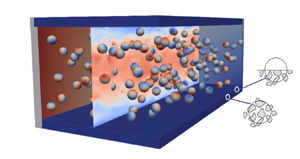
This study discusses turbulent suspension flows of non-Brownian, non-colloidal, neutrally buoyant and rigid spherical particles in a Newtonian fluid over porous media with particles too large to penetrate and move through the porous layer. We consider suspension flows with the solid volume fraction  ${{\varPhi _b}}$ ranging from 0 to 0.2, and different wall permeabilities, while porosity is constant at 0.6. Direct numerical simulations with an immersed boundary method are employed to resolve the particles and flow phase, with the volume-averaged Navier–Stokes equations modelling the flow within the porous layer. The results show that in the presence of particles in the free-flow region, the mean velocity and the concentration profiles are altered with increasing porous layer permeability because of the variations in the slip velocity and wall-normal fluctuations at the suspension-porous interface. Furthermore, we show that variations in the stress condition at the interface significantly affect the particle near-wall dynamics and migration toward the channel core, thereby inducing large modulations of the overall flow drag. At the highest volume fraction investigated here,
${{\varPhi _b}}$ ranging from 0 to 0.2, and different wall permeabilities, while porosity is constant at 0.6. Direct numerical simulations with an immersed boundary method are employed to resolve the particles and flow phase, with the volume-averaged Navier–Stokes equations modelling the flow within the porous layer. The results show that in the presence of particles in the free-flow region, the mean velocity and the concentration profiles are altered with increasing porous layer permeability because of the variations in the slip velocity and wall-normal fluctuations at the suspension-porous interface. Furthermore, we show that variations in the stress condition at the interface significantly affect the particle near-wall dynamics and migration toward the channel core, thereby inducing large modulations of the overall flow drag. At the highest volume fraction investigated here,  ${{\varPhi _b}}= 0.2$, the velocity fluctuations and the Reynolds shear stress are found to decrease, and the overall drag increases due to the increase in the particle-induced stresses.
${{\varPhi _b}}= 0.2$, the velocity fluctuations and the Reynolds shear stress are found to decrease, and the overall drag increases due to the increase in the particle-induced stresses.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by



