Published online by Cambridge University Press: 03 April 2020
The equations governing the mean fluid motions within a turbulent boundary layer adjoining a stationary plane beneath an axisymmetric circumferential flow  $v_{\infty }(r)$, where
$v_{\infty }(r)$, where  $r$ is cylindrical radius, are solved by assuming the eddy diffusivity is proportional to
$r$ is cylindrical radius, are solved by assuming the eddy diffusivity is proportional to  $v_{\infty }$ times a diffusivity function
$v_{\infty }$ times a diffusivity function  $L(r,z)$, where
$L(r,z)$, where  $z$ is axial distance from the plane. The boundary-layer shape and structure depend on the dimensionless vorticity
$z$ is axial distance from the plane. The boundary-layer shape and structure depend on the dimensionless vorticity  $\unicode[STIX]{x1D703}=\text{d}(rv_{\infty })/2v_{\infty }\,\text{d}r$, but are independent of the strength of the circumferential flow. This problem has been solved using a spectral method in the case of rigid-body motion (
$\unicode[STIX]{x1D703}=\text{d}(rv_{\infty })/2v_{\infty }\,\text{d}r$, but are independent of the strength of the circumferential flow. This problem has been solved using a spectral method in the case of rigid-body motion ( $\unicode[STIX]{x1D703}=1$ and
$\unicode[STIX]{x1D703}=1$ and  $v_{\infty }\sim r$) for two models of
$v_{\infty }\sim r$) for two models of  $L$:
$L$:  $L$ constant (model A) and
$L$ constant (model A) and  $L$ constant within a rough layer of thickness
$L$ constant within a rough layer of thickness  $z_{0}$ adjoining the boundary and increasing linearly with
$z_{0}$ adjoining the boundary and increasing linearly with  $z$ outside that layer (model B). The influence of the rough layer is quantified by the dimensionless radial coordinate
$z$ outside that layer (model B). The influence of the rough layer is quantified by the dimensionless radial coordinate  $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D716}r/z_{0}$, where
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D716}r/z_{0}$, where  $\unicode[STIX]{x1D716}\ll 1$. The boundary-layer thickness varies parabolically with
$\unicode[STIX]{x1D716}\ll 1$. The boundary-layer thickness varies parabolically with  $r$ for model A and nearly linearly with
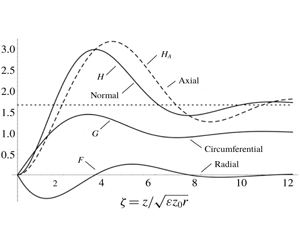
$r$ for model A and nearly linearly with  $r$ for model B. Inertial stability of the outer flow causes the velocity components to decay with axial distance as exponentially damped oscillations, with the radial flow consisting of a sequence of jets. Axial flow is positive (flowing out of the boundary layer). Outflow from the layer, velocity gradients at the bounding plane, meridional-plane circulation and oscillations all increase as radius decreases.
$r$ for model B. Inertial stability of the outer flow causes the velocity components to decay with axial distance as exponentially damped oscillations, with the radial flow consisting of a sequence of jets. Axial flow is positive (flowing out of the boundary layer). Outflow from the layer, velocity gradients at the bounding plane, meridional-plane circulation and oscillations all increase as radius decreases.