Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-01-25T06:06:03.121Z Has data issue: false hasContentIssue false
  • English
  • Français

Transition to bluff-body dynamics in the wake of vertical-axis wind turbines

Published online by Cambridge University Press:  19 January 2017

Daniel B. Araya ,
Tim Colonius  and
John O. Dabiri
Daniel B. Araya*
Affiliation:
Department of Mechanical Engineering, University of Houston, Houston, TX 77204, USA
Tim Colonius
Affiliation:
Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA 91125, USA
John O. Dabiri
Affiliation:
Department of Mechanical Engineering and Department of Civil and Environmental Engineering, Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

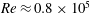We present experimental data to demonstrate that the far wake of a vertical-axis wind turbine (VAWT) exhibits features that are quantitatively similar to that of a circular cylinder with the same aspect ratio. For a fixed Reynolds number ($Re\approx 0.8\times 10^{5}$) and variable tip-speed ratio, two-dimensional particle image velocimetry (PIV) is used to measure the velocity field in the wake of four different laboratory-scale models: a 2-bladed, 3-bladed and 5-bladed VAWT, as well as a circular cylinder. With these measurements, we use spectral analysis and proper orthogonal decomposition (POD) to evaluate statistics of the velocity field and investigate the large-scale coherent motions of the wake. In all cases, we observe three distinct regions in the VAWT wake: (i) the near wake, where periodic blade vortex shedding dominates; (ii) a transition region, where growth of a shear-layer instability occurs; (iii) the far wake, where bluff-body wake oscillations dominate. We define a dynamic solidity parameter, 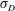$\unicode[STIX]{x1D70E}_{D}$, that relates the characteristic scales of the flow to the streamwise transition location in the wake. In general, we find that increasing 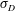$\unicode[STIX]{x1D70E}_{D}$ leads to an earlier transition, a greater initial velocity deficit and a faster rate of recovery in the wake. We propose a coordinate transformation using 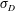$\unicode[STIX]{x1D70E}_{D}$ in which the minimum velocity recovery profiles of the VAWT wake closely match that of the cylinder wake. The results have implications for manipulating VAWT wake recovery within a wind farm.

JFM classification

Turbulent Flows: Turbulent Flows Vortex Flows: Vortex Flows Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 813 , 25 February 2017 , pp. 346 - 381
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, S. J., Sørensen, J. N. & Mikkelsen, R. 2013 Simulation of the inherent turbulence and wake interaction inside an infinitely long row of wind turbines. J. Turbul. 14, 1–24.Google Scholar
Araya, D. B. & Dabiri, J. O. 2015 A comparison of wake measurements in motor-driven and flow-driven turbine experiments. Exp. Fluids 56 (7), 1–15.Google Scholar
Bachant, P. & Wosnik, M. 2015 Characterising the near-wake of a cross-flow turbine. J. Turbul. 16 (4), 392–410.Google Scholar
Battisti, L., Zanne, L., Anna, S. D., Dossena, V., Persico, G. & Paradiso, B. 2011 Aerodynamic measurements on a vertical axis wind turbine in a large scale wind tunnel. J. Energ. Resour. 133, 031201.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Buhl, M. L.2005 A new empirical relationship between thrust coefficient and induction factor for the turbulent windmill state. Tech. Rep. NREL/TP-500-36834. National Renewable Energy Laboratory.CrossRefGoogle Scholar
Calaf, M., Meneveau, C. & Meyers, J. 2010 Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 22, 015110.CrossRefGoogle Scholar
Chamorro, L. P., Hill, C., Morton, S., Ellis, C., Arndt, R. E. A. & Sotiropoulos, F. 2013 On the interaction between a turbulent open channel flow and an axial-flow turbine. J. Fluid Mech. 716, 658–670.Google Scholar
Dabiri, J. O. 2014 Emergent aerodynamics in wind farms. Phys. Today 67, 66–67.Google Scholar
Dunne, R. & McKeon, B. J. 2015 Dynamic stall on a pitching and surging airfoil. Exp. Fluids 56 (8), 1–15.Google Scholar
Edwards, J. M., Danao, L. A. & Howell, R. J. 2015 PIV measurements and CFD simulation of the performance and flow physics and of a small-scale vertical axis wind turbine. Wind Energy 18, 201–217.Google Scholar
Eggleston, D. & Stoddard, F. 1987 Wind Turbine Engineering Design. Van Nostrand Reinhold Co. Inc.Google Scholar
Feng, L.-H., Wang, J.-J. & Pan, C. 2011 Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control. Phys. Fluids 23, 014106.Google Scholar
Ferreira, C. S., van Kuik, G., van Bussel, G. & Scarano, F. 2009 Visualization by PIV of dynamic stall on a vertical axis wind turbine. Exp. Fluids 46, 97–108.Google Scholar
Fujisawa, N. & Shibuya, S. 2001 Observations of dynamic stall on Darrieus wind turbine blades. J. Wind Engng Ind. Aerodyn. 89, 201–214.Google Scholar
Hamilton, N., Tutkun, M. & Cal, R. B. 2015 Wind turbine boundary layer arrays for Cartesian and staggered configurations: part II, low-dimensional representations via the proper orthogonal decomposition. Wind Energy 18, 297–315.Google Scholar
Hansen, M. O. L. 2008 Aerodynamics of Wind Turbines, 2nd edn. Earthscan.Google Scholar
Hansen, M. O. L., Sørensen, J. N., Voutsinas, S., Sørensen, N. & Madsen, H. A. 2006 State of the art in wind turbine aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 42, 285–330.Google Scholar
Hau, E. 2005 Wind Turbines, 2nd edn. Springer.Google Scholar
Högström, U. D., Asimakopoulos, D. N., Kambezidis, H., Helmist, C. G. & Smedman, A. 1988 A field study of the wake behind a 2MW wind turbine. Atmos. Environ. 22, 803–820.Google Scholar
Iungo, G. V. & Porté-Agel, Fernando 2014 Volumetric lidar scanning of wind turbine wakes under convective and neutral atmospheric stability regimes. J. Atmos. Ocean. Technol. 31, 2035–2048.Google Scholar
Iungo, G. V., Viola, F., Camarri, S., Porté-Agel, F. & Gallaire, F. 2013 Linear stability analysis of wind turbine wakes performed on wind tunnel measurements. J. Fluid Mech. 737, 499–526.CrossRefGoogle Scholar
Kinzel, M., Mulligan, Q. & Dabiri, J. O. 2012 Energy exchange in an array of vertical-axis wind turbines. J. Turbul. 13 (38), 1–13.Google Scholar
Kostas, J., Soria, J. & Chong, M. S. 2005 A comparison between snapshot POD analysis of PIV velocity and vorticity data. Exp. Fluids 38, 146–160.CrossRefGoogle Scholar
Lam, K. M. 2009 Vortex shedding flow behind a slowly rotating circular cylinder. J. Fluids Struct. 25, 245–262.Google Scholar
Laneville, A. & Vittecoq, P. 1986 Dynamic stall: the case of the vertical axis wind turbine. J. Solar Energy Engng 108, 140–145.CrossRefGoogle Scholar
Larsen, G. C., Madsen, H. A., Thomsen, K. & Larsen, T. J. 2008 Wake meandering: a pragmatic approach. Wind Energy 11, 377–395.Google Scholar
Leishman, G. J. 2006 Principles of Helicopter Aerodynamics. Cambridge University Press.Google Scholar
Madsen, H. A.1982 The actuator cylinder – a flow model for vertical axis wind turbines. PhD thesis, Aalborg University Center.Google Scholar
Medici, D. & Alfredsson, P. H. 2006 Measurements on a wind turbine wake: 3D effects and bluff body vortex shedding. Wind Energy 9, 219–236.Google Scholar
Medici, D. & Alfredsson, P. H. 2008 Measurements behind model wind turbines: further evidence of wake meandering. Wind Energy 11, 211–217.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.CrossRefGoogle Scholar
Myers, L. E. & Bahaj, A. S. 2010 Experimental analysis of the flow field around horizontal axis tidal turbines by use of scale mesh disk rotor simulators. Ocean Engng 37, 218–227.CrossRefGoogle Scholar
Okulov, V. L., Naumov, I. V., Mikkelsen, R. F., Kabardin, I. K. & Sørensen, J. N. 2014 A regular strouhal number for large-scale instability in the far wake of a rotor. J. Fluid Mech. 747, 369–380.Google Scholar
Picard, C. & Delville, J. 2000 Pressure velocity coupling in a subsonic round jet. Intl J. Heat Fluid Flow 21, 359–364.Google Scholar
Porté-Agel, F., Wu, Y.-T. & Chen, C.-H. 2013 A numerical study of the effects of wind direction on turbine wakes and power losses in a large wind farm. Energy 6, 5297–5313.Google Scholar
Rolin, V. & Porté-Agel, F. 2015 Wind-tunnel study of the wake behind a vertical axis wind turbine in a boundary layer flow using stereoscopic particle image velocimetry. J. Phys.: Conf. Ser. 625, 012012.Google Scholar
Roshko, A. 1961 Experiments on the flow past a circular cylinder at very high Reynolds number. J. Fluid Mech. 10, 345–356.Google Scholar
Schlichting, H. 1960 Boundary Layer Theory, 4th edn. McGraw-Hill.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures part I: coherent structures. Q. Appl. Maths XLV, 561–571.Google Scholar
Sutherland, H. J., Berg, D. E. & Ashwill, T. D.2012 A restrospective of VAWT technology Tech. Rep. SAND2012-0304. Sandia National Laboratories.Google Scholar
Tescione, G., Ragni, D., He, C., Ferreira, C. J., Simão & van Bussel, G. J. W. 2014 Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. J. Renew. Energ. 70, 47–61.Google Scholar
Thomsen, K. & Sørensen, P. 1999 Fatigue loads for wind turbines operating in wakes. J. Wind Engng Ind. Aerodyn. 80, 121–136.Google Scholar
VerHulst, C. & Meneveau, C. 2014 Large eddy simulation study of the kinetic energy entrainment by energetic turbulent flow structures in large wind farms. Phys. Fluids 26, 025113.Google Scholar
Vermeer, L. J., Sørensen, J. N. & Crespo, A. 2003 Wind turbine wake aerodynamics. Prog. Aerosp. Sci. 39, 467–510.Google Scholar
Welch, P. D. 1967 The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73.Google Scholar
Zhang, W., Markfort, C. D. & Porté-Agel, F. 2013 Wind turbine wakes in a convective boundary layer: a wind tunnel-study. Boundary-Layer Meteorol. 146, 161–179.Google Scholar