Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-09T06:27:25.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient electrohydrodynamics of a liquid drop at finite Reynolds numbers

Published online by Cambridge University Press:  27 April 2020

Asghar Esmaeeli Open the ORCID record for Asghar Esmaeeli [Opens in a new window]  and
Ali Behjatian
Asghar Esmaeeli*
Affiliation:
Southern Illinois University Carbondale, Carbondale, IL62901, USA
Ali Behjatian
Affiliation:
Southern Illinois University Carbondale, Carbondale, IL62901, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

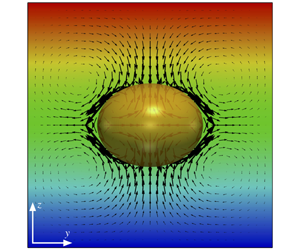
Transient electrohydrodynamics of a liquid drop at finite Reynolds numbers is studied by computer simulations. The governing equations of the problem are solved using a parallelized front tracking/finite difference method in the framework of the Taylor–Melcher leaky dielectric theory. The effect of the dielectric properties of the fluids on the dynamic response of the drop is studied by considering three representative fluid systems, which encompass all the regions of the deformation–circulation map. A parametric study is performed over a range of capillary number $Ca$, the Ohnesorge number squared $Oh^{2}$ and the viscosity ratio $\widetilde{\unicode[STIX]{x1D707}}$ to explore the effect of these parameters on the dynamic response. At low to intermediate capillary numbers, the dynamic response resembles that of a first- or second-order mechanical system, where the deformation settles to a steady state monotonically or through oscillations. However, beyond a threshold capillary number, the dynamic response becomes nonlinear. It is shown that the Ohnesorge number squared $Oh^{2}$ and the viscosity ratio $\widetilde{\unicode[STIX]{x1D707}}$ are the key parameters that determine the transition from a monotonic response to an oscillatory one (and vice versa) in density-matched fluid systems. To predict the dynamic response of nearly spherical drops at arbitrary $Oh^{2}$, an analytical equation is developed, which results in a critical Ohnesorge number squared $Oh_{c}^{2}$ that demarks a monotonic response from an oscillatory one. Investigations on the effect of the viscosity ratio $\widetilde{\unicode[STIX]{x1D707}}$ on the dynamic response shows that the relaxation time (for monotonic response) increases with an increase in $\widetilde{\unicode[STIX]{x1D707}}$ and that the steady state deformation ${\mathcal{D}}_{ss}$ correlates positively with $\widetilde{\unicode[STIX]{x1D707}}$ for oblate drops; however, depending on the corresponding regions of prolate drops on the deformation–circulation map, ${\mathcal{D}}_{ss}$ correlates positively or negatively with $\widetilde{\unicode[STIX]{x1D707}}$. A long-standing misconception regarding the oblate region is also rectified by development of a normal stress map, which determines the relative importance of the electric pressure and the normal hydrodynamic stress in setting the sense of the deformation of the drop.

JFM classification

Drops and Bubbles: Electrohydrodynamic effects Drops and Bubbles: Drops
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , A26
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajayi, O. O. 1978 A note on Taylor’s electrohydrodynamic theory. Proc. R. Soc. Lond. A 364 (1719), 499–507.Google Scholar
Allan, R. S. & Mason, S. G. 1962 Particle behavior in shear and electric fields. I. Deformation and burst of fluid drops. Proc. R. Soc. Lond. A 267, 45–61.Google Scholar
Basaran, O. A., Scott, T. C. & Byers, C. H. 1989 Drop oscillations in liquid–liquid systems. AIChE J. 35 (8), 1263–1270.CrossRefGoogle Scholar
Bentenitis, N. & Krause, S. 2005 Droplet deformation in DC electric fields: the extended leaky dielectric model. Langmuir 21 (14), 6194–6209.CrossRefGoogle Scholar
Castellanos, A. & Gonzalez, A. 1998 Nonlinear electrohydrodynamics of free surfaces. IEEE Trans. Dielec. Elec. Insul. 5 (3), 334–343.CrossRefGoogle Scholar
Das, D. & Saintillan, D. 2017a Electrohydrodynamics of viscous drops in strong electric fields: numerical simulations. J. Fluid Mech. 829, 127–152.CrossRefGoogle Scholar
Das, D. & Saintillan, D. 2017b A nonlinear small-deformation theory for transient droplet electrohydrodynamics. J. Fluid Mech. 810, 225–253.CrossRefGoogle Scholar
Dubash, N. & Mestel, A. J. 2007a Behaviour of a conducting drop in a highly viscous fluid subject to an electric field. J. Fluid Mech. 581, 469–493.CrossRefGoogle Scholar
Dubash, N. & Mestel, A. J. 2007b Breakup behavior of a conducting drop suspended in a viscous fluid subject to an electric field. Phys. Fluids 19, 072101.Google Scholar
Esmaeeli, A. 2016 Dielectrophoretic- and electrohydrodynamic-driven translational motion of a liquid column in transverse electric fields. Phys. Fluids 28 (7), 073306.CrossRefGoogle Scholar
Esmaeeli, A. & Behjatian, A. 2012 Electrohydrodynamics of a liquid drop in confined domains. Phys. Rev. E 86 (3), 036310.Google ScholarPubMed
Esmaeeli, A. & Sharifi, P. 2011 Transient electrohydrodynamics of a liquid drop. Phys. Rev. E 84, 036308.Google ScholarPubMed
Esmaeeli, A. & Tryggvason, G. 2005 A direct numerical simulation study of the buoyant rise of bubbles at O (100) Reynolds number. Phys. Fluids 17 (9), 093303.CrossRefGoogle Scholar
Feng, J. Q. 1999 Electrohydrodynamic behaviour of a drop subjected to a steady uniform electric field at finite electric Reynolds number. Proc. R. Soc. Lond. A 455 (1986), 2245–2269.CrossRefGoogle Scholar
Feng, J. Q. & Scott, T. C. 1996 A computational analysis of electrohydrodynamics of a leaky dielectric drop in an electric field. J. Fluid Mech. 311, 289–326.CrossRefGoogle Scholar
Garton, C. G. & Krasucki, Z. 1964 Bubbles in insulating liquids: stability in an electric field. Proc. R. Soc. Lond. A 280, 211–216.Google Scholar
Ha, J.-W. & Yang, S.-M. 1995 Effects of surfactant on the deformation and stability of a drop in a viscous fluid in an electric field. J. Colloid Interface Sci. 175, 369–385.CrossRefGoogle Scholar
Ha, J.-W. & Yang, S.-M. 2000 Deformation and breakup of Newtonian and non-Newtonian conducting drops in an electric field. J. Fluid Mech. 405, 131–156.CrossRefGoogle Scholar
Halim, M. A. & Esmaeeli, A. 2013 Computational studies on the transient electrohydrodynamics of a liquid drop. FDMP: Fluid Dyn. Mater. Proc. 9 (4), 435–460.Google Scholar
Haywood, R. J., Renksizbulut, M. & Raithby, G. D. 1991 Transient deformation of freely-suspended liquid droplets in electrostatic fields. AIChE J. 37 (9), 1305–1317.CrossRefGoogle Scholar
Lac, E. & Homsy, G. M. 2007 Axisymmetric deformation and stability of a viscous drop in a steady electric field. J. Fluid Mech. 590, 239–264.CrossRefGoogle Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2013 The influence of inertia and charge relaxation on electrohydrodynamic drop deformation. Phys. Fluids 25 (11), 112101.CrossRefGoogle Scholar
Lanauze, J. A., Walker, L. M. & Khair, A. S. 2015 Nonlinear electrohydrodynamics of slightly deformed oblate drops. J. Fluid Mech. 774, 245–266.CrossRefGoogle Scholar
Macky, W. A. 1931 Some investigations on the deformation and breaking of water drops in strong electric fields. Proc. R. Soc. Lond. A 133, 565–587.Google Scholar
Mandal, S., Chaudhury, K. & Chakraborty, S. 2014 Transient dynamics of confined liquid drops in a uniform electric field. Phys. Rev. E 89 (5), 053020.Google Scholar
Marston, P. L. 1980 Shape oscillation and static deformation of drops and bubbles driven by modulated radiation stressestheory. J. Acoust. Soc. Am. 67 (1), 15–26.CrossRefGoogle Scholar
Melcher, J. R. & Schwarz, W. J. 1968 Interfacial relaxation overstability in a tangential electric field. Phys. Fluids 11 (12), 2604–2616.CrossRefGoogle Scholar
Melcher, J. R. & Smith, C. V. 1969 Electrohydrodynamic charge relaxation and interfacial perpendicular-field instability. Phys. Fluids 12 (4), 778–790.CrossRefGoogle Scholar
Melcher, J. R. & Taylor, G. I. 1969 Electrohydrodynamics: a review of the role of interfacial shear stresses. Annu. Rev. Fluid Mech. 1, 111–147.CrossRefGoogle Scholar
Miller, C. A. & Scriven, L. E. 1968 The oscillations of a fluid droplet immersed in another fluid. J. Fluid Mech. 32 (3), 417–435.CrossRefGoogle Scholar
Moriya, S., Adachi, K. & Kotaka, T. 1986 Deformation of droplets suspended in viscous media in an electric field. 1. Rate of deformation. Langmuir 2 (2), 155–160.CrossRefGoogle Scholar
Nishiwaki, T., Adachi, K. & Kotaka, T. 1988 Deformation of viscous droplets in an electric field: poly(propylene oxide)/poly(dimethylsiloxane) systems. Langmuir 4 (1), 170–175.CrossRefGoogle Scholar
O’Konski, C. T. & Thacher, H. C. 1953 The distortion of aerosol droplets by an electric field. J. Phys. Chem. 57 (9), 955–958.CrossRefGoogle Scholar
Prosperetti, A. 1980 Normal-mode analysis for the oscillations of a viscous-liquid drop in an immiscible liquid. J. Méc. 19 (1), 149–182.Google Scholar
Rosenkilde, C. E. 1969 A dielectric fluid drop in an electric field. Proc. R. Soc. Lond. A 312, 473–494.Google Scholar
Saville, D. A. 1997 Electrohydrodynamics: the Taylor–Melcher leaky dielectric model. Annu. Rev. Fluid Mech. 29, 27–64.CrossRefGoogle Scholar
Sherwood, J. D. 1988 Breakup of fluid droplets in electric and magnetic fields. J. Fluid Mech. 188, 133–146.CrossRefGoogle Scholar
Smith, C. V. & Melcher, J. R. 1967 Electrohydrodynamically induced spatially periodic cellular Stokes-flow. Phys. Fluids 10, 2315–2322.CrossRefGoogle Scholar
Sozou, C. 1973 Electrohydrodynamics of a liquid drop: the development of the flow field. Proc. R. Soc. Lond. A 334, 343–356.Google Scholar
Supeene, G., Koch, C. R. & Bhattacharjee, S. 2004 Deformation of a droplet in an electrical field: transient response in dielectric media. J. Comput. Theoret. Nanosci. 1 (4), 429–437.CrossRefGoogle Scholar
Supeene, G., Koch, C. R. & Bhattacharjee, S. 2008 Deformation of a droplet in an electric field: nonlinear transient response in perfect and leaky dielectric media. J. Colloid Interface Sci. 318 (2), 463–476.CrossRefGoogle Scholar
Taylor, G. I. 1964 Disintegration of water drops in an electric field. Proc. R. Soc. Lond. A 280, 383–397.Google Scholar
Taylor, G. I. 1966 Studies in electrohydrodynamics: I. The circulation produced in a drop by an electric field. Proc. R. Soc. Lond. A 291, 159–167.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146 (858), 501–523.Google Scholar
Torza, S., Cox, R. G. & Mason, S. G. 1971 Electrohydrodynamic deformation and burst of liquid drops. Phil. Trans. R. Soc. Lond. A 269, 295–319.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-Rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y.-J. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 169 (2), 708–759.CrossRefGoogle Scholar
Tsukada, T., Katayama, T., Ito, Y. & Hozawa, M. 1993 Theoretical and experimental studies of circulations inside and outside a deformed drop under a uniform electric field. J. Chem. Engng Japan 26 (6), 698–703.CrossRefGoogle Scholar
Vizika, O. & Saville, D. A. 1992 The electrohydrodynamic deformation of drops suspended in liquids in steady and oscillatory electric fields. J. Fluid Mech. 239, 1–21.CrossRefGoogle Scholar
Wilson, C. T. R. & Taylor, G. I. 1925 The bursting of soap bubbles in a uniform electric field. Proc. Camb. Phil. Soc. 22, 728–730.CrossRefGoogle Scholar
Yu, M., Lira, R. B., Riske, K. A., Dimova, R. & Lin, H. 2015 Ellipsoidal relaxation of deformed vesicles. Phys. Rev. Lett. 115 (12), 128303.CrossRefGoogle ScholarPubMed
Zeleny, J. 1915 On the conditions of instability of electrified drops, with applications to the electrical discharge from liquid points. Proc. Camb. Phil. Soc. 18, 71–83.Google Scholar
Zeleny, J. 1917 Instability of electrified liquid surfaces. Phys. Rev. 10, 1–6.CrossRefGoogle Scholar
Zeleny, J. 1920 Electrical discharges from pointed conductors. Phys. Rev. 16, 102–125.CrossRefGoogle Scholar
Zhang, J., Zahn, J. D. & Lin, H. 2013 Transient solution for droplet deformation under electric fields. Phys. Rev. E 87 (4), 043008.Google ScholarPubMed