Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T22:39:14.044Z Has data issue: false hasContentIssue false
  • English
  • Français

Thrust generation from pitching foils with flexible trailing edge flaps

Published online by Cambridge University Press:  31 August 2017

M. Jimreeves David ,
R. N. Govardhan Open the ORCID record for R. N. Govardhan [Opens in a new window]  and
J. H. Arakeri
M. Jimreeves David
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
R. N. Govardhan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
J. H. Arakeri
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore, 560012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present experimental study, we investigate thrust production from a pitching flexible foil in a uniform flow. The flexible foils studied comprise a rigid foil in the front (chord length 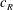$c_{R}$) that is pitched sinusoidally at a frequency 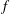$f$, with a flexible flap of length 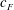$c_{F}$ and flexural rigidity 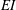$EI$ attached to its trailing edge. We investigate thrust generation for a range of flexural rigidities ($EI$) and flap length to total chord ratio (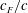$c_{F}/c$), with the mean thrust (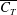$\overline{C_{T}}$) and the efficiency of thrust generation (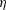$\unicode[STIX]{x1D702}$) being directly measured in each case. The thrust in the rigid foil cases, as expected, is found to be primarily due to the normal force on the rigid foil (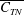$\overline{C_{TN}}$) with the chordwise or axial thrust contribution (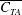$\overline{C_{TA}}$) being small and negative. In contrast, in the flexible foil cases, the axial contribution to thrust becomes important. We find that using a non-dimensional flexural rigidity parameter (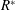$R^{\ast }$) defined as 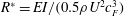$R^{\ast }=EI/(0.5\unicode[STIX]{x1D70C}U^{2}c_{F}^{3})$ appears to combine the independent effects of variations in 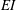$EI$ and 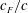$c_{F}/c$ at a given value of the reduced frequency (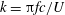$k=\unicode[STIX]{x03C0}fc/U$) for the range of 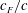$c_{F}/c$ values studied here (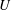$U$ is free-stream velocity; 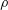$\unicode[STIX]{x1D70C}$ is fluid density). At 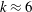$k\approx 6$, the peak mean thrust coefficient is found to be about 100 % higher than the rigid foil thrust, and occurs at 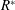$R^{\ast }$ value of approximately 8, while the peak efficiency is found to be approximately 300 % higher than the rigid foil efficiency and occurs at a distinctly different 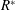$R^{\ast }$ value of close to 0.01. Corresponding to these two optimal flexural rigidity parameter values, we find two distinct flap deflection shapes; the peak thrust corresponding to a mode 1 type simple bending of the flap with no inflection points, while the peak efficiency corresponds to a distinctly different deflection profile having an inflection point along the flap. The peak thrust condition is found to be close to the ‘resonance’ condition for the first mode natural frequency of the flexible flap in still water. In both these optimal cases, we find that it is the axial contribution to thrust that dominates (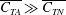$\overline{C_{TA}}\gg \overline{C_{TN}}$), in contrast to the rigid foil case. Particle image velocimetry (PIV) measurements for the flexible cases show significant differences in the strength and arrangement of the wake vortices in these two cases.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 70 - 103
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Bohl, D. G. & Koochesfahani, M. M. 2009 Mtv measurements of the vortical field in the wake of an airfoil oscillating at high reduced frequency. J. Fluid Mech. 620, 63–88.Google Scholar
Buchholz, J. H. J. & Smits, A. J. 2008 The wake structure and thrust performance of a rigid low-aspect-ratio pitching panel. J. Fluid Mech. 603, 331–365.CrossRefGoogle ScholarPubMed
Cleaver, D. J., Wang, Z. & Gursul, I. 2012 Bifurcating flows of plunging aerofoils at high Strouhal numbers. J. Fluid Mech. 708, 349–376.Google Scholar
Combes, S. A. & Daniel, T. L. 2003 Flexural stiffness in insect wings. J. Expl Biol. 206, 2989–2997.CrossRefGoogle ScholarPubMed
Dai, H., Luo, H., Ferreira De Sousa, P. J. S. A. & Doyle, J. F. 2012 Thrust performance of flexible low-aspect-ratio pitching plate. Phys. Fluids 24, 101903.CrossRefGoogle Scholar
Daniel, T. L. 1984 Unsteady aspects of aquatic locomotion. Am. Zool. 24 (1), 121–134.CrossRefGoogle Scholar
Das, P., Govardhan, R. N. & Arakeri, J. H. 2013 Effect of hinged leaflets on vortex pair generation. J. Fluid Mech. 730, 626–658.CrossRefGoogle Scholar
Dewey, P. A., Boschitsch, B. M., Moored, K. W., Stone, H. A. & Smits, A. J. 2013 Scaling laws for the thrust production of flexible pitching panels. J. Fluid Mech. 732, 29–46.Google Scholar
Eldredge, J. D., Toomey, J. & Medina, A. 2010 On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 659, 94–115.CrossRefGoogle Scholar
Godoy-Diana, R., Aider, J.-L. & Wesfreid, J. E. 2008 Transitions in the wake of a flapping foil. Phys. Rev. E 77 (1), 016308.Google Scholar
Govardhan, R. N. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.Google Scholar
Heathcote, S. & Gursul, I. 2007 Flexible flapping airfoil propulsion at low Reynolds numbers. AIAA J. 45, 1066–1079.CrossRefGoogle Scholar
Kang, C.-K., Aono, H., Cesnik, C. E. S. & Shyy, W. 2011 Effects of flexibility on the aerodynamic performance of flapping wings. J. Fluid Mech. 689, 32–74.CrossRefGoogle Scholar
Katz, J. & Weihs, D. 1978 Hydrodynamic propulsion by large amplitude oscillation of an airfoil with chordwise flexibility. J. Fluid Mech. 88 (03), 485–497.CrossRefGoogle Scholar
Kim, D. & Gharib, M. 2011 Flexibility effects on vortex formation of translating plates. J. Fluid Mech. 677, 255–271.CrossRefGoogle Scholar
Koochesfahani, M. M. 1989 Vortical patterns in wake of an oscillating air foil. AIAA J. 27, 1200–1205.CrossRefGoogle Scholar
Lauder, G. V., Madden, P. G. A., Tangorra, J. L., Anderson, E. & Baker, T. V. 2011 Bioinspiration from fish for smart material design and function. Smart Materials Structures 20 (9), 094014.Google Scholar
Lewin, G. C. & Haj-Hariri, H. 2003 Modelling thrust generation of a two-dimensional heaving airfoil in a viscous flow. J. Fluid Mech. 492, 339–362.CrossRefGoogle Scholar
Lighthill, M. J. 1970 Aquatic animal propulsion of high hydromechanical efficiency. J. Fluid Mech. 44 (02), 265–301.CrossRefGoogle Scholar
Low, K. H. 2011 Current and future trends of biologically inspired underwater vehicles. In Defense Science Research Conference and Expo (DSR), 2011, pp. 1–8. IEEE.Google Scholar
Lu, K., Xie, Y. H. & Zhang, D. 2013 Numerical study of large amplitude, nonsinusoidal motion and camber effects on pitching airfoil propulsion. J. Fluids Struct. 36, 184–194.Google Scholar
Mackowski, A. W. & Williamson, C. H. K. 2015 Direct measurement of thrust and efficiency of an airfoil undergoing pure pitching. J. Fluid Mech. 765, 524–543.CrossRefGoogle Scholar
Marais, C., Thiria, B., Wesfreid, J. E. & Godoy-Diana, R. 2012 Stabilizing effect of flexibility in the wake of a flapping foil. J. Fluid Mech. 710, 659–669.CrossRefGoogle Scholar
McCroskey, W. J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14 (1), 285–311.Google Scholar
Michelin, S. & Llewellyn Smith, S. G. 2009 Resonance and propulsion performance of a heaving flexible wing. Phys. Fluids 21, 071902.Google Scholar
Paraz, F., Eloy, C. & Schouveiler, L. 2014 Experimental study of the response of a flexible plate to a harmonic forcing in a flow. C. R. Méc. 342 (9), 532–538.Google Scholar
Paraz, F., Schouveiler, L. & Eloy, C. 2016 Thrust generation by a heaving flexible foil: resonance, nonlinearities, and optimality. Phys. Fluids 28 (1), 011903.Google Scholar
Platzer, M. F., Jones, K. D., Young, J. & Lai, J. C. S. 2008 Flapping wing aerodynamics: progress and challenges. AIAA J. 46 (9), 2136–2149.CrossRefGoogle Scholar
Prempraneerach, P., Hover, F. S. & Triantafyllou, M. S. 2004 The effect of chordwise flexibility on the thrust and efficiency of a flapping foil. In 13th International Symposium of Unmanned Untethered Submersible Techn.Google Scholar
Quinn, D. B., Lauder, G. V. & Smits, A. J. 2014 Scaling the propulsive performance of heaving flexible panels. J. Fluid Mech. 738, 250–267.Google Scholar
Ramananarivo, S., Godoy-Diana, R. & Thiria, B. 2011 Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl Acad. Sci. USA 108 (15), 5964–5969.Google Scholar
Sarkar, S. & Venkatraman, K. 2006 Numerical simulation of thrust generating flow past a pitching foil. Comput. Fluids 35, 16–42.Google Scholar
Schnipper, T., Andersen, A. & Bohr, T. 2009 Vortex wakes of a flapping foil. J. Fluid Mech. 633, 411–423.CrossRefGoogle Scholar
Shinde, S. Y. & Arakeri, J. H. 2014 Flexibility in flapping foil suppresses meandering of induced jet in absence of free stream. J. Fluid Mech. 757, 231–250.CrossRefGoogle Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C. K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46 (7), 284–327.CrossRefGoogle Scholar
Thiria, B. & Godoy-Diana, R. 2010 How wing compliance drives the efficiency of self-propelled flapping flyers. Phys. Rev. E 82 (1), 015303.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32 (1), 33–53.Google Scholar
Vanella, M., Fitzgerald, T., Preidikman, S., Balaras, E. & Balachandran, B. 2009 Influence of flexibility on the aerodynamic performance of a hovering wing. J. Expl Biol. 212 (1), 95–105.CrossRefGoogle ScholarPubMed
Wang, Z. 2000 Vortex shedding and frequency selection in flapping flight. J. Fluid Mech. 410, 323–341.CrossRefGoogle Scholar
Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.Google Scholar
Wu, T. 1971 Hydromechanics of swimming propulsion. Part 1. Swimming of a two-dimensional flexible plate at variable forward speeds in an inviscid fluid. J. Fluid Mech. 46 (02), 337–355.Google Scholar