Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Browne, Oliver M.
Haas, Anthony P.
Fasel, Hermann F.
and
Brehm, Christoph
2020.
A Nonlinear Wavepacket Tracking Method for Hypersonic Boundary-Layer Flows on Irregular Domains.
Zhang, Chuanhong
2020.
Evolution of the second mode in a hypersonic boundary layer.
Physics of Fluids,
Vol. 32,
Issue. 12,
Hader, Christoph
Leinemann, Madlen
and
Fasel, Hermann F.
2020.
Direct Numerical Simulations of Hypersonic Boundary-Layer Transition for a slender cone.
Unnikrishnan, S.
and
Gaitonde, Datta V.
2020.
Linear, nonlinear and transitional regimes of second-mode instability.
Journal of Fluid Mechanics,
Vol. 905,
Issue. ,
Dong, Siwei
Chen, Jianqiang
Yuan, Xianxu
Chen, Xi
and
Xu, Guoliang
2020.
Wall pressure beneath a transitional hypersonic boundary layer over an inclined straight circular cone.
Advances in Aerodynamics,
Vol. 2,
Issue. 1,
Khan, Arham Amin
Kuehl, Joseph
and
Chelidze, David
2020.
Toward a unified interpretation of the “proper”/“smooth” orthogonal decompositions and “state variable”/“dynamic mode” decompositions with application to fluid dynamics.
AIP Advances,
Vol. 10,
Issue. 3,
Hader, Christoph
and
Fasel, Hermann F.
2021.
Direct Numerical Simulations of Hypersonic Boundary-Layer Transition for a Straight Cone at Mach 4: Oblique Breakdown.
Chen, Jianqiang
Dong, Siwei
Chen, Xi
Yuan, Xianxu
and
Xu, Guoliang
2021.
Stationary cross-flow breakdown in a high-speed swept-wing boundary layer.
Physics of Fluids,
Vol. 33,
Issue. 2,
Hader, Christoph
and
Fasel, Hermann F.
2021.
Flow control using steady blowing and suction strips in a Mach 6 Boundary Layer on a Flared Cone.
Singh, Ashish
Threadgill, James A.
Flood, John T.
Craig, Stuart A.
Little, Jesse C.
Hader, Christoph
and
Fasel, Hermann F.
2021.
Development of Plasma-based Controlled Disturbances for the Study of Boundary Layer Transition and Shock Boundary Layer Interaction.
Hader, Christoph
and
Fasel, Hermann F.
2021.
Direct Numerical Simulations of Hypersonic Boundary-Layer Transition for a Straight Cone at Mach 7.
Leinemann, Madlen
Hader, Christoph
and
Fasel, Hermann F.
2021.
Direct Numerical Simulations of the Nonlinear Boundary Layer Transition Regime on a Flat Plate at Mach 6.
Zhang, Chuanhong
and
Shi, Zhiwei
2021.
Nonlinear interactions in a hypersonic boundary layer.
AIP Advances,
Vol. 11,
Issue. 3,
Hader, Christoph
Deng, Ning
and
Fasel, Hermann F.
2021.
Direct Numerical Simulations of Hypersonic Boundary-Layer Transition for a straight cone at Mach 5.
Zhu, Yiding
Zhu, Wenkai
Gu, Dingwei
Lee, Cunbiao
and
Smith, C. R.
2021.
Characteristics of transition to turbulence over a Mach 6 flared cone.
Physics of Fluids,
Vol. 33,
Issue. 10,
Hader, Christoph
and
Fasel, Hermann F.
2021.
Three-dimensional wave packets in a Mach 10 Boundary Layer on a Sharp Cone.
Hader, Christoph
Deng, Ning
Woodward, Michael
and
Fasel, Hermann F.
2021.
Direct Numerical Simulations of Laminar-Turbulent Transition for Transonic Boundary Layers.
Groot, Koen J.
Patel, Jay
Saiyasak, Caleb
Coder, James G.
Stefanski, Douglas L.
and
Reed, Helen L.
2021.
Assessment of the Amplification Factor Transport Transition Model for High-Mach Number Flows.
Biella, Massimo
Hader, Christoph
and
Fasel, Hermann F.
2022.
Numerical investigation of the laminar-turbulent transition process for the HIFiRE-1 Flight Test.
Hader, Christoph
and
Fasel, Hermann F.
2022.
Flow control using steady blowing and suction strips in a Mach 6 Boundary Layer on a Flared Cone: “Natural” Transition.
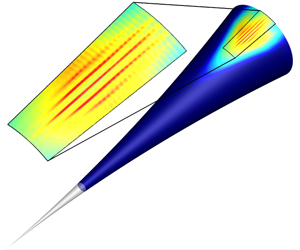
 $k_{c}$) and to include shallow instability waves with small azimuthal wavenumbers. The simulation results indicated that the wave packet development was dominated by axisymmetric and shallow (small
$k_{c}$) and to include shallow instability waves with small azimuthal wavenumbers. The simulation results indicated that the wave packet development was dominated by axisymmetric and shallow (small  $k_{c}$) second-mode waves for a large downstream extent. Towards the downstream end of the computational domain a rapid broadening of the disturbance amplitude spectra was observed, which is an indication that the wave packet reached the strongly nonlinear stages. The disturbance spectra of the nonlinear regime, and the downstream amplitude development of the dominant disturbance wave components, provided conclusive evidence that the so-called fundamental breakdown was the dominant nonlinear mechanism. Furthermore, contours of the time-averaged Stanton number exhibited ‘hot’ streaks within the wave packet on the surface of the cone. Hot streaks have also been observed in the Purdue flared cone experiments using temperature sensitive paint (TSP) and in numerical investigations using DNS. The azimuthal streak spacing obtained from the wave packet simulation agrees well with that observed in the Purdue quiet tunnel experiments.
$k_{c}$) second-mode waves for a large downstream extent. Towards the downstream end of the computational domain a rapid broadening of the disturbance amplitude spectra was observed, which is an indication that the wave packet reached the strongly nonlinear stages. The disturbance spectra of the nonlinear regime, and the downstream amplitude development of the dominant disturbance wave components, provided conclusive evidence that the so-called fundamental breakdown was the dominant nonlinear mechanism. Furthermore, contours of the time-averaged Stanton number exhibited ‘hot’ streaks within the wave packet on the surface of the cone. Hot streaks have also been observed in the Purdue flared cone experiments using temperature sensitive paint (TSP) and in numerical investigations using DNS. The azimuthal streak spacing obtained from the wave packet simulation agrees well with that observed in the Purdue quiet tunnel experiments.