Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jiang, Hongyi
and
Cheng, Liang
2018.
Hydrodynamic characteristics of flow past a square cylinder at moderate Reynolds numbers.
Physics of Fluids,
Vol. 30,
Issue. 10,
Lin, L.M.
Shi, S.Y.
and
Wu, Y.X.
2018.
Intrinsic relationship of vorticity between modes A and B in the wake of a bluff body.
Theoretical and Applied Mechanics Letters,
Vol. 8,
Issue. 5,
p.
320.
Lin, L. M.
Shi, S. Y.
and
Wu, Y. X.
2019.
Physical mechanism for origin of streamwise vortices in mode A of a square-section cylinder.
Acta Mechanica Sinica,
Vol. 35,
Issue. 2,
p.
411.
Zafar, Farhan
and
Alam, Md. Mahbub
2019.
Flow structure around and heat transfer from cylinders modified from square to circular.
Physics of Fluids,
Vol. 31,
Issue. 8,
Qu, Yuan
Wang, Jinjun
Feng, Lihao
and
He, Xi
2019.
Effect of excitation frequency on flow characteristics around a square cylinder with a synthetic jet positioned at front surface.
Journal of Fluid Mechanics,
Vol. 880,
Issue. ,
p.
764.
Lin, L. M.
and
Tan, Z. R.
2019.
DNS in evolution of vorticity and sign relationship in wake transition of a circular cylinder: (pure) mode A.
Acta Mechanica Sinica,
Vol. 35,
Issue. 6,
p.
1131.
Lin, L. M.
Shi, S. Y.
Zhong, X. F.
and
Wu, Y. X.
2019.
Mechanism of wavy vortex and sign laws in flow past a bluff body: vortex-induced vortex.
Acta Mechanica Sinica,
Vol. 35,
Issue. 1,
p.
1.
Zhang, Zhanbiao
and
Xu, Fuyou
2020.
Spanwise length and mesh resolution effects on simulated flow around a 5:1 rectangular cylinder.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 202,
Issue. ,
p.
104186.
Tan, Kin Jon Benjamin
Hesse, Henrik
and
Wang, Peng Cheng
2020.
Numerical Capture and Validation of a Massively Separated Bluff-Body Wake.
Jiang, Hongyi
2020.
Separation angle for flow past a circular cylinder in the subcritical regime.
Physics of Fluids,
Vol. 32,
Issue. 1,
Hernández, R.H.
and
Tapia, L.
2020.
Vortex dynamics and scalar transport in the wake of a flat-plate controlled by a vibrating trailing-edge flap.
International Journal of Heat and Fluid Flow,
Vol. 81,
Issue. ,
p.
108526.
Tanweer, Sartaj
Dewan, Anupam
and
Sanghi, Sanjeev
2020.
Influence of three-dimensional wake transition on heat transfer from a square cylinder near a moving wall.
International Journal of Heat and Mass Transfer,
Vol. 148,
Issue. ,
p.
118986.
Zhu, Hongjun
Tang, Tao
and
Wang, Junlei
2020.
Modification of wake flow and air-bubble-vortex interference in the flow control of a circular cylinder with a pair of air jets: Effect of injection velocity.
Ocean Engineering,
Vol. 214,
Issue. ,
p.
107766.
Jiang, Hongyi
and
Cheng, Liang
2020.
Transition to chaos in the cylinder wake through the Mode C flow.
Physics of Fluids,
Vol. 32,
Issue. 1,
Yang, Hanbin
Yang, Wanli
Yang, Tong
and
Li, Qiao
2020.
Experimental investigation of flow around a square cylinder with very small aspect ratios.
Ocean Engineering,
Vol. 214,
Issue. ,
p.
107732.
Sanyal, Aniruddha
and
Dhiman, Amit
2020.
Shear-induced viscosity stratified flow past a pair of heated side-by-side square cylinders in a confined domain.
Physics of Fluids,
Vol. 32,
Issue. 5,
Jiang, Hongyi
and
Cheng, Liang
2020.
Flow separation around a square cylinder at low to moderate Reynolds numbers.
Physics of Fluids,
Vol. 32,
Issue. 4,
Arif, Md. Reyaz
and
Hasan, Nadeem
2020.
Large-scale heating effects on global parameters for flow past a square cylinder at different cylinder inclinations.
International Journal of Heat and Mass Transfer,
Vol. 161,
Issue. ,
p.
120237.
Sen, Uddalok
Sarkar, Sourav
Bagchi, Sombuddha
Mukhopadhyay, Achintya
and
Sen, Swarnendu
2020.
Innovations in Sustainable Energy and Cleaner Environment.
p.
411.
Zhang, Yuhang
Wang, Rui
Chen, Yaoran
Bao, Yan
Han, Zhaolong
Zhou, Dai
Ping, Huan
Fu, Shixiao
and
Zhao, Yongsheng
2020.
Three-dimensional wake transition in the flow over four square cylinders at low Reynolds numbers.
AIP Advances,
Vol. 10,
Issue. 1,
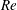 $Re$) of 165.7. A gradual wake transition from Mode A* (i.e. Mode A with vortex dislocations) to Mode B is observed over a range of
$Re$) of 165.7. A gradual wake transition from Mode A* (i.e. Mode A with vortex dislocations) to Mode B is observed over a range of 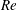 $Re$ from 185 to 210, within which the probability of occurrence of vortex dislocations decreases monotonically with increasing
$Re$ from 185 to 210, within which the probability of occurrence of vortex dislocations decreases monotonically with increasing 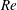 $Re$. The characteristics of the Strouhal–Reynolds number relationship are analysed. At the onset of Mode A*, a sudden drop of the 3-D Strouhal number from its two-dimensional counterpart is observed, which is due to the subcritical nature of the Mode A* instability. A continuous 3-D Strouhal–Reynolds number curve is observed over the mode swapping regime, since Mode A* and Mode B have extremely close vortex shedding frequencies and therefore only a single merged peak is observed in the frequency spectrum. The existence of hysteresis for the Mode A and Mode B wake instabilities is examined. The unconfined Mode A and Mode B wake instabilities are hysteretic and non-hysteretic, respectively. However, a spanwise confined Mode A could be non-hysteretic. It is proposed that the existence of hysteresis at a wake instability can be identified by examining the sudden/gradual variation of the 3-D flow properties at the onset of the wake instability, with sudden and gradual variations corresponding to hysteretic (subcritical) and non-hysteretic (supercritical) flows, respectively.
$Re$. The characteristics of the Strouhal–Reynolds number relationship are analysed. At the onset of Mode A*, a sudden drop of the 3-D Strouhal number from its two-dimensional counterpart is observed, which is due to the subcritical nature of the Mode A* instability. A continuous 3-D Strouhal–Reynolds number curve is observed over the mode swapping regime, since Mode A* and Mode B have extremely close vortex shedding frequencies and therefore only a single merged peak is observed in the frequency spectrum. The existence of hysteresis for the Mode A and Mode B wake instabilities is examined. The unconfined Mode A and Mode B wake instabilities are hysteretic and non-hysteretic, respectively. However, a spanwise confined Mode A could be non-hysteretic. It is proposed that the existence of hysteresis at a wake instability can be identified by examining the sudden/gradual variation of the 3-D flow properties at the onset of the wake instability, with sudden and gradual variations corresponding to hysteretic (subcritical) and non-hysteretic (supercritical) flows, respectively.