Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-23T10:56:47.447Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional structural characteristics of flow separation induced by a forward-facing step in a turbulent channel flow

Published online by Cambridge University Press:  26 May 2021

Xingjun Fang Open the ORCID record for Xingjun Fang [Opens in a new window] ,
Mark F. Tachie Open the ORCID record for Mark F. Tachie [Opens in a new window] ,
Donald J. Bergstrom ,
Zixuan Yang Open the ORCID record for Zixuan Yang [Opens in a new window]  and
Bing-Chen Wang Open the ORCID record for Bing-Chen Wang [Opens in a new window]
Xingjun Fang*
Affiliation:
Department of Mechanical Engineering, University of Manitoba, Winnipeg, MBR3T 5V6, Canada
Mark F. Tachie
Affiliation:
Department of Mechanical Engineering, University of Manitoba, Winnipeg, MBR3T 5V6, Canada
Donald J. Bergstrom
Affiliation:
Department of Mechanical Engineering, University of Saskatchewan, Saskatoon, SKS7N 5A9, Canada
Zixuan Yang
Affiliation:
Institute of Mechanics, Chinese Academy of Sciences, Beijing100190, PR China
Bing-Chen Wang
Affiliation:
Department of Mechanical Engineering, University of Manitoba, Winnipeg, MBR3T 5V6, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

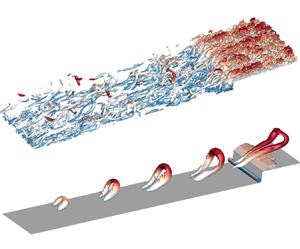
Separating and reattaching turbulent flows induced by a forward-facing step subjected to an incoming fully developed turbulent channel flow are studied using direct numerical simulation. The step height is one quarter of the channel height, and the Reynolds number based on friction velocity and half-channel height at the inlet is 180. The three-dimensional spatio-temporal characteristics of separation bubbles upstream and downstream of the step are analysed with particular attention to the effects of impinging hairpin structures and the topology of principal stretching. Immediately upstream of the step, the fluctuating vorticity parallel to the mean streamlines is significant. On the frontal surface of the step, strong spanwise skin friction appears in the form of alternating positive and negative values in vertical strips. Over the step, the principal stretching switches orientation along a curve emanating from the leading edge, which is termed the principal stretching line (PSL). The reverse flows upstream and downstream of the step possess dominant and harmonic frequencies that mirror those of the incoming flow. As a hairpin structure leans over the step, the associated vorticity is deformed by the principal stretching. Specifically, PSL marks the lower bound of the deformed hairpin legs, and an opposite-signed pair of counter-rotating quasi-streamwise vortices are induced near the top surface of the step. Consequently, the separation bubbles upstream of and over the step are enlarged and suppressed, respectively. For a sufficiently strong hairpin structure interacting with the step, an open-type separation occurs upstream of the step, while dual separation bubbles appear over the step.

JFM classification

Boundary Layers: Boundary layer separation Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 919 , 25 July 2021 , A24
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abu-Mulaweh, H.I., Armaly, B.F. & Chen, T.S. 1996 Laminar nature convection flow over a vertical forward-facing step. J. Thermophys. Heat Transfer 10 (3), 517–523.CrossRefGoogle Scholar
Acarlar, M.S. & Smith, C.R. 1987 a A study of hairpin vortices in a laminar boundary layer. Part 1. hairpin vortices generated by a hemisphere proturberance. J. Fluid Mech. 175, 1–41.CrossRefGoogle Scholar
Acarlar, M.S. & Smith, C.R. 1987 b A study of hairpin vortices in a laminar boundary layer. Part 2. hairpin vortices generated by fluid injection. J. Fluid Mech. 175, 43–83.CrossRefGoogle Scholar
Addad, Y., Laurence, D., Talotte, C. & Jacob, M.C. 2003 Large eddy simulation of forward-backward facing step for acoustic source identification. Intl J. Heat Fluid Flow 24, 562–571.CrossRefGoogle Scholar
Adrian, R.J., Meinhart, C.D. & Tomkins, C.D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Adrian, R.J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
Alam, M. & Sandham, N.D. 2000 Direct numerical simulation of ‘short’ laminar separation bubbles with turbulent reattachment. J. Fluid Mech. 410, 1–28.CrossRefGoogle Scholar
Bernard, P.S., Thomas, J.M. & Handler, R.A. 1993 Vortex dynamics and the production of Reynolds stress. J. Fluid Mech. 253, 385–419.CrossRefGoogle Scholar
Blackburn, H.M., Lee, D., Albrecht, T. & Singh, J. 2019 Semtex: a spectral element-Fourier solver for the incompressible Navier–Stokes equations in cylindrical or Cartesian coordinates. Comput. Phys. Commun. 245, 106804.CrossRefGoogle Scholar
Blackburn, H.M. & Sherwin, S.J. 2004 Formulation of a Galerkin spectral element-Fourier method for three-dimensional incompressible flows in cylindrical geometries. J. Comput. Phys. 197 (2), 759–778.CrossRefGoogle Scholar
Brooke, J.W. & Hanratty, T.J. 1993 Origin of turbulence-producing eddies in a channel flow. Phys. Fluids 5 (4), 1011–1022.CrossRefGoogle Scholar
Camussi, R., Felli, M., Pereira, F., Aloisio, G. & Di Marco, A. 2008 Statistical properties of wall pressure fluctuations over a forward-facing step. Phys. Fluids 20, 075113.CrossRefGoogle Scholar
Chiba, K., Ishida, R. & Nakamura, K. 1995 Mechanism for entry flow instability through a forward-facing step channel. J. Non-Newtonian Fluid Mech. 57, 271–282.CrossRefGoogle Scholar
Dehtyriov, D., Hourigan, K. & Thompson, M.C. 2020 Direct numerical simulation of a counter-roating vortex pair interacting with a wall. J. Fluid Mech. 884, A36.CrossRefGoogle Scholar
Dianat, M. & Castro, I.P. 1984 Fluctuating surface shear stresses on bluff bodies. J. Wind Engng Ind. Aerodyn. 17, 133–146.CrossRefGoogle Scholar
Djilali, N. & Gartshore, I.S. 1991 Turbulent flow around a bluff rectangular plate. Part I: experimental investigation. Trans. ASME: J. Fluids Engng 113 (1), 51–59.Google Scholar
Eaton, J.K. & Johnston, J.P. 1982 Low frequency unsteadiness of a reattaching turbulent shear layer. In Turbulent Shear Flows (ed. L.J.S. Bradbury et al.), vol. 3, pp. 162–170. Springer.CrossRefGoogle Scholar
Fang, X. 2017 The influences of V-shaped ribs and spanwise system rotation on a turbulent square duct flow. Ph.D. thesis, University of Manitoba, Department of Mechanical Engineering.Google Scholar
Fang, X. & Tachie, M.F. 2019 a Flows over surface-mounted bluff bodies with different spanwise widths submerged in a deep turbulent boundary layer. J. Fluid Mech. 877, 717–758.CrossRefGoogle Scholar
Fang, X. & Tachie, M.F. 2019 b On the unsteady characteristics of turbulent separations over a forward-backward-facing step. J. Fluid Mech. 863, 994–1030.CrossRefGoogle Scholar
Fang, X. & Tachie, M.F. 2020 Spatio-temporal dynamics of flow separation induced by a forward-facing step submerged in a thick turbulent boundary layer. J. Fluid Mech. 892, A40.CrossRefGoogle Scholar
Fang, X., Tachie, M.F. & Bergstrom, D.J. 2021 Direct numerical simulation of turbulent flow separation induced by a forward-facing step. Intl J. Heat Fluid Flow 87, 108753.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2010 Hierachy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemens, N.T. & Dolling, D.S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.CrossRefGoogle Scholar
Goudar, M.V., Breugem, W. -P. & Elsinga, G.E. 2016 Auto-generation in wall turbulence by the interaction of weak eddies. Phys. Fluids 28, 035111.CrossRefGoogle Scholar
Graziani, A., Kerhervé, F., Martinuzzi, R.J. & Keirsbulck, L. 2018 Dynamics of the recirculating areas of a forward-facing step. Exp. Fluids 59, 154.CrossRefGoogle Scholar
Hattori, H. & Nagano, Y. 2010 Investigation of turbulent boundary layer over forward-facing step via direct numerical simulation. Intl J. Heat Fluid Flow 31 (3), 284–294.CrossRefGoogle Scholar
Hudy, L.M., Naguib, A.M. & Humphreys, W.M. 2003 Wall-pressure-array measurements beneath a separating/reattaching flow region. Phys. Fluids 15 (3), 706–717.CrossRefGoogle Scholar
Humble, R.A., Scarano, F. & Van Oudheusden, B.W. 2009 Unsteady aspects of an incident shock wave/turbulent boundary layer interaction. J. Fluid Mech. 635, 47–74.CrossRefGoogle Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.CrossRefGoogle Scholar
Jodai, Y. & Elsinga, G.E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.CrossRefGoogle Scholar
Karniadakis, G.E., Israeli, M. & Orszag, S.A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Kevin, M.J. & Hutchins, N. 2019 Turbulent structures in a statistically three-dimensional boundary layer. J. Fluid Mech. 859, 543–565.CrossRefGoogle Scholar
Kim, K., Sung, H.J. & Adrian, R.J. 2008 Effects of background noise on generating coherent packets of hairpin vortices. Phys. Fluids 20, 105107.CrossRefGoogle Scholar
Kim, K.C., Ji, H.S. & Seong, S.H. 2003 Flow structure around a 3-D rectangular prism in a turbulent boundary layer. J. Wind Engng Ind. Aerodyn. 91, 653–669.CrossRefGoogle Scholar
Kiya, M. & Sasaki, K. 1983 Structure of a turbulent separation bubble. J. Fluid Mech. 137, 83–113.CrossRefGoogle Scholar
Lanzerstorfer, D. & Kuhlmann, H.C. 2012 Three-dimensional instability of the flow over a forward-facing step. J. Fluid Mech. 695, 390–404.CrossRefGoogle Scholar
Marino, L. & Luchini, P. 2009 Adjoint analysis of the flow over a forward-facing step. Theor. Comput. Fluid Dyn. 23, 37–54.CrossRefGoogle Scholar
Martinuzzi, R. & Tropea, C. 1993 The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. Trans. ASME: J. Fluids Engng 115, 85–92.Google Scholar
Mohammed-Taifour, A. & Weiss, J. 2016 Unsteadiness in a large turbulent separation bubble. J. Fluid Mech. 799, 383–412.CrossRefGoogle Scholar
Moser, R.D., Kim, J. & Mansour, N.N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_\tau =590$. Phys. Fluids 11 (4), 943–945.CrossRefGoogle Scholar
Moss, W.D. & Baker, S. 1980 Re-circulating flows associated with two-dimensional steps. Aeronaut. Q. 31 (3), 151–172.CrossRefGoogle Scholar
Muralidhar, S.D., Podvin, B., Mathelin, L. & Fraigneau, Y. 2019 Spatial-temporal proper orthogonal decomposition of turbulent channel flow. J. Fluid Mech. 864, 614–639.CrossRefGoogle Scholar
Pearson, D.S., Goulart, P.J. & Ganapathisubramani, B. 2013 Turbulent separation upstream of a forward-facing step. J. Fluid Mech. 724, 284–304.CrossRefGoogle Scholar
Ren, H. & Wu, Y. 2011 Turbulent boundary layers over smooth and rough forward-facing steps. Phys. Fluids 23, 045102.CrossRefGoogle Scholar
Schröder, A., Willert, C., Schanz, D., Geisler, R., Jahn, T., Gallas, Q. & Leclaire, B. 2020 The flow around a surface mounted cube: a characterization by time-resolved PIV, 3D Shake-The-Box and LBM simulation. Exp. Fluids 61, 189.CrossRefGoogle Scholar
Sherry, M., Lo Jacono, D. & Sheridan, J. 2010 An experimental investigation of the recirculation zone formed downstream of a forward facing step. J. Wind Engng Ind. Aerodyn. 98 (12), 888–894.CrossRefGoogle Scholar
Stüer, H., Gyr, A. & Kinzelbach, W. 1999 Laminar separation on a forward facing step. Eur. J. Mech. B/Fluids 18, 675–692.CrossRefGoogle Scholar
Tafti, D.K. & Vanka, S.P. 1991 A three-dimensional numerical study of flow separation and reattachment on a blunt plate. Phys. Fluids A 3, 2887–2909.CrossRefGoogle Scholar
Thacker, A., Aubrun, S., Leroy, A. & Devinant, P. 2013 Experimental characterization of flow unsteadiness in the centerline plane of an Ahmed body rear slant. Exp. Fluids 54, 1479.CrossRefGoogle Scholar
Wilhelm, D., Härtel, C. & Kleiser, L. 2003 Computational analysis of the two-dimensional-three- dimensional transition in forward-facing step flow. J. Fluid Mech. 489, 1–27.CrossRefGoogle Scholar
Yang, Z. & Voke, P.R. 2001 Large-eddy simulation of boundary-layer separation and transition at a change of surface curvature. J. Fluid Mech. 439, 305–333.CrossRefGoogle Scholar
Zhou, J., Adrian, R.J., Balachandar, S. & Kendall, T.M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar

Fang et al. supplementary movie

Animated figure 4

Download Fang et al. supplementary movie(Video)
Video 13.2 MB