Article contents
Three-dimensional small-scale instabilities of plane internal gravity waves
Published online by Cambridge University Press: 29 January 2019
Abstract
We study the evolution of three-dimensional (3-D), small-scale, small-amplitude perturbations on a plane internal gravity wave using the local stability approach. The plane internal wave is characterised by its non-dimensional amplitude, 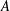 $A$, and the angle the group velocity vector makes with gravity,
$A$, and the angle the group velocity vector makes with gravity, 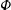 $\unicode[STIX]{x1D6F7}$. For a given
$\unicode[STIX]{x1D6F7}$. For a given  $(A,\unicode[STIX]{x1D6F7})$, the local stability equations are solved on the periodic fluid particle trajectories to obtain growth rates for all two-dimensional (2-D) and 3-D perturbation wave vectors. For small
$(A,\unicode[STIX]{x1D6F7})$, the local stability equations are solved on the periodic fluid particle trajectories to obtain growth rates for all two-dimensional (2-D) and 3-D perturbation wave vectors. For small 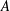 $A$, the local stability approach recovers previous results of 2-D parametric subharmonic instability (PSI) while offering new insights into 3-D PSI. Higher-order triadic resonances, and associated deviations from them, are also observed at small
$A$, the local stability approach recovers previous results of 2-D parametric subharmonic instability (PSI) while offering new insights into 3-D PSI. Higher-order triadic resonances, and associated deviations from them, are also observed at small 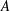 $A$. Moreover, for small
$A$. Moreover, for small 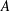 $A$, purely transverse instabilities resulting from parametric resonance are shown to occur at select values of
$A$, purely transverse instabilities resulting from parametric resonance are shown to occur at select values of 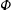 $\unicode[STIX]{x1D6F7}$. The possibility of a non-resonant instability mechanism for transverse perturbations at finite
$\unicode[STIX]{x1D6F7}$. The possibility of a non-resonant instability mechanism for transverse perturbations at finite 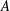 $A$ allows us to derive a heuristic, modified gravitational instability criterion. We then study the extension of small
$A$ allows us to derive a heuristic, modified gravitational instability criterion. We then study the extension of small 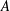 $A$ to finite
$A$ to finite 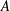 $A$ internal wave instabilities, where we recover and build upon existing knowledge of small-scale, small-amplitude internal wave instabilities. Four distinct regions of the
$A$ internal wave instabilities, where we recover and build upon existing knowledge of small-scale, small-amplitude internal wave instabilities. Four distinct regions of the 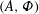 $(A,\unicode[STIX]{x1D6F7})$-plane based on the dominant instability modes are identified: 2-D PSI, 3-D oblique, quasi-2-D shear-aligned, and 3-D transverse. Our study demonstrates the local stability approach as a physically insightful and computationally efficient tool, with potentially broad utility for studies that are based on other theoretical approaches and numerical simulations of small-scale instabilities of internal waves in various settings.
$(A,\unicode[STIX]{x1D6F7})$-plane based on the dominant instability modes are identified: 2-D PSI, 3-D oblique, quasi-2-D shear-aligned, and 3-D transverse. Our study demonstrates the local stability approach as a physically insightful and computationally efficient tool, with potentially broad utility for studies that are based on other theoretical approaches and numerical simulations of small-scale instabilities of internal waves in various settings.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 10
- Cited by


