Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T07:54:50.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermally driven Marangoni surfers

Published online by Cambridge University Press:  09 July 2014

Alois Würger
Alois Würger*
Affiliation:
Laboratoire Ondes et Matière d’Aquitaine, CNRS – Université de Bordeaux, 351 Cours de la Libération, 33405 Talence, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

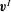We study autopropulsion of an interface particle that is driven by the Marangoni stress arising from a self-generated asymmetric temperature or concentration field. We calculate separately the long-range Marangoni flow $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\boldsymbol {v}}^{I}$ due to the stress discontinuity at the interface and the short-range velocity field 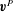${\boldsymbol {v}}^{P}$ imposed by the no-slip condition on the particle surface. Both contributions are evaluated for a spherical floater with temperature monopole and dipole moments. We find that the self-propulsion velocity is given by the amplitude of the ‘source doublet’ that belongs to the short-range contribution 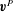${\boldsymbol {v}}^{P}$. Hydrodynamic interactions, on the other hand, are determined by the long-range Marangoni flow 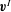${\boldsymbol {v}}^{I}$. Its dipolar part results in an asymmetric advection pattern of neighbouring particles, which in turn may perturb the known hexatic lattice or even favour disordered states.

JFM classification

Interfacial Flows (free surface): Capillary flows Complex Fluids: Colloids Drops and Bubbles: Thermocapillarity
Type
Papers
Information
Journal of Fluid Mechanics , Volume 752 , 10 August 2014 , pp. 589 - 601
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bickel, T., Majee, A. & Würger, A. 2013 Flow pattern in the vicinity of self-propelling hot Janus particles. Phys. Rev. E 88, 012301.CrossRefGoogle ScholarPubMed
Bickel, T., Zecua, G. & Würger, A. 2014 Polarization of active Janus particles. Phys. Rev. E 89, 050303(R).Google Scholar
Blake, J. R. & Chwang, A. T. 1974 Fundamental singularities of viscous flow. J. Engng Maths 8, 23–29.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16, 242–251.CrossRefGoogle Scholar
Howse, J. R., Jones, R. A. L., Ryan, A. J., Gough, T., Vafabakhsh, R. & Golestanian, R. 2007 Self-motile colloidal particles: from directed propulsion to random walk. Phys. Rev. Lett. 99, 048102.Google Scholar
Lauga, E. & Davis, A. M. 2012 Viscous Marangoni propulsion. J. Fluid Mech. 705, 120–133.Google Scholar
Masoud, H. & Shelley, M. 2014 Collective surfing of chemically active particles. Phys. Rev. Lett. 112, 128304.Google Scholar
Masoud, H. & Stone, H. A. 2014 A reciprocal theorem for Marangoni propulsion. J. Fluid Mech. 741, R4.Google Scholar
Morthomas, J. & Würger, A. 2010 Hydrodynamic attraction of immobile particles due to interfacial forces. Phys. Rev. E 81, 051405.CrossRefGoogle ScholarPubMed
Nagai, K. H., Takabatake, F., Sumino, Y., Kitahata, H., Ichikawa, M. & Yoshinaga, N. 2013 Rotational motion of a droplet induced by interfacial tension. Phys. Rev. E 87, 013009.Google Scholar
Nakata, S., Iguchi, Y., Ose, S., Kuboyama, M., Ishii, T. & Yoshikawa, K. 1997 Self-rotation of a camphor scraping on water: new insight into the old problem. Langmuir 13, 4454–4458.CrossRefGoogle Scholar
Okawa, D., Pastine, S. J., Zettl, A. & Fréchet, J. M. J. 2009 Surface tension mediated conversion of light to work. J. Am. Chem. Soc. 1 (31), 5396–5398.Google Scholar
Paxton, W. F., Sen, A. & Mallouk, T. E. 2005 Motility of catalytic nanoparticles through self-generated forces. Chem. Eur. J. 11, 6462–6470.Google Scholar
Qian, B., Montiel, D., Bregulla, A., Cichos, F. & Yang, H. 2013 Harnessing thermal fluctuations for purposeful activities: the manipulation of single micro-swimmers by adaptive photon nudging. Chem. Sci. 4, 1420–1429.Google Scholar
Robert de Saint Vincent, M. & Delville, J.-P. 2012 Microfluidic transport driven by opto-thermal effects. In Advances in Microfluidics (ed. Kelly, R. T.). InTech.Google Scholar
Schmitz, R. & Felderhof, B. U. 1982 Physica 113A, 90–102.CrossRefGoogle Scholar
Soh, S., Bishop, K. J. M. & Grzybowski, B. A. 2008 Dynamic self-assembly in ensembles of camphor boats. J. Phys. Chem. B 112, 10848–10853.CrossRefGoogle ScholarPubMed
Venancio-Marques, A., Barbaud, F. & Baigl, D. 2013 Microfluidic mixing triggered by an external LED illumination. J. Am. Chem. Soc. 135, 3218–3223.CrossRefGoogle ScholarPubMed