Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T14:54:26.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermal boundary-layer structure in laminar horizontal convection

Published online by Cambridge University Press:  31 March 2021

Bo Yan Open the ORCID record for Bo Yan [Opens in a new window] ,
Olga Shishkina Open the ORCID record for Olga Shishkina [Opens in a new window]  and
Xiaozhou He Open the ORCID record for Xiaozhou He [Opens in a new window]
Bo Yan
Affiliation:
School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen, 518055 China
Olga Shishkina
Affiliation:
Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077Göttingen, Germany
Xiaozhou He*
Affiliation:
School of Mechanical Engineering and Automation, Harbin Institute of Technology, Shenzhen, 518055 China Max Planck Institute for Dynamics and Self-Organization (MPIDS), 37077Göttingen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

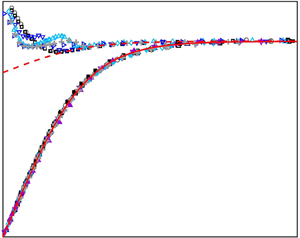
We present experimentally obtained time-averaged vertical temperature profiles $\theta (z)$ in horizontal convection (HC) in water (Prandtl number $Pr \simeq 6$), which were measured near the heating and cooling plates that are embedded in the bottom of HC samples. Three HC rectangular samples of different sizes but the same aspect ratio $\varGamma \equiv L:W:H = 10:1:1$ ($L$, $W$ and $H$ are the length, width and height of the sample, respectively) were used in the experiments, which allowed us to study HC in a Rayleigh-number range $2 \times 10^{10} \lesssim {Ra} \lesssim 9 \times 10^{12}$. The measurements revealed that above the cooling plate, the mean temperature profiles have a universal scaling form $\theta (z/\lambda _c)$ with $\lambda _c$ being a $Ra$-dependent thickness of the cold thermal boundary layer (BL). The $\theta (z/\lambda _c)$-profiles agree well with solutions to a laminar BL equation in HC, which is derived under assumption that the large-scale horizontal velocity achieves its maximum near the plate and vanishes in the bulk. Above the heating plate, the mean temperature field has a double-layer structure: in the lower layer, the $\theta$ profiles scale with the hot thermal BL thickness $\lambda _h$, while in the upper layer, they again scale with $\lambda _c$. Both scaling forms are in good agreement with the solutions to the BL equation with a proper parameter choice.

JFM classification

Boundary Layers: Boundary layer structure
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , R5
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–538.CrossRefGoogle Scholar
Ching, E.S.C., Dung, O.-Y. & Shishkina, O. 2017 Fluctuating thermal boundary layers and heat transfer in turbulent Rayleigh–Bénard convection. J. Stat. Phys. 167, 626–635.CrossRefGoogle Scholar
Ching, E.S.C., Leung, H.S., Zwirner, L. & Shishkina, O. 2019 Velocity and thermal boundary layer equations for turbulent Rayleigh–Bénard convection. Phys. Rev. Res. 1, 033037.CrossRefGoogle Scholar
Chiu-Webster, S., Hinch, E.J. & Liter, J.R. 2008 Very viscous horizontal convection. J. Fluid Mech. 611, 395–426.CrossRefGoogle Scholar
Estrada, F., Botzen, W.J.W. & Tol, R.S.J. 2011 A global economic assessment of city policies to reduce climate change impacts. Nat. Clim. Change 23, 025106.Google Scholar
Gramberg, H.J.J., Howell, P.D. & Ockendon, J.R. 2007 Convection by a horizontal thermal gradient. J. Fluid Mech. 586, 41–57.CrossRefGoogle Scholar
Griffiths, R.W., Hughes, G.O. & Gayen, B. 2013 Horizontal convection dynamics: insights from transient adjustment. J. Fluid Mech. 76, 559–595.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
He, X., Bodenschatz, E. & Ahlers, G. 2021 A model for universal spatial variations of temperature fluctuations in turbulent Rayleigh–Bénard convection. Theor. Appl. Mech. Lett. 11, 1.Google Scholar
He, X., Ching, E.S.C. & Tong, P. 2011 Locally-averaged thermal dissipation rate in turbulent thermal convection: a decomposition into contributions from different temperature gradient components. Phys. Fluids 23, 025106.CrossRefGoogle Scholar
He, X. & Tong, P. 2009 Measurements of the thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. E 79, 026306.CrossRefGoogle ScholarPubMed
Hughes, G.O. & Griffiths, R.W. 2008 Horizontal convection. Annu. Rev. Fluid Mech. 40 (1), 185–208.CrossRefGoogle Scholar
Kraichnan, R.H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Mullarney, J.C., Griffiths, R.W. & Hughes, G.O. 2004 Convection driven by differential heating at a horizontal boundary. J. Fluid Mech. 516, 181–209.CrossRefGoogle Scholar
Passaggia, P.-Y., Hurley, M.W., White, B. & Scotti, A. 2017 a Turbulent horizontal convection at high Schmidt numbers. Phys. Rev. Fluids 2, 090506.CrossRefGoogle Scholar
Passaggia, P.-Y., Scotti, A. & White, B. 2017 b Transition and turbulence in horizontal convection: linear stability analysis. J. Fluid Mech. 821, 31–58.CrossRefGoogle Scholar
Ramme, L. & Hansen, U. 2019 Transition to time-dependent flow in highly viscous horizontal convection. Phys. Rev. Fluids 4, 093501.CrossRefGoogle Scholar
Reiter, P. & Shishkina, O. 2020 Classical and symmetrical horizontal convection: detaching plumes and oscillations. J. Fluid Mech. 892, R1.CrossRefGoogle Scholar
Rossby, H.T. 1965 On thermal convection driven by non-uniform heating from below: an experimental study. Deep Sea Res. 12, 9–16.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
Scotti, A. & White, B. 2011 Is horizontal convection really ‘non-turbulent?’ Geophys. Res. Lett. 38, L21609.CrossRefGoogle Scholar
Sheard, G.J. & King, M.P. 2011 Horizontal convection: effect of aspect ratio on Rayleigh number scaling and stability. Appl. Math. Model. 35, 1647–1655.CrossRefGoogle Scholar
Shishkina, O. 2017 Mean flow structure in horizontal convection. J. Fluid Mech. 812, 525–540.CrossRefGoogle Scholar
Shishkina, O., Grossmann, S. & Lohse, D. 2016 Heat and momentum transport scalings in horizontal convection. Geophys. Res. Lett. 43 (3), 1219–1225.CrossRefGoogle Scholar
Shishkina, O., Horn, S., Emran, M.S. & Ching, E.S.C. 2017 Mean temperature profiles in turbulent thermal convection. Phys. Rev. Fluids 2, 113502.CrossRefGoogle Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E.S.C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114, 114302.CrossRefGoogle ScholarPubMed
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.CrossRefGoogle Scholar
Shishkina, O. & Wagner, S. 2016 Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett. 116, 024302.CrossRefGoogle ScholarPubMed
Shraiman, B.I. & Siggia, E.D. 1990 Heat transport in high-Rayleigh number convection. Phys. Rev. A 42, 3650–3653.CrossRefGoogle ScholarPubMed
Spiegel, E.A. 1971 Convection in stars. Annu. Rev. Astron. Astrophys. 9, 323–352.CrossRefGoogle Scholar
Tsai, T., Hussam, W.K., King, M.P. & Sheard, G.J. 2020 Transitions and scaling in horizontal convection driven by different temperature profiles. Intl J. Therm. Sci. 148, 106166.CrossRefGoogle Scholar
Wang, F., Huang, S. & Xia, K. 2018 Contribution of surface thermal forcing to mixing in the ocean. J. Geophys. Res. 123 (2), 855–863.CrossRefGoogle Scholar
Wang, F., Huang, S., Zhou, S. & Xia, K. 2016 Laboratory simulation of the geothermal heating effects on ocean overturning circulation. J. Geophys. Res. 121 (10), 7589–7598.CrossRefGoogle Scholar
Wang, Q., Lohse, D. & Shishkina, O. 2021 Scaling in internally heated convection: a unifying theory. Geophys. Res. Lett. 48, e2020GL091198.Google Scholar
Wang, W. & Huang, R.X. 2005 An experimental study on thermal circulation driven by horizontal differential heating. J. Fluid Mech. 540, 49–73.CrossRefGoogle Scholar
Wang, Y., He, X. & Tong, P. 2016 Boundary layer fluctuations and their effects on mean and variance temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Fluids 1, 082301(R).CrossRefGoogle Scholar
Wang, Y., Xu, W., He, X., Yik, H., Wang, X., Schumacher, J. & Tong, P. 2018 Boundary layer fluctuations in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 840, 408–431.CrossRefGoogle Scholar
Xu, W., Wang, Y., He, X., Wang, X., Schumacher, J., Huang, S. & Tong, P. 2021 Mean velocity and temperature profiles in turbulent Rayleigh–Bénard convection at low Prandtl numbers. J. Fluid Mech. (in press).Google Scholar