Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T17:00:09.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory of homogeneous vapour condensation and surface deposition from boundary layers

Published online by Cambridge University Press:  06 July 2012

M. D. Camejo  and
L. L. Bonilla
M. D. Camejo
Affiliation:
G. Millán Institute of Fluid Dynamics, Nanoscience and Industrial Mathematics, Universidad Carlos III de Madrid, 28911 Leganés, Spain
L. L. Bonilla*
Affiliation:
G. Millán Institute of Fluid Dynamics, Nanoscience and Industrial Mathematics, Universidad Carlos III de Madrid, 28911 Leganés, Spain School of Engineering and Applied Sciences. Harvard University, 29 Oxford Street, Cambridge, MA 02138, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Homogeneous condensation of vapours mixed with a carrier gas in the stagnation point boundary layer flow near a cold wall is considered. There is a condensation region near the wall with supersaturated vapour. Assuming that the surface tension times the molecular area is much larger than the thermal energy far from the wall, droplets are nucleated exclusively in a narrow nucleation layer where the Zeldovich flux of clusters surpassing the critical nucleus size is at a maximum. The vapour condenses in the free molecular regime on the droplets, which are thermophoretically attracted to the wall. Unlike the narrow condensation region for heterogeneous condensation on solid particles, in the case of homogeneous condensation the condensation region is wide even when the rate of vapour scavenging by droplets is large. A singular perturbation theory of homogeneous vapour condensation in boundary layer flow approximates very well the vapour and droplet density profiles, the nucleation layer and the deposition rates at the wall for wide ranges of the wall temperature and the scavenging parameter 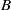. A key point in the theory is to select a trial vapour number density profile among a one parameter family of profiles between an upper and a lower bound. The maximum of the Zeldovich flux for supercritical nuclei provides the approximate location of the nucleation layer and an approximate droplet density profile. Then the condensate number of molecules and the vapour density profile are calculated by matched asymptotic expansions that also yield the deposition rates. For sufficiently large wall temperatures, a more precise corrected asymptotic theory is given.

JFM classification

Boundary Layers: Boundary layer structure Phase change: Condensation/evaporation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 706 , 10 September 2012 , pp. 534 - 559
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Castillo, J. L. & Rosner, D. E. 1988 A nonequilibrium theory of surface deposition from particle-laden, dilute condensible vapour-containing laminar boundary layers. Intl J. Multiphase Flow 14, 99–120.CrossRefGoogle Scholar
2. Castillo, J. L. & Rosner, D. E. 1989 Theory of surface deposition from a unary dilute vapour-containing steam, allowing for condensation within the laminar boundary layer. Chem. Engng Sci. 44, 925–937.CrossRefGoogle Scholar
3. Davis, E. J. 1983 Transport phenomena with single aerosol particles. Aerosol Sci. Technol. 2, 121–144.CrossRefGoogle Scholar
4. Delale, C. F. & Crighton, D. G. 1998 Prandtl–Meyer flows with homogeneous condensation. Part 1. Subcritical flows. J. Fluid Mech. 359, 23–47.CrossRefGoogle Scholar
5. Filippov, A. V. 2003 Simultaneous particle and vapour deposition in a laminar boundary layer. J. Colloid Interface Sci. 257, 2–12.CrossRefGoogle Scholar
6. Friedlander, S. K. 2000 Smoke, dust and haze. In Fundamentals of Aerosol Dynamics, 2nd edn. Oxford University Press.Google Scholar
7. García Ybarra, P. L. & Castillo, J. L. 1997 Mass transfer dominated by thermal diffusion in laminar boundary layers. J. Fluid Mech. 336, 379–409.CrossRefGoogle Scholar
8. Gökoglu, S. A. & Rosner, D. E. 1986 Thermophoretically augmented mass transfer rates to solid walls across laminar boundary layers. AIAA J. 24, 172–179.CrossRefGoogle Scholar
9. Jacobson, M. Z. 1996 Development and application of a new air pollution modelling system. Part 1. Atmos. Environ. 30, 1939–1963.CrossRefGoogle Scholar
10. Luo, X. S., Lamanna, G., Holten, A. P. C. & van Dongen, M. E. H. 2007 Effects of homogeneous condensation in compressible flows: Ludwieg-tube experiments and simulations. J. Fluid Mech. 572, 339–366.CrossRefGoogle Scholar
11. Neu, J. C., Bonilla, L. L. & Carpio, A. 2009 Theory of surface deposition from boundary layers containing condensable vapour and particles. J. Fluid Mech. 626, 183–210.CrossRefGoogle Scholar
12. Nowakowski, B. & Ruckenstein, E. 1991 A kinetic approach to the theory of nucleation in gases. J. Chem. Phys. 94, 1397–1402.CrossRefGoogle Scholar
13. Paoli, R., Helie, J. & Poinsot, T. 2004 Contrail formation in aircraft wakes. J. Fluid Mech. 502, 361–373.CrossRefGoogle Scholar
14. Peeters, P., Luijten, C. C. M. & van Dongen, M. E. H. 2001 Transport phenomena with single aerosol particles. Intl J. Heat Mass Transfer 44, 181–193.CrossRefGoogle Scholar
15. Pruppacher, H. R. & Klett, J. D. 1997 Microphysics of Clouds and Precipitation. Kluwer.Google Scholar
16. Pyykönen, J. & Jokiniemi, J. 2003 Modelling alkali chloride superheater deposition and its implications. Fuel Process. Technol. 80, 225–262.CrossRefGoogle Scholar
17. Rosner, D. E. 2000 Transport Processes in Chemically Reacting Flow Systems. Dover.Google Scholar
18. Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory, 8th edn. Springer.CrossRefGoogle Scholar
19. Sinha, S., Wyslouzil, B. E. & Wilemski, G. 2009 Modelling of condensation in supersonic nozzles. Aerosol Sci. Technol. 43, 9–24.Google Scholar
20. Tandon, P. & Murtagh, M. 2005 Particle–vapour interaction in deposition systems: influence on deposit morphology. Chem. Engng Sci. 60, 1685–1699.CrossRefGoogle Scholar
21. Wu, D. T. 1997 Nucleation theory. Solid State Phys. 50, 37–187.CrossRefGoogle Scholar
22. Zheng, F. 2002 Thermophoresis of spherical and non-spherical particles: a review of theories and experiments. Adv. Colloid Interface Sci. 97, 253–276.CrossRefGoogle ScholarPubMed