Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T12:49:43.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 1. ‘Long-wave’ regimes

Published online by Cambridge University Press:  23 January 2019

Alexander L. Frenkel ,
David Halpern Open the ORCID record for David Halpern [Opens in a new window]  and
Adam J. Schweiger
Alexander L. Frenkel
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
David Halpern*
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
Adam J. Schweiger
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A linear stability analysis of a two-layer plane Couette flow of two immiscible fluid layers with different densities, viscosities and thicknesses, bounded by two infinite parallel plates moving at a constant relative velocity to each other, with an insoluble surfactant monolayer along the interface and in the presence of gravity is carried out. The normal modes approach is applied to the equations governing flow disturbances in the two layers. These equations, together with boundary conditions at the plates and the interface, yield a linear eigenvalue problem. When inertia is neglected the velocity amplitudes are the linear combinations of certain hyperbolic functions, and a quadratic dispersion equation for the increment, that is the complex growth rate, is obtained, where coefficients depend on the aspect ratio, the viscosity ratio, the basic velocity shear, the Marangoni number 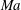$Ma$ that measures the effects of surfactant and the Bond number 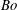$Bo$ that measures the influence of gravity. An extensive investigation is carried out that examines the stabilizing or destabilizing influences of these parameters. Since the dispersion equation is quadratic in the growth rate, there are two continuous branches of the normal modes: a robust branch that exists even with no surfactant, and a surfactant branch that, to the contrary, vanishes when 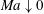$Ma\downarrow 0$. Regimes have been uncovered with crossings of the two dispersion curves, their reconnections at the point of crossing and separations as 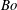$Bo$ changes. Due to the availability of the explicit forms for the growth rates, in many instances the numerical results are corroborated with analytical asymptotics.

JFM classification

Instability: Instability Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 150 - 184
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anshus, B. E. & Acrivos, A. 1967 The effect of surface active agents on the stability characteristics of falling liquid films. Chem. Engng Sci. 22, 389–393.10.1016/0009-2509(67)80126-XGoogle Scholar
Bak, J. & Newman, D. J. 2010 Complex Analysis. Springer.10.1007/978-1-4419-7288-0Google Scholar
Bassom, A. P., Blyth, M. G. & Papageorgiou, D. T. 2010 Nonlinear development of two-layer Couette–Poiseuille flow in the presence of surfactant. Phys. Fluids 22 (10), 102102.10.1063/1.3488226Google Scholar
Bassom, A. P., Blyth, M. G. & Papageorgiou, D. T. 2012 Using surfactants to stabilize two-phase pipe flows of core-annular type. J. Fluid Mech. 704, 333–359.10.1017/jfm.2012.243Google Scholar
Blyth, M. G. & Pozrikidis, C. 2004a Effect of inertia on the Marangoni instability of two-layer channel flow, Part II: normal-mode analysis. J. Engng Maths 50 (2–3), 329–341.10.1007/s10665-004-3691-zGoogle Scholar
Blyth, M. G. & Pozrikidis, C. 2004b Effect of surfactants on the stability of two-layer channel flow. J. Fluid Mech. 505, 59–86.10.1017/S0022112003007821Google Scholar
De Wit, A., Gallez, D. & Christov, C. I. 1994 Nonlinear evolution equations for thin liquid films with insoluble surfactants. Phys. Fluids 6, 3256–3266.10.1063/1.868058Google Scholar
Edwards, D. A., Brenner, H. & Wasan, D. T. 1991 Interfacial Tranport Processes and Rheology. Butterworth-Heinemann.Google Scholar
Frenkel, A. L. & Halpern, D. 2002 Stokes-flow instability due to interfacial surfactant. Phys. Fluids 14 (7), L45–L48.10.1063/1.1483838Google Scholar
Frenkel, A. L. & Halpern, D. 2005 Effect of inertia on the insoluble-surfactant instability of a shear flow. Phys. Rev. E 71 (1), 016302.Google Scholar
Frenkel, A. L. & Halpern, D. 2006 Strongly nonlinear nature of interfacial-surfactant instability of Couette flow. Intl J. Pure Appl. Maths 29 (2), 205–224.Google Scholar
Frenkel, A. L. & Halpern, D. 2017 Surfactant and gravity dependent instability of two-layer Couette flows and its nonlinear saturation. J. Fluid Mech. 826, 158–204.10.1017/jfm.2017.423Google Scholar
Frenkel, A. L., Halpern, D. & Schweiger, A. J.2018 Surfactant and gravity dependent instability of two-layer channel flows: linear theory covering all wave lengths, arXiv:1801.09290.Google Scholar
Frenkel, A. L., Halpern, D. & Schweiger, A. J. 2019 Surfactant- and gravity-dependent instability of two-layer channel flows: linear theory covering all wavelengths. Part 2. Mid-wave regimes. J. Fluid Mech. 863, 185–214.10.1017/jfm.2018.991Google Scholar
Halpern, D. & Frenkel, A. L. 2003 Destabilization of a creeping flow by interfacial surfactant: Linear theory extended to all wavenumbers. J. Fluid Mech. 485, 191–220.10.1017/S0022112003004476Google Scholar
Hesla, T. I., Prankch, F. R. & Preziosi, L. 1986 Squire’s theorem for two stratified fluids. Phys. Fluids 29, 2808–2811.10.1063/1.865478Google Scholar
Joseph, D. D. & Renardy, Y. 1993 Fundamentals of Two-Fluid Dynamics, vol I: Mathematical Theory and Applications; vol II: Lubricated Transport, Drops and Miscible Liquids. Springer.Google Scholar
Kalogirou, A. 2018 Instability of two-layer film flows due to the interacting effects of surfactants, inertia, and gravity. Phys. Fluids 30 (3), 030707.Google Scholar
Kalogirou, A. & Papageorgiou, D. T. 2016 Nonlinear dynamics of surfactant-laden two-fluid Couette flows in the presence of inertia. J. Fluid Mech. 802, 5–36.10.1017/jfm.2016.429Google Scholar
Kalogirou, A., Papageorgiou, D. T. & Smyrlis, Y.-S. 2012 Surfactant destabilization and non-linear phenomena in two-fluid shear flows at small Reynolds numbers. IMA J. Appl. Maths 77 (3), 351–360.10.1093/imamat/hxs035Google Scholar
Kwak, S. & Pozrikidis, C. 2001 Effect of surfactants on the instability of a liquid thread or annular layer. Part I: Quiescent fluids. Intl J. Multiphase Flow 27, 1–37.10.1016/S0301-9322(00)00011-2Google Scholar
Otis, D. R., Johnson, M., Pedley, T. J. & Kamm, R. D. 1993 Role of pulmonary surfactant in airway closure: a computational study. J. Appl. Phys. 75, 1323–1333.Google Scholar
Picardo, J. R., Radhakrishna, T. G. & Pushpavanam, S. 2016 Solutal Marangoni instability in layered two-phase flows. J. Fluid Mech. 793, 280–315.10.1017/jfm.2016.135Google Scholar
Pozrikidis, C. 2004 Effect of inertia on the Marangoni instability of two-layer channel flow. Part I: numerical simulations. J. Engng Maths 50 (2–3), 311–327.10.1007/s10665-004-3690-0Google Scholar
Pozrikidis, C. & Hill, A. I. 2011 Surfactant-induced instability of a sheared liquid layer. IMA J. Appl. Maths 76 (6), 859–875.10.1093/imamat/hxq067Google Scholar
Rickett, L. M., Penfold, R., Blyth, M. G., Purvis, R. & Cooker, M. J. 2015 Incipient mixing by Marangoni effects in slow viscous flow of two immiscible fluid layers. IMA J. Appl. Maths 80 (5), 1582–1618.10.1093/imamat/hxv009Google Scholar
Schweiger, A. J.2013 Gravity, surfactants, and instabilities of two-layer shear flows. PhD thesis, The University of Alabama.Google Scholar
Sternling, C. V. & Scriven, L. E. 1959 Interfacial turbulence: hydrodynamic instability and the Marangoni effect. AIChE J. 5 (4), 514–523.10.1002/aic.690050421Google Scholar
Wei, H. H. 2005 On the flow-induced Marangoni instability due to the presence of surfactant. J. Fluid Mech. 544, 173–200.10.1017/S0022112005006609Google Scholar
Whitaker, S. 1964 Effect of surface active agents on the stability of falling liquid films. Ind. Engng Chem. Fundam. 3, 132–142.10.1021/i160010a009Google Scholar
Wong, H., Rumschitzki, D. & Maldarelli, C. 1996 On the surfactant mass balance at a deforming fluid interface. Phys. Fluids 8, 3203–3204.10.1063/1.869098Google Scholar
Yih, C. S. 1967 Instability due to viscosity stratification. J. Fluid Mech. 27, 337–352.10.1017/S0022112067000357Google Scholar