Spanwise wall oscillation has been extensively studied to explore possible drag control methods, mechanisms and efficacy – particularly for incompressible flows. We performed direct numerical simulation for fully developed turbulent channel flow to establish how effective spanwise wall oscillation is when the flow is compressible and also to document its drag reduction (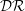${\mathcal{D}}{\mathcal{R}}$) trend with Mach number. Drag reduction 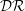${\mathcal{D}}{\mathcal{R}}$ is first investigated for three different bulk Mach numbers 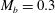$M_{b}=0.3$, 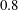$0.8$ and 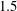$1.5$ at a fixed bulk Reynolds number 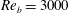$Re_{b}=3000$. At a given velocity amplitude 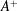$A^{+}$ (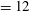$=12$), 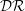${\mathcal{D}}{\mathcal{R}}$ at 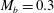$M_{b}=0.3$ agrees with the strictly incompressible case; at 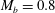$M_{b}=0.8$, 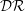${\mathcal{D}}{\mathcal{R}}$ exhibits a similar trend to that at 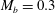$M_{b}=0.3$: 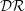${\mathcal{D}}{\mathcal{R}}$ increases with the oscillation period 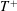$T^{+}$ to a maximum and then decreases gradually. However, at 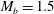$M_{b}=1.5$, 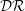${\mathcal{D}}{\mathcal{R}}$ monotonically increases with 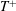$T^{+}$. In addition, the maximum 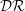${\mathcal{D}}{\mathcal{R}}$ is found to increase with 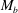$M_{b}$. For 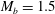$M_{b}=1.5$, similar to the incompressible case, 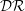${\mathcal{D}}{\mathcal{R}}$ increases with 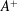$A^{+}$, but the rate of increase decreases at larger 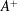$A^{+}$. Unlike the flow behaviour when incompressible, the flow surprisingly relaminarizes when it is supersonic (at 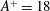$A^{+}=18$ and 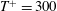$T^{+}=300$) – this enigmatic behaviour requires further detailed studies for different domain sizes, 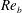$Re_{b}$ and 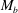$M_{b}$. The Reynolds number effect on 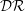${\mathcal{D}}{\mathcal{R}}$ is also investigated. Although 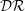${\mathcal{D}}{\mathcal{R}}$ generally decreases with 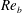$Re_{b}$, it is less affected at small $T^{+}$, but drops rapidly at large 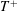$T^{+}$. We introduce a simple scaling for the oscillation period as 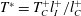$T^{\ast }=T_{C}^{+}l_{I}^{+}/l_{C}^{+}$, with 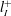$l_{I}^{+}$ and 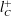$l_{C}^{+}$ denoting the mean streak spacing for incompressible and compressible cases, respectively. At the same semi-local Reynolds number 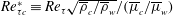$Re_{\unicode[STIX]{x1D70F}c}^{\ast }\equiv Re_{\unicode[STIX]{x1D70F}}\sqrt{\overline{\unicode[STIX]{x1D70C}}_{c}/\overline{\unicode[STIX]{x1D70C}}_{w}}/(\overline{\unicode[STIX]{x1D707}}_{c}/\overline{\unicode[STIX]{x1D707}}_{w})$ (subscripts $c$ and 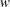$w$ denote quantities at the channel centre and wall, respectively), ${\mathcal{D}}{\mathcal{R}}$ as a function of 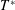$T^{\ast }$ exhibits good agreement between the supersonic and strictly incompressible cases, with the optimal oscillation period becoming 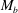$M_{b}$-invariant as 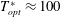$T_{opt}^{\ast }\approx 100$.