Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T13:30:15.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Supersonic flow around a cylinder with a permeable high-porosity insert: experiment and numerical simulation

Published online by Cambridge University Press:  26 March 2019

Anatoly A. Maslov Open the ORCID record for Anatoly A. Maslov [Opens in a new window] ,
S. G. Mironov Open the ORCID record for S. G. Mironov [Opens in a new window] ,
T. V. Poplavskaya Open the ORCID record for T. V. Poplavskaya [Opens in a new window]  and
S. V. Kirilovskiy Open the ORCID record for S. V. Kirilovskiy [Opens in a new window]
Anatoly A. Maslov*
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, Siberian Branch, Russian Academy of Sciences, Novosibirsk 630090, Russia
S. G. Mironov
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, Siberian Branch, Russian Academy of Sciences, Novosibirsk 630090, Russia
T. V. Poplavskaya
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, Siberian Branch, Russian Academy of Sciences, Novosibirsk 630090, Russia
S. V. Kirilovskiy
Affiliation:
Khristianovich Institute of Theoretical and Applied Mechanics, Siberian Branch, Russian Academy of Sciences, Novosibirsk 630090, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

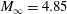Results of experimental and numerical investigations of a supersonic flow around a cylinder with a frontal gas-permeable insert made of a high-porosity cellular material are presented. The measurements are performed in a T-327 supersonic blowdown wind tunnel at the free-stream Mach numbers $M_{\infty }=4.85$, 7 and 21 in the range of the unit Reynolds numbers 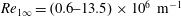$Re_{1\infty }=(0.6{-}13.5)\times 10^{6}~\text{m}^{-1}$. The drag coefficients for a cylinder with an aerospike and a cylinder with a frontal gas-permeable porous insert are obtained. For the cylinder with the frontal gas-permeable porous insert, variations of the insert length, cylinder diameter and pore size are considered, and the mechanism of drag reduction is found, which includes two supplementary processes: attenuation of the bow shock wave in a system of weaker shock waves, and formation of an effective pointed body. The experiments are accompanied by numerical simulations of the flow around the cylinder with the frontal high-porosity insert: the fields of parameters of the external flow and the flow inside the porous insert are obtained, the drag coefficients are calculated, and the shape of the effective body for the examined model is found. The structure of the high-porosity material is modelled by a system of staggered rings of different diameters aligned in the radial and longitudinal directions (skeleton model of a porous medium). Numerical simulations of the problem are performed by means of solving two-dimensional Reynolds-averaged Navier–Stokes equations written in an axisymmetric form. The experimental and numerical data reveal significant drag reduction in a wide range of supersonic flow conditions. The results obtained on the drag coefficient for the cylinder are generalized with the use of a parameter which includes the ratio of the cylinder diameter to the pore diameter in the insert and the Mach number. This parameter is proposed as a similarity criterion for the problem of a supersonic flow around a cylinder with a frontal high-porosity insert.

JFM classification

Flow Control: Drag reduction Compressible Flows: Gas dynamics Aerodynamics: High-speed flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 611 - 632
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bauer, S. X. S. & Hemsch, M. J. 1994 Allevation of side force on tangent-ogive forebodies using passive porosity. J. Aircraft 31 (2), 354–361.Google Scholar
Bauer, S. X. S. & Hernandez, G.1988 Reduction of cross-flow shock-induced separation with a porous cavity at supersonic speeds. AIAA Paper 1988-2567.Google Scholar
Bedarev, I. A., Mironov, S. G., Serdyuk, K. M., Fedorov, A. V. & Fomin, V. M. 2011 Physical and mathematical modeling of a supersonic flow around a cylinder with a porous insert. J. Appl. Mech. Tech. Phys. 52 (1), 9–17.Google Scholar
Belov, S. V. 1987 Porous Permeable Materials–Handbook (ed. Belov, S. V.), p. 335. Metallurgiya.Google Scholar
Daum, F. L. & Gyarmathy, G. 1968 Condensation of air and nitrogen in hypersonic wind tunnels. AIAA J. 6 (3), 458–465.Google Scholar
Fedorov, A. V., Malmuth, N. D., Rasheed, A. & Hornung, H. G. 2001 Stabilization of hypersonic boundary layer by porous coatings. AIAA J. 34 (3), 605–610.Google Scholar
Fedorov, A. V., Shiplyuk, A. N., Maslov, A. A., Burov, E. V. & Malmuth, N. D. 2003 Stabilization of hypersonic boundary layer using an ultrasonically absorptive coating. J. Fluid Mech. 479, 99–124.Google Scholar
Fomin, V. M., Mironov, S. G. & Serdyuk, K. M. 2009a Reducing the wave drag of bodies in supersonic flows using porous materials. Tech. Phys. Lett. 35 (3), 117–119.Google Scholar
Fomin, V. M. & Postnikov, B. V. 2015 Changing the regime of supersonic flow past a rectangular step using gas-permeable inserts. Tech. Phys. Lett. 49 (9), 686–688.Google Scholar
Fomin, V. M., Zapryagaev, V. I., Lokotko, A. V. & Volkov, V. F. 2009b Effect of gas-permeable surface areas on aerodynamic characteristics of a body of rotation at supersonic velocities. Dokl. Phys. 54 (8), 383–388.Google Scholar
Fomin, V. M., Zapryagaev, V. I., Lokotko, A. V., Volkov, V. F., Lutskii, A. E., Menshov, I. S., Maksimov, Y. M. & Kirdyashkin, A. I. 2010 Aerodynamic characteristics of a body of revolution with gas-permeable surface areas. J. Appl. Mech. Tech. Phys. 51 (1), 65–73.Google Scholar
Hartman, T. & Morgenstern, J. M.2004 Passive aerodynamic sonic boom suppression for supersonic aircraft. US Pat. 0065774 A1.Google Scholar
Hunter, C. A., Viken, S. A., Wood, R. M. & Bauer, S. X. S.2001 Advanced aerodynamic design of passive porosity control effectors. AIAA Paper 2001-0249.Google Scholar
Kirilovskiy, S. V., Maslov, A. A., Mironov, S. G. & Poplavskaya, T. V. 2018 Application of the skeleton model of a highly porous cellular material in modeling supersonic flow past a cylinder with a forward gas-permeable insert. Fluid Dyn. 53 (3), 409–4168.Google Scholar
Kirsanov, Y. A., Nazipov, R. A. & Danilov, V. A. 2011 Heat transfer between a porous body and a single-phase flow of the heat carrier. High Temp. 49 (2), 227–235.Google Scholar
Levi-Hevroni, D., Levy, A., Ben-Dor, G. & Sorec, S. 2002 Numerical investigation of the propagation of planar shock waves in saturated flexible porous materials: development of the computer code and comparison with experimental results. J. Fluid Mech. 462, 285–306.Google Scholar
Levi-Hevroni, D., Levy, A., Ben-Dor, G. & Sorec, S. 2006 The interaction of planar shock waves with multiphase saturated flexible porous materials – a numerical investigation. J. Fluid Mech. 563, 159–188.Google Scholar
Levy, A., Ben-Dor, G. & Sorec, S. 1996 Numerical investigation of the propagation of shock waves in rigid porous materials: development of the computer code and comparison with experimental results. J. Fluid Mech. 324, 163–179.Google Scholar
Maslov, A. A., Mironov, S. G., Poplavskaya, T. V., Tsyryulnikov, I. S. & Kirilovskiy, S. V. 2012 Effect of sound-absorbing materials on intensity of disturbances in the shock layer on a flat plate aligned at an angle of attack. J. Appl. Mech. Tech. Phys. 53 (2), 162–172.Google Scholar
Menter, F. R. 1994 Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 32 (8), 1598–1605.Google Scholar
Mironov, S. G., Maslov, A. A., Poplavskaya, T. V. & Kirilovskiy, S. V. 2015a Modeling of a supersonic flow around a cylinder with a gas-permeable porous insert. J. Appl. Mech. Tech. Phys. 56 (4), 549–557.Google Scholar
Mironov, S. G., Maslov, A. A. & Tsyryulnikov, I. S. 2014 Controlling aerodynamic forces with the aid of gas-permeable porous materials. Tech. Phys. Lett. 40 (10), 888–890.Google Scholar
Mironov, S. G., Maslov, A. A. & Tsyryulnikov, I. S.2015b Method of control of supersonic aircraft overflow. RU Pat. 2559193 C1.Google Scholar
Mironov, S. G., Poplavskaya, T. V. & Kirilovskiy, S. V. 2017 Impact of frontal-porous-insert temperature on the cylinder drag in supersonic flow. Thermophys. Aeromech. 24 (4), 629–632.Google Scholar
Mitrichev, I. I., Koltsova, E. M. & Zhensa, A. V. 2012 Computer simulation of gasdynamic conditions in channels of open-cell foam. Fundam. Res. Tech. Sci. 11 (2), 440–446.Google Scholar
Nagamatsu, H. T., Orozco, R. D. & Ling, D. C.1984 Porosity effect on supercritical airfoil drag reduction by shock wave/boundary layer control. AIAA Paper 1984-1682.Google Scholar
Ram, O. & Sadot, O. 2013 A simple constitutive model for predicting the pressure histories developed behind rigid porous media impinged by shock waves. J. Fluid Mech. 718, 507–523.Google Scholar
Richardson, L. F. 1927 The deferred approach to the limit. Proc. R. Soc. Lond. A 226, 299–361.Google Scholar
Roache, P. J. 1994 Perspective: a method for uniform reporting of grid refinement studies. Trans. ASME J. Fluids Engng 116, 405–413.Google Scholar
Sandham, N. D. & Ludeke, H. 2009 A numerical study of Mach 6 boundary layer stabilization by means of a porous surface. AIAA J. 47 (9), 2243–2252.Google Scholar
Tsyryulnikov, I. S., Maslov, A. A., Mironov, S. G., Poplavskaya, T. V. & Kirilovskiy, S. V. 2015 The efficiency of the method of sound-absorbing coatings in vibrationally excited hypersonic flow. Tech. Phys. Lett. 42 (1), 184–186.Google Scholar
Wartemann, V., Ludeke, H. & Sandham, N. D. 2012 Numerical investigation of hypersonic-boundary layer stabilization by porous surfaces. AIAA J. 50 (6), 1281–1290.Google Scholar
Zapryagaev, V. I. & Mironov, S. G. 1989 Experimental study of pulsations in the forward separation zone in a supersonic flow. J. Appl. Mech. Tech. Phys. 30 (4), 620–627.Google Scholar
Zapryagaev, V. I., Solotchin, V. I., Kavun, I. N. & Yarovoy, D. A. 2011 Impingement of a supersonic underexpanded jet onto obstacles with different permeabilities. J. Appl. Mech. Tech. Phys. 52 (5), 727–733.Google Scholar