Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-08T05:24:35.915Z Has data issue: false hasContentIssue false
  • English
  • Français

A study of singular modes associated with over-reflection and related phenomena

Published online by Cambridge University Press:  03 July 2013

S. A. Maslowe  and
R. J. Spiteri
S. A. Maslowe*
Affiliation:
Department of Mathematics, McGill University, Montreal, QC H3A 0B9, Canada
R. J. Spiteri
Affiliation:
Department of Computer Science, University of Saskatchewan, SK S7N 5C9, Canada
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper describes an investigation of the linear, diffusive critical layer for shear flows whose inviscid neutral modes have an algebraic branch point. As examples of flows exhibiting such singular behaviour, we treat both stratified shear flows and non-axisymmetric modes on vortices. For the stratified case, the coupled vorticity and energy equations are solved numerically. In this way, the density perturbation, which is unbounded in the absence of diffusion, is determined directly. As an example featuring a vortex, we consider helical modes on a modified Lamb–Oseen vortex whose velocity profile is perturbed in such a way that linear instability is possible. Both the axial and azimuthal velocity perturbations in the critical layer are determined. A characteristic shared by all the above problems is that they involve eigenfunctions that are oscillatory in some region. For forced waves in a stably stratified shear flow, we consider a larger range of parameters than previous investigators. We also examine some experiments and find that the Reynolds stress is sensitive to the actual density profile in the region between a wavy wall providing the forcing and the critical layer. For the stratified shear flows without forcing, much smaller Richardson numbers are involved and the modes considered are over-reflecting. For an unbounded 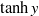$\tanh y$ mixing layer, we show that the Reynolds stress for a neutral mode must jump across the critical layer. With the presence of a horizontal boundary beneath the shear layer, on the other hand, over-reflection can occur, with the Reynolds stress vanishing on either side of the critical layer. In all cases, the variation of the Reynolds stress across the critical layer is determined.

JFM classification

Waves/Free-surface Flows: Critical layers Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , pp. 120 - 145
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
Baldwin, P. & Roberts, P. H. 1970 The critical layer in stratified shear flow. Mathematika 17, 513–539.CrossRefGoogle Scholar
Benilov, E. & Lapin, V. N. 2012 On resonant over-reflection of waves by jets. Geophys. Astrophys. Fluid Dyn. 107, 1–24.Google Scholar
Booker, J. R. & Bretherton, F. P. 1967 The critical layer for gravity waves in a shear flow. J. Fluid Mech. 27, 513–539.CrossRefGoogle Scholar
Caillol, P. & Maslowe, S. A. 2007 The nonlinear critical layer for Kelvin modes on a vortex. Stud. Appl. Maths 118, 221–254.CrossRefGoogle Scholar
Campbell, L. J. 2004 Wave-mean flow interactions in a forced Rossby wave packet critical layer. Stud. Appl. Maths 112, 39–85.CrossRefGoogle Scholar
Craik, A. D. D. 1985 Wave Interactions and Fluid Flows. Cambridge University Press.Google Scholar
Delisi, D. P. & Dunkerton, T. J. 1989 Laboratory observations of gravity wave critical-layer flows. Pure Appl. Geophys. 130, 445–461.CrossRefGoogle Scholar
Drazin, P. G. 1958 The stability of a shear layer in an unbounded heterogeneous inviscid fluid. J. Fluid Mech. 4, 214–224.CrossRefGoogle Scholar
Drazin, P. G., Zaturska, M. B. & Banks, W. H. H. 1979 On the normal modes of parallel flow of inviscid stratified fluid. Part 2. Unbounded flow with propagation at infinity. J. Fluid Mech. 95, 681–705.CrossRefGoogle Scholar
Eltayeb, I. A. & McKenzie, J. F. 1975 Critical-level behaviour and wave amplification of a gravity wave incident upon a shear layer. J. Fluid Mech. 72, 661–671.CrossRefGoogle Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.CrossRefGoogle Scholar
Gage, K. S. & Reid, W. H. 1968 The stability of thermally stratified plane Poiseuille flow. J. Fluid Mech. 33, 21–32.CrossRefGoogle Scholar
Galperin, B., Sukoriansky, S. & Anderson, P. S. 2007 On the critical Richardson number in stably stratified turbulence. Atmos. Sci. Lett. 8, 65–69.CrossRefGoogle Scholar
Hazel, P. 1967 The effect of viscosity and heat conduction on internal gravity waves at a critical level. J. Fluid Mech. 30, 775–783.CrossRefGoogle Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.CrossRefGoogle Scholar
Howard, L. N. & Gupta, A. S. 1962 On the hydrodynamic and hydromagnetic stability of swirling flows. J. Fluid Mech. 14, 463–476.CrossRefGoogle Scholar
Kierzenka, J. & Shampine, L. F. 2008 A BVP solver that controls residual and error. J. Numer. Anal. Ind. Appl. Maths 3, 27–41.Google Scholar
Koppel, D. 1964 On the stability of flow of a thermally stratified fluid under the action of gravity. J. Math. Phys. 5, 963–982.CrossRefGoogle Scholar
Lalas, D. P. & Einaudi, F. 1976 On the characteristics of gravity waves generated by atmospheric shear layers. J. Atmos. Sci. 33, 1248–1259.2.0.CO;2>CrossRefGoogle Scholar
Le Dizès, Stéphane 2004 Viscous critical-layer analysis of vortex normal modes. Stud. Appl. Maths 112, 315–332.CrossRefGoogle Scholar
Lessen, M, Singh, P. J. & Paillet, F. 1974 The stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63, 753–763.CrossRefGoogle Scholar
Lindzen, R. S. & Barker, J. W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.CrossRefGoogle Scholar
Maslowe, S. A. 1986 Critical layers in shear flows. Annu. Rev. Fluid Mech. 18, 405–432.CrossRefGoogle Scholar
Menkes, J. 1959 On the stability of a shear layer. J. Fluid Mech. 6, 518–522.CrossRefGoogle Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.CrossRefGoogle Scholar
Rosenthal, A. J. & Lindzen, R. S. 1983 Instabilities in a stratified fluid having one critical level. Part II. Explanation of gravity wave instabilities using the concept of overreflection. J. Atmos. Sci. 40, 521–529.2.0.CO;2>CrossRefGoogle Scholar
Spalart, Philippe. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30, 107–138.CrossRefGoogle Scholar
Stewartson, K. 1981 Marginally stable inviscid flows with critical layers. IMA J. Appl. Maths 27, 133–175.CrossRefGoogle Scholar
Stuart, J. T. 1963 Hydrodynamic stability. In Laminar Boundary Layers (ed. Rosenhead, L.), chap. 9. Oxford University Press.Google Scholar