Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T08:56:07.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure and stability of steady porous medium convection at large Rayleigh number

Published online by Cambridge University Press:  05 May 2015

Baole Wen ,
Lindsey T. Corson  and
Gregory P. Chini
Baole Wen
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH 03824, USA Center for Fluid Physics, University of New Hampshire, Durham, NH 03824, USA
Lindsey T. Corson
Affiliation:
Department of Mathematics and Statistics, University of Strathclyde, 26 Richmond Street, Glasgow G1 1XH, UK
Gregory P. Chini*
Affiliation:
Program in Integrated Applied Mathematics, University of New Hampshire, Durham, NH 03824, USA Center for Fluid Physics, University of New Hampshire, Durham, NH 03824, USA Department of Mechanical Engineering, University of New Hampshire, Durham, NH 03824, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A systematic investigation of unstable steady-state solutions of the Darcy–Oberbeck–Boussinesq equations at large values of the Rayleigh number 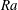$\mathit{Ra}$ is performed to gain insight into two-dimensional porous medium convection in domains of varying aspect ratio 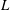$L$. The steady convective states are shown to transport less heat than the statistically steady ‘turbulent’ flow realised at the same parameter values: the Nusselt number 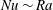$\mathit{Nu}\sim \mathit{Ra}$ for turbulent porous medium convection, while 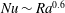$\mathit{Nu}\sim \mathit{Ra}^{0.6}$ for the maximum heat-transporting steady solutions. A key finding is that the lateral scale of the heat-flux-maximising solutions shrinks roughly as 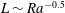$L\sim \mathit{Ra}^{-0.5}$, reminiscent of the decrease of the mean inter-plume spacing observed in turbulent porous medium convection as the thermal forcing is increased. A spatial Floquet analysis is performed to investigate the linear stability of the fully nonlinear steady convective states, extending a recent study by Hewitt et al. (J. Fluid Mech., vol. 737, 2013, pp. 205–231) by treating a base convective state, and secondary stability modes, that satisfy appropriate boundary conditions along plane parallel walls. As in that study, a bulk instability mode is found for sufficiently small-aspect-ratio base states. However, the growth rate of this bulk mode is shown to be significantly reduced by the presence of the walls. Beyond a certain critical 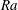$\mathit{Ra}$-dependent aspect ratio, the base state is most strongly unstable to a secondary mode that is localised near the heated and cooled walls. Direct numerical simulations, strategically initialised to investigate the fully nonlinear evolution of the most dangerous secondary instability modes, suggest that the (long time) mean inter-plume spacing in statistically steady porous medium convection results from a balance between the competing effects of these two types of instability.

JFM classification

Convection: Convection in porous media Instability: Instability Nonlinear Dynamical Systems: Pattern formation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 197 - 224
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aidun, C. K. & Steen, P. H. 1987 Transition to oscillatory convective heat transfer in a fluid-saturated porous medium. J. Thermophys. Heat Transfer 1, 268–273.Google Scholar
Bejan, A. 2013 Convection Heat Transfer, 4th edn. Wiley.Google Scholar
Boyd, J. P. 2000 Chebyshev and Fourier Spectral Methods, 2nd edn. Dover.Google Scholar
Busse, F. H. 1967 The stability of finite amplitude cellular convection and its relation to an extremum principle. J. Fluid Mech. 30, 625–649.CrossRefGoogle Scholar
Busse, F. H. 1972 The oscillatory instability of convection rolls in a low Prandtl number fluid. J. Fluid Mech. 52, 97–112.CrossRefGoogle Scholar
Chini, G. P., Julien, K. & Knobloch, E. 2009 An asymptotically reduced model of turbulent Langmuir circulation. Geophys. Astrophys. Fluid Dyn. 103, 179–197.CrossRefGoogle Scholar
Clever, R. M. & Busse, F. H. 1974 The oscillatory instability of convection rolls in a low Prandtl number fluid. J. Fluid Mech. 65, 625–645.Google Scholar
Corson, L. T. 2011 Maximizing the heat flux in steady unicellular porous media convection. In Geophysical Fluid Dynamics Program Report, Woods Hole Oceanographic Institution.Google Scholar
Elder, J. W. 1967 Steady free convection in a porous medium heated from below. J. Fluid Mech. 27, 29–48.CrossRefGoogle Scholar
Fowler, A. C. 1997 Mathematical Models in the Applied Sciences. Cambridge University Press.Google Scholar
Graham, M. D. & Steen, P. H. 1992 Strongly interacting traveling waves and quasiperiodic dynamics in porous medium convection. Physica D 54, 331–350.Google Scholar
Graham, M. D. & Steen, P. H. 1994 Plume formation and resonant bifurcations in porous-media convection. J. Fluid Mech. 272, 67–90.Google Scholar
Herbert, T. 1983 Secondary instability of plane channel flow to subharmonic three-dimensional disturbances. Phys. Fluids 26, 871–874.Google Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20, 487–526.CrossRefGoogle Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2012 Ultimate regime of high Rayleigh number convection in a porous medium. Phys. Rev. Lett. 108, 224503.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Stability of columnar convection in a porous medium. J. Fluid Mech. 737, 205–231.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2014 High Rayleigh number convection in a three-dimensional porous medium. J. Fluid Mech. 748, 879–895.CrossRefGoogle Scholar
Horne, R. N. & O’Sullivan, M. J. 1974 Oscillatory convection in a porous medium heated from below. J. Fluid Mech. 66, 339–352.Google Scholar
Horton, C. W. & Rogers, F. T. 1945 Convection currents in a porous medium. J. Appl. Phys. 16, 367–370.Google Scholar
Kelly, R. E. 1967 On the stability of an inviscid shear layer which is periodic in space and time. J. Fluid Mech. 27, 657–689.Google Scholar
Kimura, S., Schubert, G. & Straus, J. M. 1986 Route to chaos in porous-medium thermal convection. J. Fluid Mech. 166, 305–324.CrossRefGoogle Scholar
Kimura, S., Schubert, G. & Straus, J. M. 1987 Instabilities of steady, periodic, and quasi-periodic modes of convection in porous media. Trans. ASME J. Heat Transfer 109, 350–355.Google Scholar
Lapwood, E. R. 1948 Convection of a fluid in a porous medium. Proc. Camb. Phil. Soc. 44, 508–521.Google Scholar
Metz, B., Davidson, O., de Coninck, H., Loos, M. & Meyer, L. 2005 IPCC Special Report on Carbon Dioxide Capture and Storage. Cambridge University Press.Google Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media, 3rd edn. Springer.Google Scholar
Orszag, S. A. & Patera, A. T. 1983 Secondary instability of wall-bounded shear flows. J. Fluid Mech. 128, 347–385.CrossRefGoogle Scholar
Otero, J., Dontcheva, L. A., Johnston, H., Worthing, R. A., Kurganov, A., Petrova, G. & Doering, C. R. 2004 High-Rayleigh-number convection in a fluid-saturated porous layer. J. Fluid Mech. 500, 263–281.Google Scholar
Palm, E., Weber, J. E. & Kvernvold, O. 1972 On steady convection in a porous medium. J. Fluid Mech. 54, 153–161.Google Scholar
Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks. Cambridge University Press.Google Scholar
Phillips, O. M. 2009 Geological Fluid Dynamics: Sub-surface Flow and Reactions. Cambridge University Press.Google Scholar
Schubert, G. & Straus, J. M. 1982 Transitions in time-dependent thermal convection in fluid-saturated porous media. J. Fluid Mech. 121, 301–313.Google Scholar
Tandon, A. & Leibovich, S. 1995 Secondary instabilities in Langmuir circulations. J. Phys. Oceanogr. 25, 1206–1217.Google Scholar
Wen, B., Chini, G. P., Dianati, N. & Doering, C. R. 2013 Computational approaches to aspect-ratio-dependent upper bounds and heat flux in porous medium convection. Phys. Lett. A 377, 2931–2938.Google Scholar