Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T06:42:47.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Streamwise variation of turbulent dynamics in boundary layer flow of drag-reducing fluid

Published online by Cambridge University Press:  22 September 2011

Shinji Tamano ,
Michael D. Graham  and
Yohei Morinishi
Shinji Tamano*
Affiliation:
Graduate School of Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan Department of Chemical and Biological Engineering, University of Wisconsin–Madison, Madison, WI 53706-1607, USA
Michael D. Graham
Affiliation:
Department of Chemical and Biological Engineering, University of Wisconsin–Madison, Madison, WI 53706-1607, USA
Yohei Morinishi
Affiliation:
Graduate School of Engineering, Nagoya Institute of Technology, Gokiso-cho, Showa-ku, Nagoya, Aichi 466-8555, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNSs) of a zero-pressure-gradient boundary layer flow of a polymeric fluid have been performed. The FENE-P model was used for the polymer stresses and a wide range of Weissenberg numbers (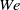) was addressed. In all cases, the streamwise variations of the level of polymer stretching and the level of drag reduction are anticorrelated. Consistent with earlier studies, the inlet condition for the flow consists of Newtonian velocity data with no polymer stretching, so in the upstream region of the boundary layer the polymer molecules stretch strongly in response, leading to an initial spatial maximum in polymer stretching. Beyond this initial region, the level of drag reduction increases with increasing downstream position, while the polymer stretch is decreasing. At sufficiently high Weissenberg numbers, these variations are monotonic with streamwise position (outside the upstream region), but at 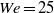, both the polymer stretching and level of drag reduction display a decaying oscillation in the downstream position. The streamwise dependence of the velocity statistics is also shown. In addition, simulations in which the polymer stress is turned off beyond a chosen downstream position were performed; in this case the flow continues to exhibit substantial drag reduction well downstream of the cutoff position. These observations are analysed in light of other recent literature and in particular the observations of ‘active’ and ‘hibernating’ turbulence recently found in minimal channel flow by Xi and Graham. All of these observations suggest that an important role for viscoelasticity in the turbulent drag reduction phenomenon, at least near solid surfaces, is to suppress conventional turbulence, while leaving behind a much weaker form of turbulence that can persist for a substantial length of time (or downstream distance) even in the absence of viscoelastic stresses.

JFM classification

Flow Control: Drag reduction Non-Newtonian Flows: Polymers Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 352 - 377
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Benzi, R., De angelis, E. & L’vov, V. S. 2006 Maximum drag reduction asymptotes and the cross-over to the Newtonian plug. J. Fluid Mech. 551, 185–195.CrossRefGoogle Scholar
2. Bird, R. B., Armstrong, R. C. & Hassager, O. 1987a Dynamics of Polymeric Liquids. Volume 1: Fluid Mechanics, 2nd edn. Wiley.Google Scholar
3. Bird, R. B., Armstrong, R. C. & Hassager, O. 1987b Dynamics of Polymeric Liquids. Volume 2: Kinetic Theory, 2nd edn. Wiley.Google Scholar
4. Coles, D. E. 1962 A manual of experimental boundary-layer practice for low-speed flow. Rand Report, No. R-403-PR, The Rand Corp., Santa Monica, CA.Google Scholar
5. De Angelis, E., Casciola, C. M. & Piva, R. 2002 DNS of wall turbulence: dilute polymers and self-sustaining mechanisms. Comput. Fluids 31, 495–507.CrossRefGoogle Scholar
6. Dimitropoulos, C. D., Dubief, Y., Shaqfeh, E. S. G. & Moin, P. 2006 Direct numerical simulation of polymer-induced drag reduction in turbulent boundary layer flow of inhomogeneous polymer solutions. J. Fluid Mech. 566, 153–162.CrossRefGoogle Scholar
7. Dimitropoulos, C. D., Dubief, Y., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2005 Direct numerical simulation of polymer-induced drag reduction in turbulent boundary layer flow. Phys. Fluids 17, 011705.CrossRefGoogle Scholar
8. Dimitropoulos, C. D., Sureshkumar, R. & Beris, A. N. 1998 Direct numerical simulation of viscoelastic turbulent channel flow exhibiting drag reduction: effect of the variation of rheological parameters. J. Non-Newtonian Fluid Mech. 79, 433–468.CrossRefGoogle Scholar
9. Dubief, Y., Terrapon, V., White, C. M., Shaqreh, E. G., Moin, P. & Lele, S. K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74, 311–329.CrossRefGoogle Scholar
10. Dubief, Y., White, C. M., Terrapon, V. E., Shaqfeh, E. S. G., Moin, P. & Lele, S. K. 2004 On the coherent drag-reducing and turbulence-enhancing behaviour of polymers in wall flows. J. Fluid Mech. 514, 271–280.CrossRefGoogle Scholar
11. Dubief, Y., White, C. M., Shaqfeh, E. S. G. & Terrapon, V. E. 2011 Polymer maximum drag reduction: a unique transitional state. Center for Turbulence Research Annual Research Briefs 2010 47–56.Google Scholar
12. Dukowicz, J. K. & Dvinsky, A. S. 1992 Approximate factorization as a high order splitting for the implicit incompressible flow equations. J. Comput. Phys. 102, 336–347.CrossRefGoogle Scholar
13. Hou, Y., Somandepalli, V. S. R. & Mungal, M. G. 2008 Streamwise development of turbulent boundary-layer drag reduction with polymer injection. J. Fluid Mech. 597, 31–66.CrossRefGoogle Scholar
14. Housiadas, K. D. & Beris, A. N. 2004 An efficient fully implicit spectral scheme for DNS of turbulent viscoelastic channel flow. J. Non-Newtonian Fluid Mech. 122, 243–262.CrossRefGoogle Scholar
15. Itoh, M., Tamano, S., Yokota, K. & Ninagawa, M. 2005 Velocity measurement in turbulent boundary layer of drag-reducing surfactant solution. Phys. Fluids 17, 075107.CrossRefGoogle Scholar
16. Kawaguchi, Y., Segawa, T., Feng, Z. & Li, P. 2002 Experimental study on drag-reducing channel flow with surfactant additives–spatial structure of turbulence investigated by PIV system. Intl J. Heat Fluid Flow 23, 700–709.CrossRefGoogle Scholar
17. Kim, K., Adrian, R. J., Balachandar, S. & Sureshkumar, R. 2008 Dynamics of hairpin vortices and polymer-induced turbulent drag reduction. Phys. Rev. Lett. 100, 134504.CrossRefGoogle Scholar
18. Kim, K., Li, C.-F., Sureshkumar, R., Balachandar, S. & Adrian, R. J. 2007 Effects of polymer stresses on eddy structures in drag-reduced turbulent channel flow. J. Fluid Mech. 584, 281–299.CrossRefGoogle Scholar
19. Li, C.-F., Sureshkumar, R. & Khomami, B. 2006 Influence of rheological parameters on polymer induced turbulent drag reduction. J. Non-Newtonian Fluid Mech. 140, 23–40.CrossRefGoogle Scholar
20. Li, W. & Graham, M. D. 2007 Polymer induced drag reduction in exact coherent structures of plane Poiseuille flow. Phys. Fluids 19, 083101.CrossRefGoogle Scholar
21. Lund, T. S., Wu, X. & Squires, K. D. 1998 Generation of turbulent inflow data for spatially-developing boundary layer simulations. J. Comput. Phys. 140, 233–258.CrossRefGoogle Scholar
22. Min, T., Yoo, J. Y. & Choi, H. 2001 Effect of spatial discretization schemes on numerical solutions of viscoelastic fluid flows. J. Non-Newtonian Fluid Mech. 100, 27–47.CrossRefGoogle Scholar
23. Procaccia, I., L’vov, V. S. & Benzi, R. 2008 Colloquium: theory of drag reduction by polymers in wall-bounded turbulence. Rev. Mod. Phys. 80, 225–247.CrossRefGoogle Scholar
24. Ptasinski, P. K., Boersma, B. J., Nieuwstadt, F. T. M., Hulsen, M. A., Van den Brule, B. H. A. A. & Hunt, J. C. R. 2003 Turbulent channel flow near maximum drag reduction: simulations, experiments and mechanisms. J. Fluid Mech. 490, 251–291.CrossRefGoogle Scholar
25. Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
26. Spalart, P. R. 1988 Direct simulation of a turbulent boundary layer up to Re θ = 1410. J. Fluid Mech. 187, 61–98.CrossRefGoogle Scholar
27. Sreenivasan, K. R. & White, C. M. 2000 The onset of drag reduction by dilute polymer additives, and the maximum drag reduction asymptote. J. Fluid Mech. 409, 149–164.CrossRefGoogle Scholar
28. Stone, P. A., Roy, A., Larson, R. G., Waleffe, F. & Graham, M. D. 2004 Polymer drag reduction in exact coherent structures of plane shear flow. Phys. Fluids 16, 3470–3482.CrossRefGoogle Scholar
29. Stone, P. A., Waleffe, W. & Graham, M. D. 2002 Toward a structural understanding of turbulent drag reduction: nonlinear coherent states in viscoelastic shear flow. Phys. Rev. Lett. 89, 208301.CrossRefGoogle Scholar
30. Sureshkumar, R. & Beris, A. N. 1995 Effect of artificial stress diffusivity on the stability of numerical calculations and the flow dynamics of time-dependent viscoelastic flows. J. Non-Newtonian Fluid Mech. 60, 53–80.CrossRefGoogle Scholar
31. Sureshkumar, R., Beris, A. N. & Handler, R. A. 1997 Direct numerical simulation of the turbulent channel flow of a polymer solution. Phys. Fluids 9, 743–755.CrossRefGoogle Scholar
32. Tamano, S., Itoh, M., Hoshizaki, K. & Yokota, K. 2007 Direct numerical simulation on the drag-reducing turbulent boundary layer of viscoelastic fluid. Phys. Fluids 19, 075106.CrossRefGoogle Scholar
33. Tamano, S., Itoh, M., Hotta, S., Yokota, K. & Morinishi, Y. 2009a Effect of rheological properties on drag reduction in turbulent boundary layer flow. Phys. Fluids 21, 055101.CrossRefGoogle Scholar
34. Tamano, S., Itoh, M., Inoue, T., Kato, K. & Yokota, K. 2009b Turbulence statistics and structures of drag-reducing turbulent boundary layer in homogenous aqueous surfactant solutions. Phys. Fluids 21, 045101.CrossRefGoogle Scholar
35. Tamano, S., Itoh, M., Kato, K. & Yokota, K. 2010 Turbulent drag reduction in nonionic surfactant solutions. Phys. Fluids 22, 055102.CrossRefGoogle Scholar
36. Van Der Vorst, H. A. 1992 Bi-CGSTAB: a fast and smoothly converging variant of BiCG for the solution of nonsymmetric linear systems. SIAM J. Sci. Stat. Comput. 13, 631–644.CrossRefGoogle Scholar
37. Virk, P. S. 1975 Drag reduction fundamentals. AIChE J. 21 (4), 625–656.CrossRefGoogle Scholar
38. Warholic, M. D., Massah, H. & Hanratty, T. J. 1999a Influence of drag-reducing polymers on turbulence: effect of Reynolds number, concentration and mixing. Exp. Fluids 27, 461–472.CrossRefGoogle Scholar
39. Warholic, M. D., Schmidt, G. M. & Hanratty, T. J. 1999b The influence of a drag-reducing surfactant on a turbulent velocity field. J. Fluid Mech. 388, 1–20.CrossRefGoogle Scholar
40. White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.CrossRefGoogle Scholar
41. Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient fat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar
42. Xi, L. & Graham, M. D. 2010a Turbulent drag reduction and multistage transitions in viscoelastic minimal flow units. J. Fluid Mech. 647, 421–452.CrossRefGoogle Scholar
43. Xi, L. & Graham, M. D. 2010b Active and hibernating turbulence in minimal channel flow of Newtonian and polymeric fluids. Phys. Rev. Lett. 104, 218301.CrossRefGoogle ScholarPubMed
44. Yu, B. & Kawaguchi, Y. 2003 Effect of Weissenberg number on the flow structure: DNS study of drag-reducing flow with surfactant additives. Intl J. Heat Fluid Flow 24, 491–499.CrossRefGoogle Scholar
45. Yu, B. & Kawaguchi, Y. 2006 Parametric study of surfactant-induced drag-reduction by DNS. Intl J. Heat Fluid Flow 27, 887–894.CrossRefGoogle Scholar