Published online by Cambridge University Press: 25 March 2015
This paper builds upon the investigation of Augier et al. (Phys. Fluids, vol. 26 (4), 2014) in which a strongly stratified turbulent-like flow was forced by 12 generators of vertical columnar dipoles. In experiments, measurements start to provide evidence of the existence of a strongly stratified inertial range that has been predicted for large turbulent buoyancy Reynolds numbers 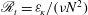 $\mathscr{R}_{t}={\it\varepsilon}_{\!K}/({\it\nu}N^{2})$, where
$\mathscr{R}_{t}={\it\varepsilon}_{\!K}/({\it\nu}N^{2})$, where 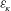 ${\it\varepsilon}_{\!K}$ is the mean dissipation rate of kinetic energy,
${\it\varepsilon}_{\!K}$ is the mean dissipation rate of kinetic energy,  ${\it\nu}$ the viscosity and
${\it\nu}$ the viscosity and 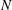 $N$ the Brunt–Väisälä frequency. However, because of experimental constraints, the buoyancy Reynolds number could not be increased to sufficiently large values so that the inertial strongly stratified turbulent range is only incipient. In order to extend the experimental results toward higher buoyancy Reynolds number, we have performed numerical simulations of forced stratified flows. To reproduce the experimental vortex generators, columnar dipoles are periodically produced in spatial space using impulsive horizontal body force at the peripheries of the computational domain. For moderate buoyancy Reynolds number, these numerical simulations are able to reproduce the results obtained in the experiments, validating this particular forcing. For higher buoyancy Reynolds number, the simulations show that the flow becomes turbulent as observed in Brethouwer et al. (J. Fluid Mech., vol. 585, 2007, pp. 343–368). However, the statistically stationary flow is horizontally inhomogeneous because the dipoles are destabilized quite rapidly after their generation. In order to produce horizontally homogeneous turbulence, high-resolution simulations at high buoyancy Reynolds number have been carried out with a slightly modified forcing in which dipoles are forced at random locations in the computational domain. The unidimensional horizontal spectra of kinetic and potential energies scale like
$N$ the Brunt–Väisälä frequency. However, because of experimental constraints, the buoyancy Reynolds number could not be increased to sufficiently large values so that the inertial strongly stratified turbulent range is only incipient. In order to extend the experimental results toward higher buoyancy Reynolds number, we have performed numerical simulations of forced stratified flows. To reproduce the experimental vortex generators, columnar dipoles are periodically produced in spatial space using impulsive horizontal body force at the peripheries of the computational domain. For moderate buoyancy Reynolds number, these numerical simulations are able to reproduce the results obtained in the experiments, validating this particular forcing. For higher buoyancy Reynolds number, the simulations show that the flow becomes turbulent as observed in Brethouwer et al. (J. Fluid Mech., vol. 585, 2007, pp. 343–368). However, the statistically stationary flow is horizontally inhomogeneous because the dipoles are destabilized quite rapidly after their generation. In order to produce horizontally homogeneous turbulence, high-resolution simulations at high buoyancy Reynolds number have been carried out with a slightly modified forcing in which dipoles are forced at random locations in the computational domain. The unidimensional horizontal spectra of kinetic and potential energies scale like 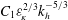 $C_{1}{\it\varepsilon}_{\!K}^{2/3}k_{h}^{-5/3}$ and
$C_{1}{\it\varepsilon}_{\!K}^{2/3}k_{h}^{-5/3}$ and 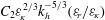 $C_{2}{\it\varepsilon}_{\!K}^{2/3}k_{h}^{-5/3}({\it\varepsilon}_{\!P}/{\it\varepsilon}_{\!K})$, respectively, with
$C_{2}{\it\varepsilon}_{\!K}^{2/3}k_{h}^{-5/3}({\it\varepsilon}_{\!P}/{\it\varepsilon}_{\!K})$, respectively, with 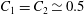 $C_{1}=C_{2}\simeq 0.5$ as obtained by Lindborg (J. Fluid Mech., vol. 550, 2006, pp. 207–242). However, there is a depletion in the horizontal kinetic energy spectrum for scales between the integral length scale and the buoyancy length scale and an anomalous energy excess around the buoyancy length scale probably due to direct transfers from large horizontal scale to small scales resulting from the shear and gravitational instabilities. The horizontal buoyancy flux co-spectrum increases abruptly at the buoyancy scale corroborating the presence of overturnings. Remarkably, the vertical kinetic energy spectrum exhibits a transition at the Ozmidov length scale from a steep spectrum scaling like
$C_{1}=C_{2}\simeq 0.5$ as obtained by Lindborg (J. Fluid Mech., vol. 550, 2006, pp. 207–242). However, there is a depletion in the horizontal kinetic energy spectrum for scales between the integral length scale and the buoyancy length scale and an anomalous energy excess around the buoyancy length scale probably due to direct transfers from large horizontal scale to small scales resulting from the shear and gravitational instabilities. The horizontal buoyancy flux co-spectrum increases abruptly at the buoyancy scale corroborating the presence of overturnings. Remarkably, the vertical kinetic energy spectrum exhibits a transition at the Ozmidov length scale from a steep spectrum scaling like 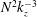 $N^{2}k_{z}^{-3}$ at large scales to a spectrum scaling like
$N^{2}k_{z}^{-3}$ at large scales to a spectrum scaling like 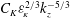 $C_{K}{\it\varepsilon}_{\!K}^{2/3}k_{z}^{-5/3}$, with
$C_{K}{\it\varepsilon}_{\!K}^{2/3}k_{z}^{-5/3}$, with 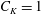 $C_{K}=1$, the classical Kolmogorov constant.
$C_{K}=1$, the classical Kolmogorov constant.