Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-29T19:45:37.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic analysis of steady seepage underneath a water-retaining wall through highly anisotropic porous media

Published online by Cambridge University Press:  30 July 2015

G. Severino  and
S. De Bartolo
G. Severino
Affiliation:
Division of Water Resources Management, University of Naples Federico II, Italy
S. De Bartolo
Affiliation:
Department of Civil Engineering, University of Calabria, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

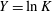Steady seepage is determined by a head drop upstream/downstream of a water-retaining wall. Due to its erratic variations, hydraulic log-conductivity $Y=\ln K$ is modelled as a stationary random space function (RSF). We deal with a highly anisotropic porous formation, i.e. an axisymmetric medium where the horizontal correlation integral scale of 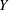$Y$ is much larger than the vertical one. The goal of computing the resulting flow field within a stochastic framework is complicated by non-uniformity of the mean flow. Simple (closed-form) expressions for the correlation functions of the flow variables as well as the mean head are derived. We use these results to quantify the impact of spatial variability of $Y$ upon the probability that the exit volumetric flow rate downstream of the wall is greater than that obtained by regarding the formation as homogeneous (with constant hydraulic conductivity). In particular, we show that the spatial variability of 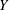$Y$ may lead to predictions (and consequently to design choices) which significantly differ from those achieved by regarding the porous formation as homogeneous.

JFM classification

Mathematical Foundations: General fluid mechanics Waves/Free-surface Flows: Hydraulics Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 253 - 272
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bruggeman, G. A. 1999 Analytical Solutions of Geohydrological Problems. Elsevier.Google Scholar
Dagan, G. 1987 Theory of solute transport by groundwater. Annu. Rev. Fluid Mech. 19, 183–215.CrossRefGoogle Scholar
Dagan, G. 1989 Flow and Transport in Porous Formation. Springer.CrossRefGoogle Scholar
Fenton, G. A. & Griffiths, D. V. 2008 Risk Assessment in Geotechnical Engineering. Wiley.CrossRefGoogle Scholar
Ferrari, A., Fraccarollo, L., Dumbser, M., Toro, E. F. & Armanini, A. 2010 Three-dimensional flow evolution after a dam break. J. Fluid Mech. 663, 456–477.CrossRefGoogle Scholar
Fiori, A., Indelman, P. & Dagan, G. 1998 Correlation structure of flow variables for steady flow toward a well with application to highly anisotropic heterogeneous formations. Water Resour. Res. 34 (4), 699–708.CrossRefGoogle Scholar
Fraccarollo, L. & Capart, H. 2002 Riemann wave description of erosional dam-break flows. J. Fluid Mech. 461, 183–228.CrossRefGoogle Scholar
Griffiths, D. V. & Fenton, A. G. 1997 Three-dimensional seepage through spatially random soil. J. Geotech. Geoenviron. Engng 123 (2), 153–160.CrossRefGoogle Scholar
Griffiths, D. V. & Fenton, G. A. 2007 Probabilistic Methods in Geotechnical Engineering. Springer.CrossRefGoogle Scholar
Guadagnini, A., Guadagnini, L., Tartakovsky, D. M. & Winter, L. 2003 Random domain decomposition for flow in heterogeneous stratified aquifers. Stoch. Environ. Res. Risk Assess. 17 (2), 394–407.CrossRefGoogle Scholar
Indelman, P. 1996 Averaging of unsteady flows in heterogeneous media of stationary conductivity. J. Fluid Mech. 310, 39–60.CrossRefGoogle Scholar
Indelman, P. & Dagan, G. 1999 Solute transport in divergent radial flow through heterogeneous porous media. J. Fluid Mech. 384, 159–182.CrossRefGoogle Scholar
Indelman, P., Or, D. & Rubin, Y. 1993 Stochastic analysis of unsaturated steady state flow through bounded heterogeneous formations. Water Resour. Res. 29 (4), 1141–1148.CrossRefGoogle Scholar
Lancellotta, R. 1993 Geotechnical Engineering. A. A. Balkema.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid Mechanics. Pergamon.Google Scholar
Pope, S. B. 2010 Turbulent Flows. Cambridge University Press.Google Scholar
Rubin, Y. 2003 Applied Sthocastic Hydrogeology. Oxford University Press.CrossRefGoogle Scholar
Severino, G. 2011 Stochastic analysis of well-type flows in randomly heterogeneous porous formations. Water Resour. Res. 47 (3), W03520.CrossRefGoogle Scholar
Severino, G. & Coppola, A. 2012 A note on the apparent conductivity of stratified porous media in unsaturated steady flow above a water table. Transp. Porous Media 91 (2), 733–740.CrossRefGoogle Scholar
Severino, G., Santini, A. & Sommella, A. 2008 Steady flows driven by sources of random strength in heterogeneous aquifers with application to partially penetrating wells. Stoch. Environ. Res. Risk Assess. 22, 567–582.CrossRefGoogle Scholar
Sudicky, E. A. 1986 A natural gradient experiment on solute transport in a sand aquifer: spatial variability of hydraulic conductivity and its role in the dispersion process. Water Resour. Res. 22 (13), 2069–2082.CrossRefGoogle Scholar
Tartakovsky, D. M. 2013 Assessment and management of risk in subsurface hydrology: A review and perspective. Adv. Water Resour. 51, 247–260.CrossRefGoogle Scholar
Tartakovsky, D. M., Guadagnini, A. & Riva, M. 2003 Stochastic averaging of nonlinear flows in heterogeneous porous media. J. Fluid Mech. 492, 47–62.CrossRefGoogle Scholar
Zinn, B. & Harvey, C. 2003 When good statistical models of aquifer heterogeneity go bad: a comparison of flow, dispersion, and mass transfer in connected and multivariate gaussian hydraulic conductivity fields. Water Resour. Res. 39 (3), 1051.CrossRefGoogle Scholar