Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-03T01:03:20.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistics and structure of spanwise rotating turbulent channel flow at moderate Reynolds numbers

Published online by Cambridge University Press:  04 September 2017

Geert Brethouwer Open the ORCID record for Geert Brethouwer [Opens in a new window]
Geert Brethouwer*
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A study of fully developed plane turbulent channel flow subject to spanwise system rotation through direct numerical simulations is presented. In order to study both the influence of the Reynolds number and spanwise rotation on channel flow, the Reynolds number 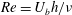$Re=U_{b}h/\unicode[STIX]{x1D708}$ is varied from a low 3000 to a moderate 31 600 and the rotation number 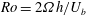$Ro=2\unicode[STIX]{x1D6FA}h/U_{b}$ is varied from 0 to 2.7, where 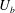$U_{b}$ is the mean bulk velocity, 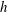$h$ the channel half-gap, $\unicode[STIX]{x1D708}$ the viscosity and 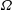$\unicode[STIX]{x1D6FA}$ the system rotation rate. The mean streamwise velocity profile displays also at higher 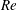$Re$ a characteristic linear part with a slope near to 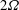$2\unicode[STIX]{x1D6FA}$, and a corresponding linear part in the profiles of the production and dissipation rate of turbulent kinetic energy appears. With increasing 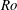$Ro$, a distinct unstable side with large spanwise and wall-normal Reynolds stresses and a stable side with much weaker turbulence develops in the channel. The flow starts to relaminarize on the stable side of the channel and persisting turbulent–laminar patterns appear at higher 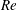$Re$. If 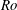$Ro$ is further increased, the flow on the stable side becomes laminar-like while at yet higher 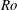$Ro$ the whole flow relaminarizes, although the calm periods might be disrupted by repeating bursts of turbulence, as explained by Brethouwer (Phys. Rev. Fluids, vol. 1, 2016, 054404). The influence of the Reynolds number is considerable, in particular on the stable side of the channel where velocity fluctuations are stronger and the flow relaminarizes less quickly at higher 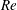$Re$. Visualizations and statistics show that, at 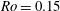$Ro=0.15$ and 0.45, large-scale structures and large counter-rotating streamwise roll cells develop on the unstable side. These become less noticeable and eventually vanish when 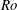$Ro$ rises, especially at higher 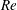$Re$. At high 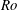$Ro$, the largest energetic structures are larger at lower 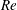$Re$.

JFM classification

Turbulent Flows: Rotating turbulence Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 828 , 10 October 2017 , pp. 424 - 458
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.Google Scholar
Agostini, L. & Leschziner, M. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28, 015107.CrossRefGoogle Scholar
Alvelius, K.1999 Studies of turbulence and its modelling through large eddy- and direct numerical simulations. PhD thesis, Department of Mechanics, KTH, Stockholm, Sweden.Google Scholar
Arolla, S. K. & Durbin, P. A. 2013 Modeling rotation and curvature effects within scalar eddy viscosity model framework. Intl J. Heat Fluid Flow 39, 78–89.CrossRefGoogle Scholar
Barkley, D. & Tuckerman, L. S. 2007 Mean flow of turbulent–laminar patterns in plane Couette flow. J. Fluid Mech. 576, 109–137.Google Scholar
Brethouwer, G. 2005 The effect of rotation on rapidly sheared homogeneous turbulence and passive scalar transport. Linear theory and direct numerical simulations. J. Fluid Mech. 542, 305–342.Google Scholar
Brethouwer, G. 2016 Linear instabilities and recurring bursts of turbulence in rotating channel flow simulations. Phys. Rev. Fluids 1, 054404.Google Scholar
Brethouwer, G., Duguet, Y. & Schlatter, P. 2012 Turbulent–laminar coexistence in wall flows with Coriolis, buoyancy or Lorentz forces. J. Fluid Mech. 704, 137–172.Google Scholar
Brethouwer, G., Schlatter, P., Duguet, Y., Henningson, D. H. & Johansson, A. V. 2014 Recurrent bursts via linear processes in turbulent environments. Phys. Rev. Lett. 112, 144502.Google Scholar
Chevalier, M., Schlatter, P., Lundbladh, A. & Henningson, D. S.2007 A pseudo-spectral solver for incompressible boundary layer flows. Tech. Rep., TRITA-MEK 2007:07, KTH Mechanics, Stockholm, Sweden.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Dai, Y.-J., Huang, W.-X. & Xu, C.-X. 2016 Effects of Taylor–Görtler vortices on turbulent flows in a spanwise-rotating channel. Phys. Fluids 28, 115104.Google Scholar
Deusebio, E., Brethouwer, G., Schlatter, P. & Lindborg, E. 2014 A numerical study of the stratified and unstratified Ekman layer. J. Fluid Mech. 755, 672–704.Google Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane Couette flow. J. Fluid Mech. 781, 298–329.Google Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110, 034502.Google Scholar
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.Google Scholar
Gai, J., Xia, Z., Cai, Q. & Chen, S. 2016 Turbulent statistics and flow structures in spanwise-rotating turbulent plane Couette flows. Phys. Rev. Fluids 1, 054401.Google Scholar
Garcia-Villalba, M. & del Álamo, J. C. 2011 Turbulence modification by stable stratification in channel flow. Phys. Fluids 23, 045104.Google Scholar
Grundestam, O., Wallin, S. & Johansson, A. V. 2008 Direct numerical simulations of rotating turbulent channel flow. J. Fluid Mech. 598, 177–199.CrossRefGoogle Scholar
Hamba, F. 2006 The mechanism of zero absolute vorticity state in rotating channel flow. Phys. Fluids 18, 125104.Google Scholar
Hsieh, A. & Biringen, S. 2016 The minimal flow unit in complex turbulent flows. Phys. Fluids 28, 125102.Google Scholar
Hsieh, A., Biringen, S. & Kucala, A. 2016 Simulation of rotating channel flow with heat transfer: evaluation of closure models. Trans. ASME J. Turbomach. 138, 111009.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Iida, O., Fukudome, K., Iwata, T. & Nagano, Y. 2010 Low Reynolds number effects on rotating turbulent Poiseuille flow. Phys. Fluids 22, 085106.Google Scholar
Jakirlić, S., Hanjalić, K. & Tropea, C. 2002 Modeling rotating and swirling turbulent flows: a perpetual challenge. AIAA J. 40, 1984–1996.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–559.Google Scholar
Kawata, T. & Alfredsson, P. H. 2016 Experiments in rotating plane Couette flow – momentum transport by coherent roll-cell structure and zero-absolute-vorticity state. J. Fluid Mech. 791, 191–213.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds number turbulent flow in a rotating channel. J. Fluid Mech. 256, 163–197.CrossRefGoogle Scholar
Lamballais, E., Lesieur, M. & Métais, O. 1996 Effects of spanwise rotation on the vorticity stretching in transitional and turbulent channel flow. Intl J. Heat Fluid Flow 17, 324–332.Google Scholar
Lamballais, E., Métais, O. & Lesieur, M. 1998 Spectral-dynamic model for large-eddy simulations of turbulent rotating channel flow. Theor. Comput. Fluid Dyn. 12, 149–177.Google Scholar
Lee, M. & Moser, R. D. 2015 Direct numerical simulation of turbulent channel flow up to Re 𝜏 ≈ 5200. J. Fluid Mech. 774, 395–415.Google Scholar
Lenaers, P., Li, Q., Brethouwer, G., Schlatter, P. & Örlü, R. 2012 Rare backflow and extreme wall-normal velocity fluctuations in near-wall turbulence. Phys. Fluids 24, 035110.Google Scholar
Liu, N.-S. & Lu, X.-Y. 2007 Direct numerical simulation of spanwise rotating turbulent channel flow with heat transfer. Intl J. Numer. Meth. Fluids 53, 1689–1706.Google Scholar
Marstorp, L., Brethouwer, G., Grundestam, O. & Johansson, A. V. 2009 Explicit algebraic subgrid stress models with application to rotating channel flow. J. Fluid Mech. 639, 403–432.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Nagano, Y. & Hattori, H. 2003 Direct numerical simulation and modelling of spanwise rotating channel flow with heat transfer. J. Turbul. 4, 010.Google Scholar
Nakabayashi, K. & Kitoh, O. 2005 Turbulence characteristics of two-dimensional channel flow with system rotation. J. Fluid Mech. 528, 355–377.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Salhi, A. & Cambon, C. 1997 An analysis of rotating shear flow using linear theory and DNS and LES results. J. Fluid Mech. 347, 171–195.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows, Applied Mathematical Sciences, vol. 142. Springer.Google Scholar
Smirnov, P. E. & Menter, F. R. 2009 Sensitization of the SST turbulence model to rotation and curvature by applying the Spalart–Shur correction. Trans. ASME J. Turbomach. 131, 041010.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Tritton, D. J. 1992 Stabilization and destablization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.Google Scholar
Tuckerman, L. S., Kreilos, T., Schrobsdorff, H., Schneider, T. M. & Gibson, J. F. 2014 Turbulent–laminar patterns in plane Poiseuille flow. Phys. Fluids 26, 114103.Google Scholar
Wall, D. P. & Nagata, M. 2013 Three-dimensional exact coherent states in rotating channel flow. J. Fluid Mech. 727, 533–581.Google Scholar
Wallin, S., Grundestam, O. & Johansson, A. V. 2013 Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow. J. Fluid Mech. 730, 193–219.Google Scholar
Xia, Z., Shi, Y. & Chen, S. 2016 Direct numerical of turbulent channel flow with spanwise rotation. J. Fluid Mech. 788, 42–56.CrossRefGoogle Scholar
Yang, Z. X., Cui, G. X., Zhang, Z. S. & Xu, C. X. 2012 A modified nonlinear sub-grid scale model for large eddy simulation with application to rotating turbulent channel flows. Phys. Fluids 24, 075113.Google Scholar
Yang, Y.-T. & Wu, J.-Z. 2012 Channel turbulence with spanwise rotation studied using helical wave decomposition. J. Fluid Mech. 692, 137–152.Google Scholar