Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-17T17:14:33.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical signatures of 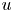$u$ component wall-attached eddies in proper orthogonal decomposition modes of a turbulent boundary layer

Published online by Cambridge University Press:  29 June 2022

Longwei Wang Open the ORCID record for Longwei Wang [Opens in a new window] ,
Chong Pan Open the ORCID record for Chong Pan [Opens in a new window] ,
Jinjun Wang Open the ORCID record for Jinjun Wang [Opens in a new window]  and
Qi Gao Open the ORCID record for Qi Gao [Opens in a new window]
Longwei Wang
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beihang University, Beijing 100191, PR China
Chong Pan*
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beihang University, Beijing 100191, PR China Aircraft and Propulsion Laboratory, Ningbo Institute of Technology, Beihang University, Ningbo 315800, PR China
Jinjun Wang
Affiliation:
Fluid Mechanics Key Laboratory of Education Ministry, Beihang University, Beijing 100191, PR China
Qi Gao
Affiliation:
School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Physical representation of coherent motions in wall-bounded turbulence satisfying Townsend's attached-eddy hypothesis (AEH) is still an open question to be debated. 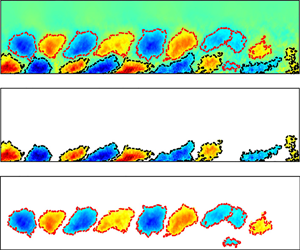Here, we apply proper orthogonal decomposition (POD) to instantaneous snapshots of $u$ component velocity fields in the streamwise–wall-normal plane of three turbulent boundary layers, which cover a frictional Reynolds number ($Re$) of $Re_\tau \approx 1000{\sim} 4000$ and were either measured by large-field-of-view planar particle image velocimetry or calculated by direct numerical simulation. The $u$ component POD modes characterized by streamwise recurring large-scale motions are decomposed into wall-attached and wall-detached parts depending on the wall-attachment condition. The former, i.e. wall-attached POD eddies, are believed to be the prime statistical representations of attached eddies. The reason lies in three aspects. Firstly, wall-attached POD eddies are geometrically self-similar and statistically independent. Secondly, the wall-normal variation of the variance of reduced-order streamwise velocity components $\tilde {u}_{AE}$, which is only contributed by wall-attached POD eddies, presents logarithmic decay in the inertial flow region. Thirdly, analysis on the scaling behaviour of the high-even-order moment, moment generating function, as well as longitudinal two-point structure function, all indicate a quasi-Gaussian behaviour of $\tilde {u}_{AE}$. None of these AEH-predicted behaviours are evident when the contribution of superstructure-like POD eddies are considered. Furthermore, wall-detached POD eddies are found to also present quasi-Gaussian behaviour. They might be treated as passive fragments of wall-attached ones.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 944 , 10 August 2022 , A26
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Agostini, L. & Leschziner, M. 2016 Predicting the response of small-scale near-wall turbulence to large-scale outer motions. Phys. Fluids 28 (1), 015107.CrossRefGoogle Scholar
Baars, W.J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 a Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 1. Energy spectra. J. Fluid Mech. 882, A25.CrossRefGoogle Scholar
Baars, W.J. & Marusic, I. 2020 b Data-driven decomposition of the streamwise turbulence kinetic energy in boundary layers. Part 2. Integrated energy and $A_1$. J. Fluid Mech. 882, A26.CrossRefGoogle Scholar
Baidya, R., et al. 2019 Simultaneous skin friction and velocity measurements in high reynolds number pipe and boundary layer flows. J. Fluid Mech. 871, 377–400.CrossRefGoogle Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J.P. & Marusic, I. 2017 Distance-from-the-wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.CrossRefGoogle Scholar
Balakumar, B.J. & Adrian, R.J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. A Math. Phys. Engng 365 (1852), 665–681.Google ScholarPubMed
Benzi, R., Ciliberto, S., Tripiccione, R., Baudet, C., Massaioli, F. & Succi, S. 1993 Extended self-similarity in turbulent flows. Phys. Rev. E, Stat. Phys. Plasmas Fluids Related Interdisciplinary Topics 48, R29–R32.Google ScholarPubMed
Berkooz, G., Holmes, P. & Lumley, J.L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Borrell, G., Sillero, J. & Jiménez, J. 2013 A code for direct numerical simulation of turbulent boundary layers at high reynolds numbers in bg/p supercomputers. Comput. Fluids 80, 37–43.CrossRefGoogle Scholar
Carter, D. & Coletti, F. 2017 Scale-to-scale anisotropy in homogeneous turbulence. J. Fluid Mech. 827, 250–284.CrossRefGoogle Scholar
Chandran, D., Baidya, R., Monty, J. & Marusic, I. 2017 Two-dimensional energy spectra in high Reynolds number turbulent boundary layers. J. Fluid Mech. 826, R1.CrossRefGoogle Scholar
Chandran, D., Monty, J.P. & Marusic, I. 2020 Spectral-scaling-based extension to the attached eddy model of wall turbulence. Phys. Rev. Fluids 5, 104606.CrossRefGoogle Scholar
Chauhan, K.A., Monkewitz, P.A. & Nagib, H.M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 328–332.CrossRefGoogle Scholar
Cheng, C., Li, W., Lozano-Durán, A. & Liu, H. 2019 Identity of attached eddies in turbulent channel flows with bidimensional empirical mode decomposition. J. Fluid Mech. 870, 1037–1071.CrossRefGoogle ScholarPubMed
Cheng, C., Li, W., Lozano-Durán, A. & Liu, H. 2020 Uncovering townsend's wall-attached eddies in low-Reynolds-number wall turbulence. J. Fluid Mech. 889, A29.CrossRefGoogle Scholar
Del Alamo, J.C. & Zandonade, P. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Deng, S., Pan, C., Wang, J. & He, G. 2018 On the spatial organization of hairpin packets in a turbulent boundary layer at low-to-moderate Reynolds number. J. Fluid Mech. 844, 635–668.CrossRefGoogle Scholar
Dennis, D.J.C. & Nickels, T.B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.CrossRefGoogle Scholar
Deshpande, R., Chandran, D., Monty, J. & Marusic, I. 2020 Two-dimensional cross-spectrum of the streamwise velocity in turbulent boundary layers. J. Fluid Mech. 890, R2.CrossRefGoogle Scholar
Deshpande, R., Monty, J.P. & Marusic, I. 2019 Streamwise inclination angle of large wall-attached structures in turbulent boundary layers. J. Fluid Mech. 877, R4.CrossRefGoogle Scholar
Deshpande, R., Monty, J.P. & Marusic, I. 2021 a Active and inactive components of the streamwise velocity in wall-bounded turbulence. J. Fluid Mech. 914, A5.CrossRefGoogle Scholar
Deshpande, R., de Silva, C.M., Lee, M., Monty, J.P. & Marusic, I. 2021 b Data-driven enhancement of coherent structure-based models for predicting instantaneous wall turbulence. Intl J. Heat Fluid Flow 92, 108879.CrossRefGoogle Scholar
Duggleby, A., Ball, K., Paul, M. & Fischer, P. 2006 Dynamical eigenfunction decomposition of turbulent pipe flow. J. Turbul. 8, N43.CrossRefGoogle Scholar
Eich, F., de Silva, C.M., Marusic, I. & Kähler, C.J. 2020 Towards an improved spatial representation of a boundary layer from the attached eddy model. Phys. Rev. Fluids 5 (3), 034601.CrossRefGoogle Scholar
Ganapathisubramani, B. & Longmire, E.K. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478 (478), 35–46.CrossRefGoogle Scholar
Hamilton, J.M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287 (-1), 317–348.CrossRefGoogle Scholar
Hellström, L., Ganapathisubramani, B. & Smits, A. 2015 The evolution of large-scale motions in turbulent pipe flow. J. Fluid Mech. 779, 701–715.CrossRefGoogle Scholar
Hellström, L.H.O., Marusic, I. & Smits, A.J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.CrossRefGoogle Scholar
Herpin, S., Stanislas, M., Foucaut, J.-M. & Coudert, S. 2013 Influence of the reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.CrossRefGoogle Scholar
Hu, R., Yang, X.I.A. & Zheng, X. 2020 Wall-attached and wall-detached eddies in wall-bounded turbulent flows. J. Fluid Mech. 885, A30.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.CrossRefGoogle Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.CrossRefGoogle Scholar
Hwang, J. & Lee, J. 2020 a Statistical behaviour of self-similar structures in canonical wall turbulence. J. Fluid Mech. 905, A6.CrossRefGoogle Scholar
Hwang, Y. & Lee, M. 2020 b The mean logarithm emerges with self-similar energy balance. J. Fluid Mech. 903, R6.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2019 Wall-attached clusters for the logarithmic velocity law in turbulent pipe flow. Phys. Fluids 31, 055109.Google Scholar
Jiménez, J. & Hoyas, S. 2008 Turbulent fluctuations above the buffer layer of wall-bounded flows. J. Fluid Mech. 611 (611), 215–236.CrossRefGoogle Scholar
Kolmogorov, A. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds’ numbers. C. R. (Doklady) Acad. Sci. URSS Nouvelle Série 30.Google Scholar
Lee, J.H., Kevin, , Monty, J.P. & Hutchins, N. 2016 Validating under-resolved turbulence intensities for piv experiments in canonical wall-bounded turbulence. Exp. Fluids 57 (8), 129.CrossRefGoogle Scholar
Lozano-Durán, A., Flores, O. & Jiménez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 694, 100–130.CrossRefGoogle Scholar
Lozano-Durán, A. & Jimenez, J. 2014 Time-resolved evolution of coherent structures in turbulent channels: characterization of eddies and cascades. J. Fluid Mech. 759, 432–471.CrossRefGoogle Scholar
Marusic, I. & Monty, J. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51, 49–74.CrossRefGoogle Scholar
Marusic, I., Monty, J.P., Hultmark, M. & Smits, A.J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.CrossRefGoogle Scholar
Meneveau, C. & Marusic, I. 2013 Generalized logarithmic law for high-order moments in turbulent boundary layers. J. Fluid Mech. 719, R1.CrossRefGoogle Scholar
Moin, P. & Moser, R. 1991 Characteristic-eddy decomposition of turbulence in channel. J. Fluid Mech. 200, 471–509.CrossRefGoogle Scholar
Pan, C., Xue, D., Yang, X., Wang, J.J. & Wei, R.J. 2015 Evaluating the accuracy performance of Lucas-Kanade algorithm in the circumstance of PIV application. Sci. China (Phys. Mech. Astron.) 58, 16.Google Scholar
Perry, A.E. & Chong, M.S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119 (1), 173–217.CrossRefGoogle Scholar
Perry, A.E., Henbest, S. & Chong, M.S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165 (1), 163–199.CrossRefGoogle Scholar
Perry, A.E. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2012 Turbulent boundary layers at moderate Reynolds numbers: inflow length and tripping effects. J. Fluid Mech. 710, 5–34.CrossRefGoogle Scholar
She, Z.-S. & Leveque, E. 1994 Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72 (3), 336.CrossRefGoogle ScholarPubMed
Siebert, H., Shaw, R.A. & Warhaft, Z. 2009 Statistics of small-scale velocity fluctuations and internal intermittency in marine stratocumulus clouds. J. Atmos. Sci. 67, 262–273.CrossRefGoogle Scholar
Sillero, J., Jiménez, J. & Moser, R. 2013 One-point statistics for turbulent wall-bounded flows at Reynolds numbers up to $\delta ^{+}{\sim} 2000$. Phys. Fluids 25, 5102.CrossRefGoogle Scholar
de Silva, C., Chandran, D., Hutchins, N. & Marusic, I. 2020 Periodicity of large-scale coherence in turbulent boundary layers. Intl J. Heat Fluid Flow 83, 108575.CrossRefGoogle Scholar
de Silva, C.M., Hutchins, N. & Marusic, I. 2016 a Uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 786, 309–331.CrossRefGoogle Scholar
de Silva, C., Marusic, I., Woodcock, J. & Meneveau, C. 2015 Scaling of second- and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.CrossRefGoogle Scholar
de Silva, C.M., Woodcock, J.D., Hutchins, N. & Marusic, I. 2016 b Influence of spatial exclusion on the statistical behavior of attached eddies. Phys. Rev. Fluids. 1 (2), 022401pRFLUIDSCrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Maths 45, 561–571.CrossRefGoogle Scholar
Smits, A., McKeon, B. & Marusic, I. 2011 High–Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Sreenivasan, R.K. & Antonia, A.R. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29 (1), 435–472.CrossRefGoogle Scholar
Stevens, R.J.A.M., Wilczek, M. & Meneveau, C. 2014 Large-eddy simulation study of the logarithmic law for second- and higher-order moments in turbulent wall-bounded flow. J. Fluid Mech. 757, 888–907.CrossRefGoogle Scholar
Townsend, A.A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (01), 101–149.CrossRefGoogle Scholar
Townsend, A.A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Townsend, A.A. & Batchelor, G.K. 1951 The structure of the turbulent boundary layer. Math. Proc. Camb. Phil. Soc. 47 (2), 375–395.CrossRefGoogle Scholar
Wang, C., Gao, Q., Wang, B., Pan, C. & Wang, J. 2020 Vortex-to-velocity reconstruction for wall-bounded turbulence via a data-driven model. J. Fluid Mech. 922, A18.CrossRefGoogle Scholar
Wang, C., Gao, Q., Wang, B., Pan, C. & Wang, J. 2021 a Vortex-to-velocity reconstruction for wall-bounded turbulence via the field-based linear stochastic estimation. J. Fluid Mech. 922, A18.CrossRefGoogle Scholar
Wang, C., Gao, Q., Wang, J., Wang, B. & Pan, C. 2019 a Experimental study on dominant vortex structures in near-wall region of turbulent boundary layer based on tomographic particle image velocimetry. J. Fluid Mech. 874, 426–454.CrossRefGoogle Scholar
Wang, W., Pan, C. & Wang, J. 2018 Quasi-bivariate variational mode decomposition as a tool of scale analysis in wall-bounded turbulence. Exp. Fluids 59 (1), 1.CrossRefGoogle Scholar
Wang, W., Pan, C. & Wang, J. 2019 b Multi-component variational mode decomposition and its application on wall-bounded turbulence. Exp. Fluids 60 (6), 95.CrossRefGoogle Scholar
Wang, L.-H., Xu, C.-X., Sung, H.J. & Huang, W.-X. 2021 b Wall-attached structures over a traveling wavy boundary: turbulent velocity fluctuations. Phys. Rev. Fluids 6 (3), 034611.CrossRefGoogle Scholar
Woodcock, J.D. & Marusic, I. 2015 The statistical behaviour of attached eddies. Phys. Fluids 27 (1), 97–120.CrossRefGoogle Scholar
Wu, Y. 2014 A study of energetic large-scale structures in turbulent boundary layer. Phys. Fluids 26 (4), 166–178.CrossRefGoogle Scholar
Wu, Y. & Christensen, K. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.CrossRefGoogle Scholar
Wu, Y. & Christensen, K.T. 2006 Population trends of spanwise vortices in wall turbulence. J. Fluid Mech. 568, 55–76.CrossRefGoogle Scholar
Yang, X., Baidya, R., Johnson, P., Marusic, I. & Meneveau, C. 2017 Structure function tensor scaling in the logarithmic region derived from the attached eddy model of wall-bounded turbulent flows. Phys. Rev. Fluids 2, 064602.CrossRefGoogle Scholar
Yang, X.I.A., Marusic, I. & Meneveau, C. 2016 Moment generating functions and scaling laws in the inertial layer of turbulent wall-bounded flows. J. Fluid Mech. 791, R2.CrossRefGoogle Scholar
Yoon, M., Hwang, J. & Yang, J. 2020 Wall-attached structures of streamwise velocity fluctuations in an adverse-pressure-gradient turbulent boundary layer. J. Fluid Mech. 885, A12.CrossRefGoogle Scholar
Zhou, J., Adrian, R.J., Balachandar, S. & Kendall, T.M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar
Zhu, H., Pan, C., Wang, G., Liang, Y., Ji, X. & Wang, J. 2021 Attached eddy-like particle clustering in a turbulent boundary layer under net sedimentation conditions. J. Fluid Mech. 920, A53.CrossRefGoogle Scholar